
Normalizing Inputs

1) substract mean
$$\mu = \frac{1}{m} \sum_{i=1}^{m} x^{(i)}$$
$$x := x - \mu$$
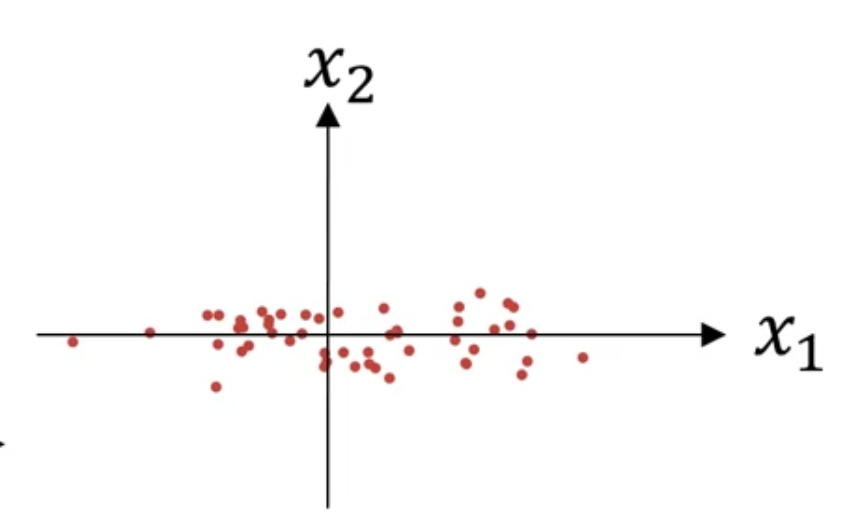
평균이 $0$이 되도록 training set 을 이동시킴
2) normalize variances
위 그래프에서 보면 $x_{2}$에 비해 $x_{1}$가 variance가 더 큼
$$\sigma^{2} = \frac{1}{m} \sum_{i=1}^{m} x^{(i)} \star \star 2$$
- $\star \star 2$ : element-wise squaring
- $\sigma^{2}$ : a vector with the variances of each of the features (평균을 제외한 상태이므로)
$$ x /= \sigma$$
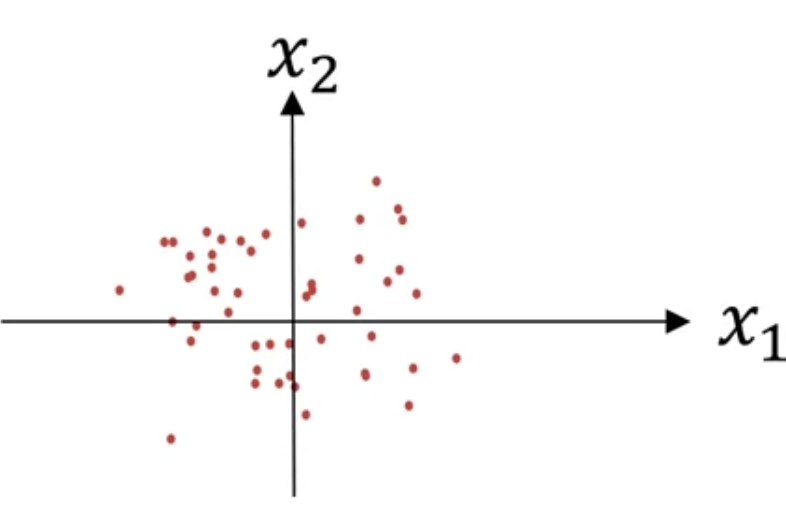
이러한 식으로 training set 을 scaling 했다면, 동일한 $\sigma^{2}$와 $\mu$를 활용해서 test set도 scaling 할 것!!
[Why normalize inputs?]
$$J(w, b) = \frac{1}{m} \sum_{i=1}^{m}L({\hat{y}}^{(i)}, y^{(i)})$$
데이터를 normalize하지 않으면 cost function이 elongated(쭉 늘어진)된 모습을 보임
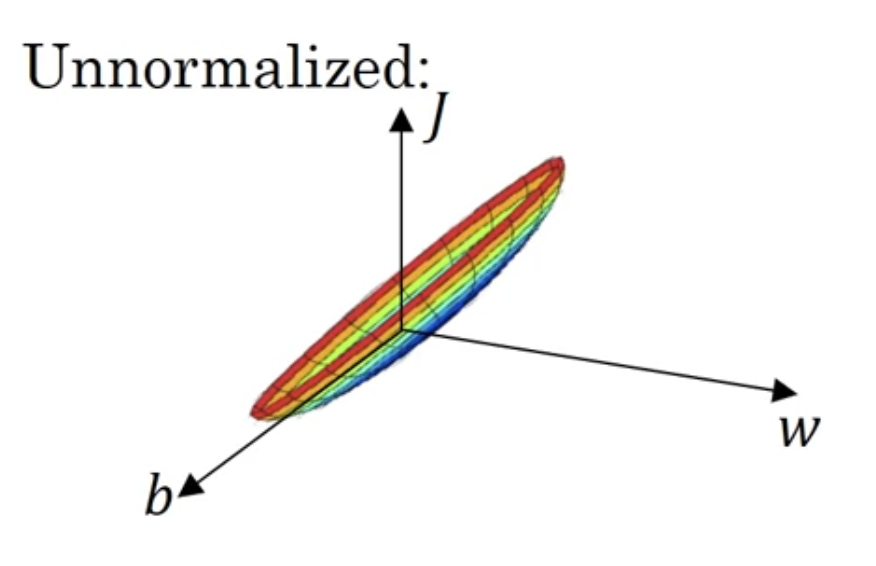

input feature들의 range가 매우 다를 때, $w$들도 매우 다른 값을 가지게 됨
normalize 되었을 때는 훨씬 symmetric한 모습을 확인할 수 있음

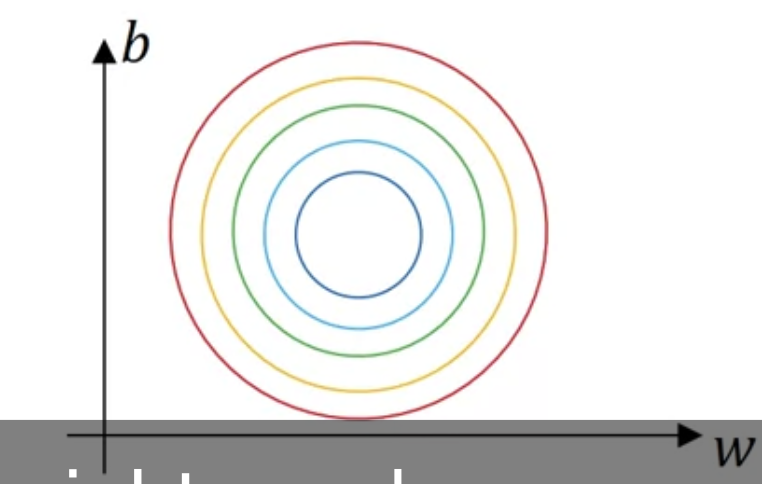
gradient descent 할 때도,

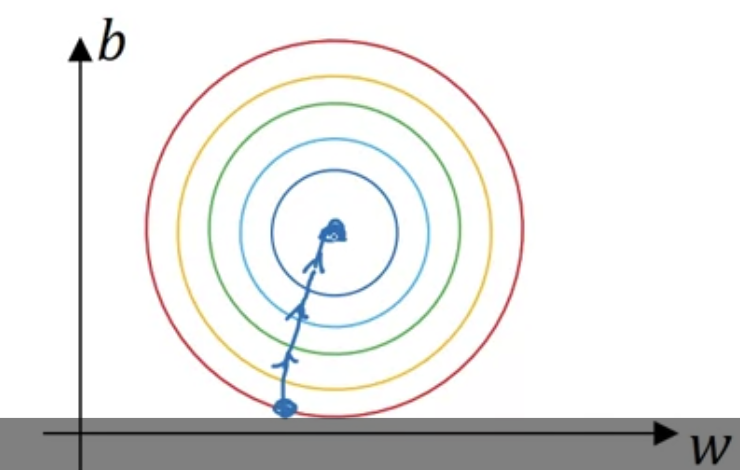
이를 테면, feature 하나는 범위가 1~1000 이고 또다른 하나는 0~1 일 때, range의 차이가 너무 큼 -> 최적화 문제
하지만 normalize 통해 평균을 0으로, 분산을 1로 세팅하면 feature들이 비슷한 스케일이 되고 학습이 빨라짐
Vanishing / Exploding Gradients
깊은 신경망을 훈련할 때 gradient가 너무너무 작거나 너무너무 커지는 문제

위 신경망의 활성화함수 $g(z)$가 linear function으로 $g(z) = z$라고 해보자. 그리고 $b^{[l]}=0$ 로 일단 없는 셈 치기.
$g(z) = z$ 이기 때문에, $z^{[l]} = w^{[l]}a^{[l-1]}$, 그리고 $a^{[l]} = g(z^{[l]})= z^{[l]}$
결국에
$$\hat{y} = w^{[L]}w^{[L-1]}w^{[L-2]} \ldots w^{[3]}w^{[2]}w^{[1]}x$$
이때 $w^{[l]} = \begin{bmatrix} 1.5 & 0 \\ 0 & 1.5 \end{bmatrix}$ 라고 해보자
물론 마지막 $w^{[L]}$는 차원이 다르기 때문에 다시 표현해보자면
$$\hat{y} = w^{[L]}{\begin{bmatrix} 1.5 & 0 \\ 0 & 1.5 \end{bmatrix}}^{L-1}x$$
그렇게 되면 본질적으로 $\hat{y}$은 $1.5^{L-1}x$ 가 된다
여기서 $L$이 매우 큰 깊은 신경망이라면 $\hat{y}$의 값도 매우 커질 것이다 (기하급수적으로)
--> explode
반면에 $w^{[l]} = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix}$ 라고 한다면,
$\hat{y}$은 $0.5^{L-1}x$ 가 되므로, 활성화값이 기하급수적으로 작아진다
따라서 weight의 값들이 1보다 크면, 즉 $w^{[l]} > I$로 identity matrix보다 크면 깊은 신경망에서 활성화값은 explode 할 것이고 1보다 작으면 기하급수적으로 작아질 것이다
이에 gradient들도 기하급수적으로 커지거나 작아질 것이다
Weight Initialization for Deep Networks
위에서 이야기한 문제를 부분적으로 해결할 수 있는 방법
[single neuron example]

$b=0$이라고 치고
$$z = w_{1}x_{1}+w_{2}x_{2}+ \ldots + w_{n}x_{n}$$
$z$가 너무 크거나 작지 않게 하려면 $n$이 클수록 $w_{i}$가 작아져야 한다 ( $z$는 $w_{i}x_{i}$ 이므로)
$n$ : the number of input features
한가지 방법은 $w_{i}$의 variance가 $\frac{1}{n}$이게 하는 것
$$Var(w_{i}) = \frac{1}{n}$$
이를 위해서는, 어떤 레이어의 weight matrix $W^{[l]}$를 세팅할 떄 아래와 같이
$$W^{[l]} = np.random.rand(shape \ldots) \times np.sqrt(\frac{1}{n^{[n-1]}})$$
$n^{[n-1]}$ : layer $l$에 입력되는 feature의 개수
이때 ReLU 함수를 쓰고 있다면($g^{[l]}(z) = ReLU(z)$), $Var(w_{i}) = \frac{2}{n}$ 인 것이 조금 더 낫다
if Gaussian random vairable is multiplied by a square root of $\frac{1}{n}$(or $\frac{2}{n}$), that sets the varinace to be equal to $\frac{1}{n}$(or $\frac{2}{n}$)
만약 input feature 들의 평균이 약 0이고 standard variance가 1이면, $z$는 비슷한 scale이 될 것이다
이것이 vanishing/exploding gradient problem을 해결해주는 것은 아니지만 도움은 된다
because it's trying to set each of the weight matrices $W$ so that it's not too much bigger than 1 and not too much less than 1, so it doens't explode or vanish too quickly
----
만약 tanh 함수를 쓰고 있다면, $\frac{1}{n^{[l-1]}}$가 낫다고 한다 즉
$$W^{[l]} = np.random.rand(shape \ldots) \times \sqrt{\frac{1}{n^{[l-1]}}}$$
--> Xavier initialization
$ \sqrt{\frac{2}{n^{[l-1]+n^{[l]}}}}$ 가 좋다는 논문도 있음
It gives you a default value to use for the variance of the initialization of your weight matrices
이 variance parameter도 튜닝 가능한 하이퍼파라미터임 ($np.random.rand(shape \ldots)$ 뒤에 곱할 것)
우선순위로 따지만 낮긴 함
'인공지능 > DLS' 카테고리의 다른 글
| [2.2.] Optimization Algorithms(1) (0) | 2022.07.11 |
|---|---|
| [2.1.] Setting Up your Optimization Problem(2) (0) | 2022.07.06 |
| [2.1.] Regularizing your Neural Network (0) | 2022.07.03 |
| [2.1.] Setting up your Machine Learning Application (0) | 2022.07.03 |
| 강좌1 정리 노트 (0) | 2022.07.03 |