Convolutions Over Volume
3D volume에 convolution 적용하기
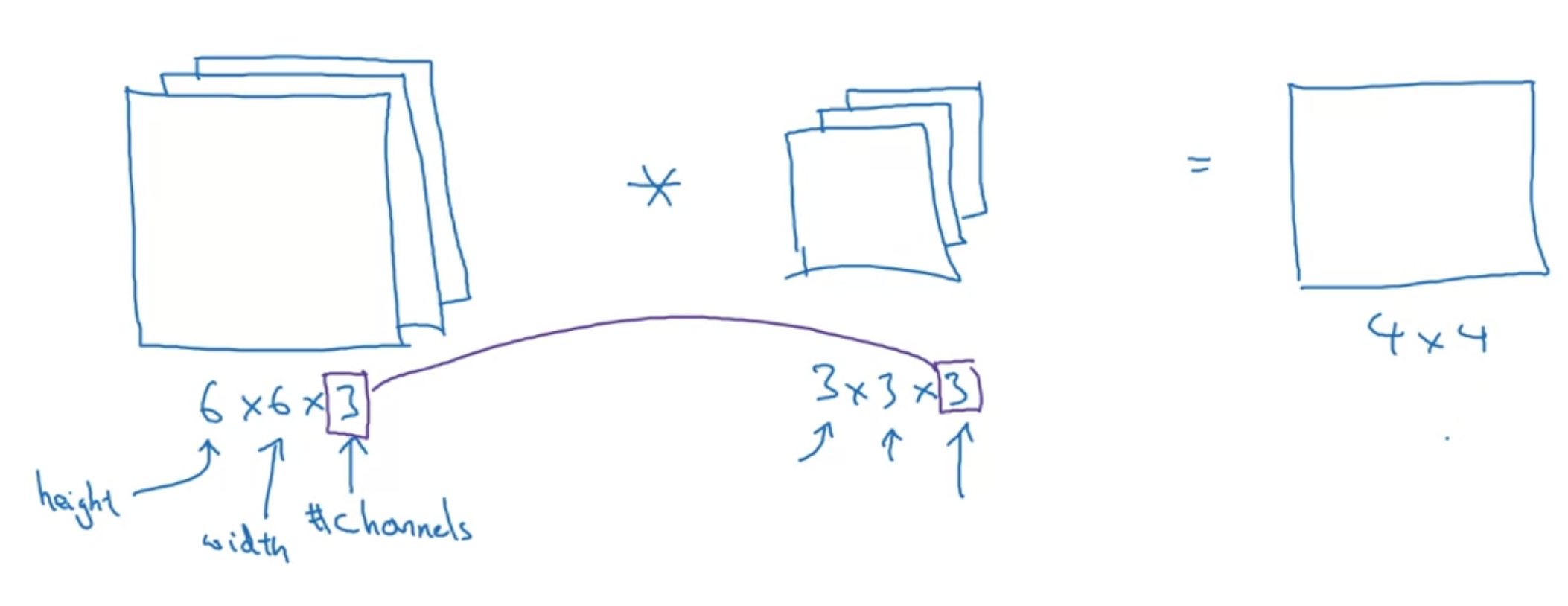
[Convolutions on RGB images]

"height x width x 채널수"
입력 이미지의 채널수와 filter의 채널 수는 일치해야 한다
출력 이미지는 4x4 사이즈가 됨 - 2D output
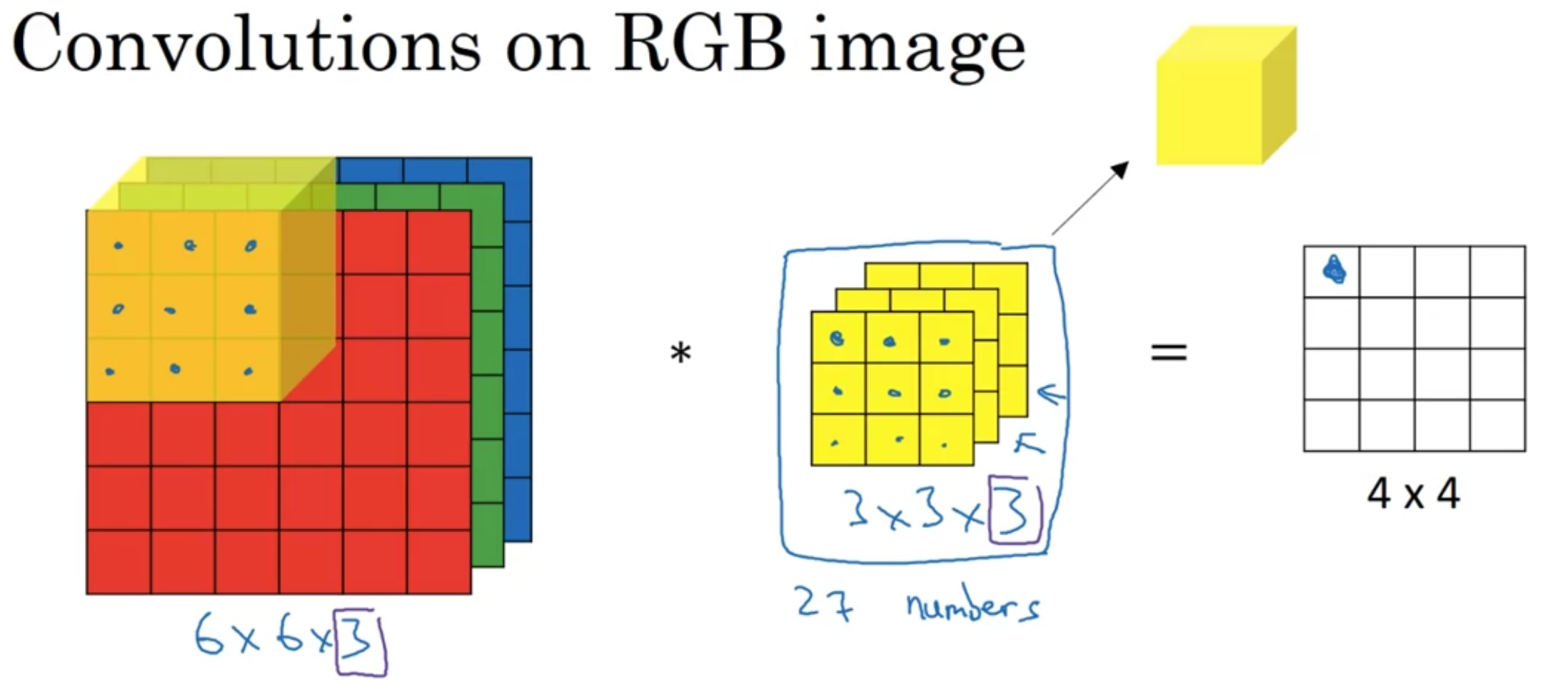
filter들을 각 채널에 포개서 곱하고, 그 값들(27개)을 모두 더함
채널수만큼 포개진 filter를 "R채널의 vertical edge만을 찾게" 만든다면 아래와 같이 구성할 수 있음
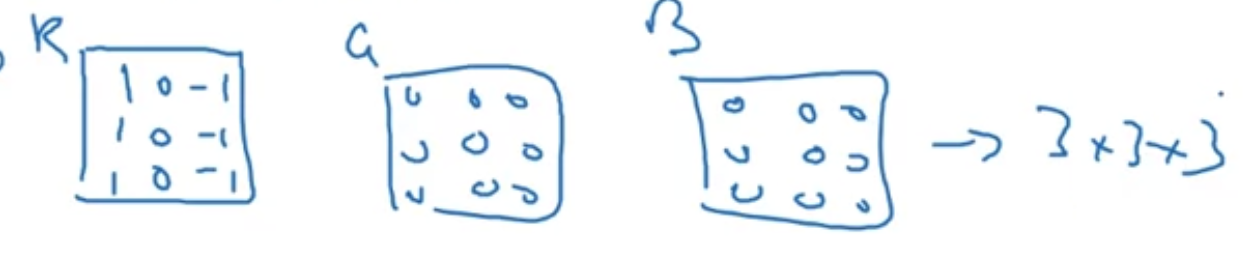
vertical edges in any color? -> RGB 필터 전부 똑같이 채우면 됨
[Multiple filters]
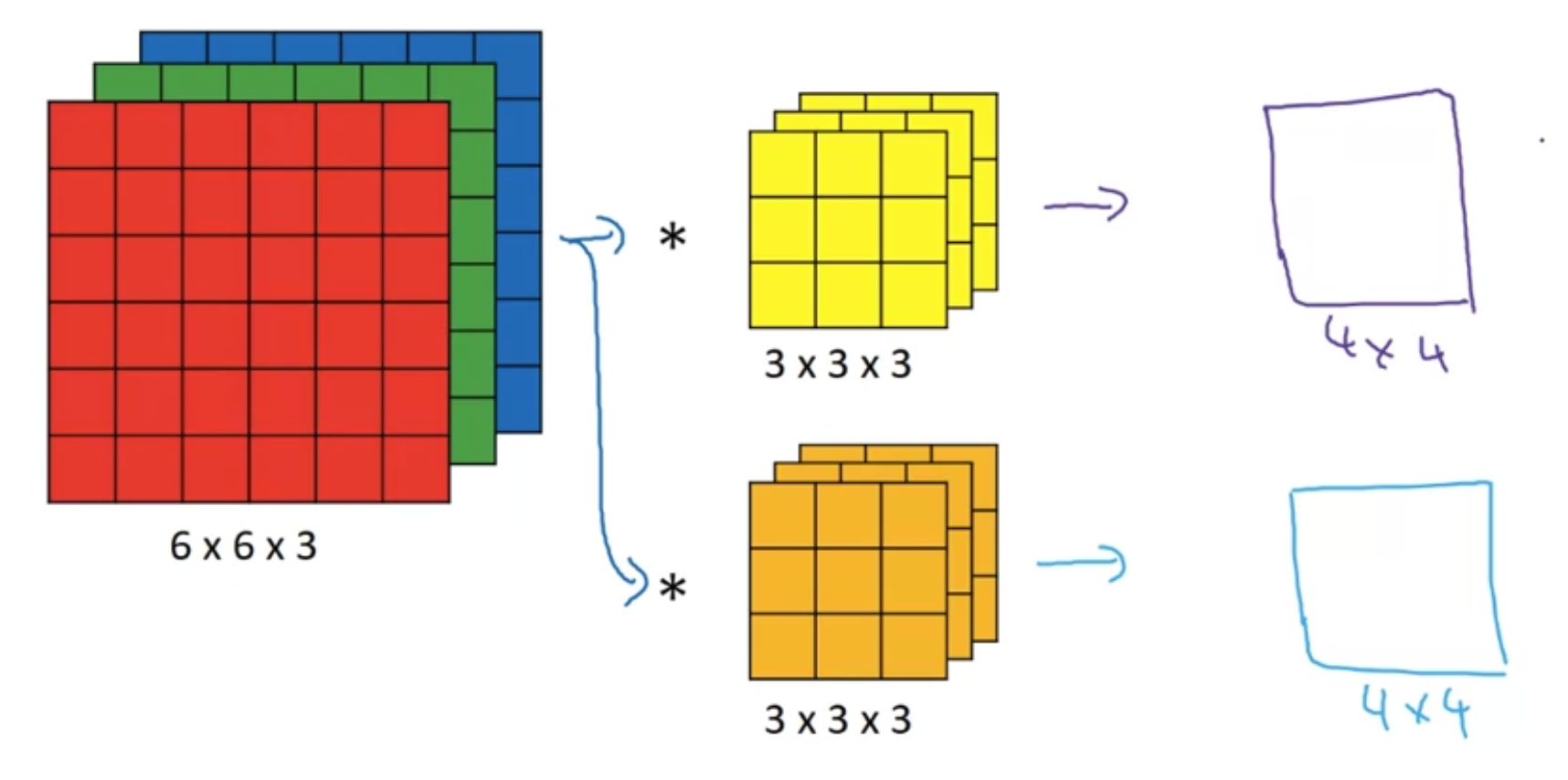
여러 개의 필터를 한번에 적용해보고 싶다면?

필터의 개수만큼 생긴 output 이미지들을 쌓아(stack) 새로운 volume을 생성할 수 있다

두 개의 다른 filter를 적용했으므로 (vertical 하나, horizontal 하나) 두 개의 output 을 쌓을 수 있음--> 4 x 4 x 2
정리하면,
$$n \times n \times n_{c}\ \ \ \ast \ \ \ f \times f \times n_{c}\ \rightarrow\ n-f+1 \times n-f+1 \times n_{c}'$$
$n_{c}$개 채널을 가진 높이 $n$, 폭 $n$의 이미지에
$n_{c}'$ 종류의 높이 $f$, 폭 $f$ filter를 적용하면 (이때 각 filter의 채널수는 입력 이미지와 동일하게 $n_{c}$개)
$n_{c}'$개를 쌓은 $n-f+1$ x $n-f+1$ 사이즈 이미지가 나온다
(output의 채널수 = 사용한 filter의 개수)
- 이때 stride는 $1$, padding은 $0$으로 가정
*channel 대신에 "depth"이라는 말 쓰기도 함
One Layer of a Convolutional Network
위 과정을 convolutional layer로 표현하기

4x4 크기의 각 output 이미지에 (1) 실수 bias를 더한 후 (2) ReLU에 통과시킨다(non-linearity)
- 실수 bias를 더할 때는 파이썬의 broadcasting 사용
그리고 두 output 이미지를 쌓아 4x4x2 의 볼륨으로 만든다
--> 여기까지가 one layer of a convolutional neural network
non-convolution한 forward prop을 생각해보면
$$z^{[1]} = w^{[1]}a^{[0]} + b^{[1]}$$
$$a^{[1]} = g(z^{[1]})$$
그대로 적용한다면
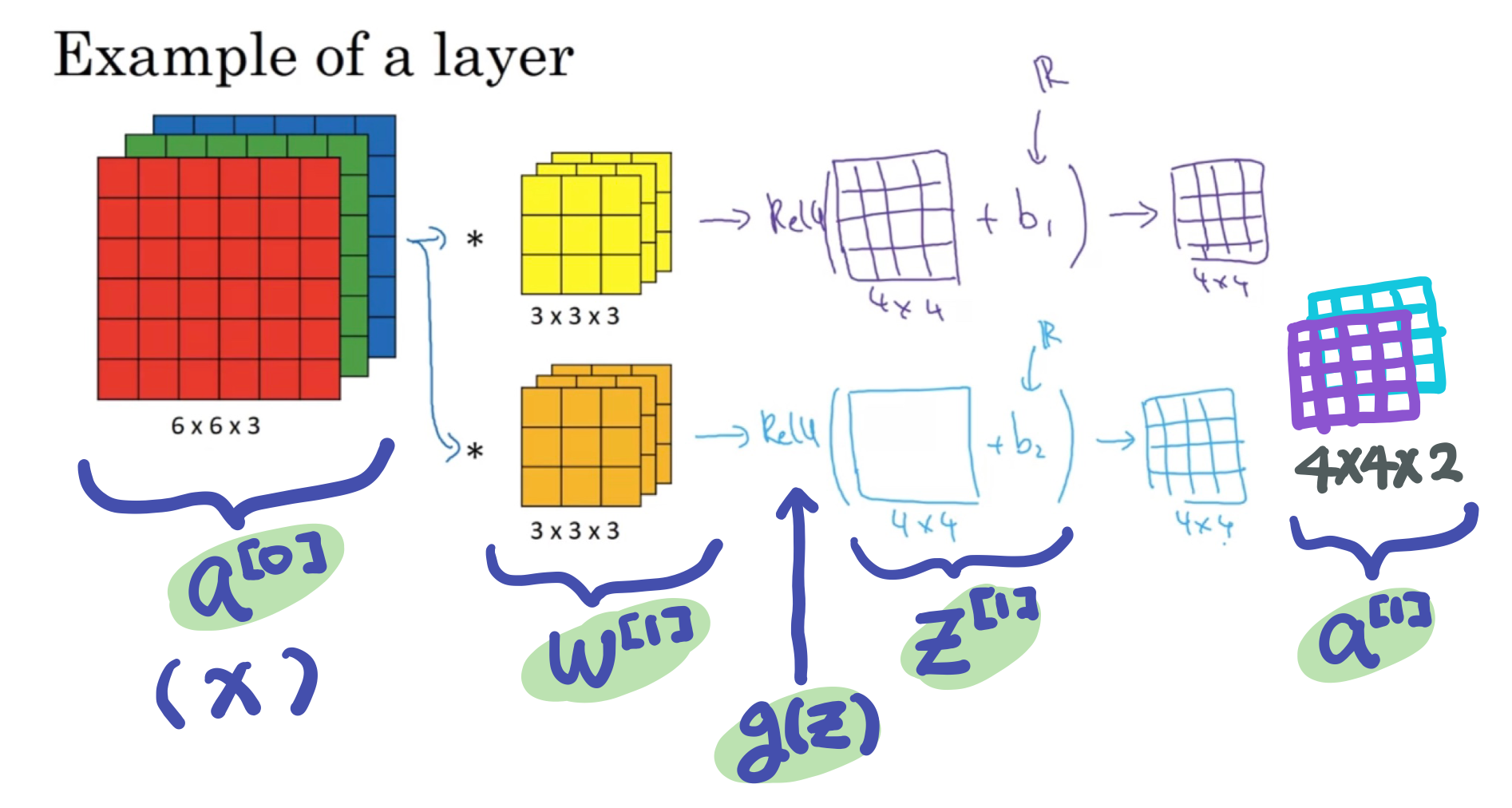
즉 convolution이 linear한 연산

필터당 파라미터 27개 (3*3*3), bias 1개 --> 28개
10개 필터가 있으므로 --> 280개
conv net의 장점: 입력 이미지가 얼마나 커지든 이 parameter의 개수는 고정 --> overfitting의 위험이 낮음
[notation]
If layer $l$ is a convolution layer:
- $f^{[l]}$ : filter 사이즈
- $p^{[l]}$ : padding 사이즈
- $s^{[l]}$ : stride 사이즈
- $n^{[l]}_{c}$ : filter의 개수
- 입력 이미지 : $n^{[l-1]}_{H} \times n^{[l-1]}_{W} \times n^{[l-1]}_{c}$
- 출력 이미지 : $n^{[l]}_{H} \times n^{[l]}_{W} \times n^{[l]}_{c}$
$$n^{[l]}_{H} = \lfloor \frac{n^{[l-1]}_{H} + 2p^{[l]} - f^{[l]}}{s^{[l]}} \rfloor$$
$$n^{[l]}_{W} = \lfloor \frac{n^{[l-1]}_{W} + 2p^{[l]} - f^{[l]}}{s^{[l]}} \rfloor$$
- 각 필터 : $f^{[l]} \times f^{[l]} \times n^{[l-1]}_{c}$
- activations a^{[l]} : $n^{[l]}_{H} \times n^{[l]}_{W} \times n^{[l]}_{c}$
- weights : $ f^{[l]} \times f^{[l]} \times n^{[l-1]}_{c} \times n^{[l]}_{c}$
- bias : $n^{[l]}_{c}$ - $(1, 1, 1, n^{[l]}_{c})$
$$A^{[l]} = m \times n^{[l]}_{H} \times n^{[l]}_{W} \times n^{[l]}_{c}$$
* $m$ : batch back prop
*$n^{[l]}_{c}$를 먼저 쓰기도 함
Simple Convolutional Network Example

<입력 이미지 $x$>
39 x 39 x 3
<첫번째 conv 레이어>
필터크기 3, stride 1, padding 0, 필터개수 10
활성화함수 지나 출력값 --> 37 x 37 x 10
<두번째 conv 레이어>
필터크기 5, stride 2, padding 0, 필터개수 20
활성화함수 지나 출력값 --> 17 x 17 x 20
<마지막 conv 레이어>
필터크기 5, stride 2, padding 0, 필터개수 40
활성화함수 지나 출력값 --> 7 x 7 x 40
<마지막 레이어>
7 x 7 x 40, 즉 1,960개의 값을 길쭉한 벡터로 unroll
이 값들을 logistic/softmax 에 입력하여 $\hat{y}$를 출력한다
- 이미지의 사이즈는 점점 작아지는데, 채널의 수는 점점 늘어난다
[types of layer in a convolutional network]
- convolution (conv)
- pooling (POOL)
- fully connected (FC)
'인공지능 > DLS' 카테고리의 다른 글
| [4.2.] Case Studies(1) (0) | 2022.07.24 |
|---|---|
| [4.1.] Convolutional Neural Networks(3) (0) | 2022.07.24 |
| [4.1.] Convolutional Neural Networks(1) (0) | 2022.07.23 |
| [3.2.] End-to-end Deep Learning (0) | 2022.07.20 |
| [3.2.] Learning from Multiple Tasks (0) | 2022.07.20 |