
[문제]


[내 코드]
N = int(input()) # 도시의 개수
M = int(input()) # 버스의 개수
# 버스의 출발도시, 도착도시, 비용
graph = {}
for n in range(N):
graph[n+1] = {}
for _ in range(M):
a, d, c = map(int, input().split())
graph[a][d] = c
start, end = map(int, input().split())
def bellman_ford(graph, start):
dist = {}
for node in range(1, N+1):
dist[node] = float('inf')
dist[start] = 0
# V-1 번 반복
for i in range(N-1):
for node in graph:
for nextNode in graph[node]:
if dist[nextNode] > dist[node]+graph[node][nextNode]:
dist[nextNode] = dist[node]+graph[node][nextNode]
return dist
print(bellman_ford(graph, start)[end])벨만포드 알고리즘에 대해 공부를 한 후 적용을 했으나, 시간초과
음수 간선이 있을 때 벨만포드를 쓰는 거로 배웠으니.. 그렇다면 다익스트라로?
import heapq
INF = int(1e9) #무한을 의미하는 값으로 10억을 설정.
#노드의 개수, 간선의 개수를 입력받기
n = int(input())
m = int(input())
#각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
#최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)
#모든 간선 정보를 입력받기
for _ in range(m):
a, b, c = map(int, input().split())
#a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].append((b, c))
start, end = map(int, input().split())
def dijkstra(start):
q = []
#시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
heapq.heappush(q, (0, start))
distance[start] = 0
while q: #큐가 비어있지 않다면
#가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
dist, now = heapq.heappop(q)
# 현재 노드가 이미 처리된 적이 있는 노드라면 무시
if distance[now] < dist:
continue
# 현재 노드와 연결된 다른 인접한 노드들을 확인
for i in graph[now]:
cost = dist + i[1]
#현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[i[0]]:
distance[i[0]] = cost
heapq.heappush(q, (cost, i[0]))
dijkstra(start)
print(distance[end])를 했으나 시간 초과... 답을 봐보기로 했다
[개선안]
import heapq
n = int(input())
m = int(input())
graph = [[] for _ in range(n + 1)]
visited = [float('inf')] * (n + 1)
for _ in range(m):
a, b, c = map(int, input().split())
graph[a].append((c, b))
start, end = map(int, input().split())
def dijkstra(x):
pq = []
heapq.heappush(pq, (0, x))
visited[x] = 0
while pq:
d, x = heapq.heappop(pq)
if visited[x] < d:
continue
for nw, nx in graph[x]:
nd = d + nw
if visited[nx] > nd:
heapq.heappush(pq, (nd, nx))
visited[nx] = nd
dijkstra(start)
print(visited[end])
함수의 내용은 똑같은데.. 뭐가 다른가 해서 봤더니
- input = sys.stdin.readline 으로 입력값을 받았다
- float('inf') 대신에 from sys import maxsize 해서 [maxsize]로 무한대를 세팅해주었다
ㅠㅠ 이것도 차이가 크구나
[이해를 위한 노력]
문제에서 제시된 예제대로 입력하면 graph 는 아래와 같이 만들어진다
[[], [(2, 2), (3, 3), (4, 1), (5, 10)], [(4, 2)], [(4, 1), (5, 1)], [(5, 3)], []]
파이썬의 heap 모듈 heapq 를 사용한다 (자료구조 heap에 대한 글은 여기에 작성했다)
heapq에 튜플 형태로 heappush 하면 첫번째 요소를 기준으로 큐가 정리된다
import heapq
q = []
heapq.heappush(q, (2, 1))
heapq.heappush(q, (4, 2))
heapq.heappush(q, (1, 3))
heapq.heappush(q, (3, 4))
print(q)
# [(1, 3), (3, 4), (2, 1), (4, 2)](위와 같이 출력되는 이유는 아래 그림 참고.. 아직 익숙하지 않아서 그림 그려가며 이해해야 한다;;)
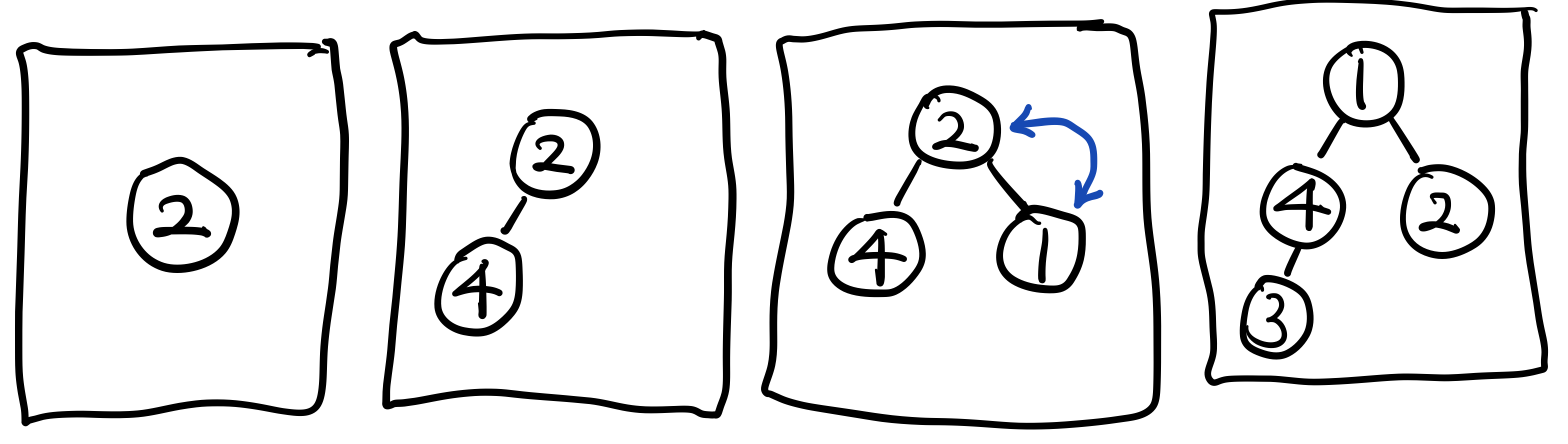
처음 시작노드로 가는 경로는 당연히 0이므로, 큐와 distance에 0을 넣어준다 (x 는 시작 노드)
heapq.heappush(pq, (0, x))
visited[x] = 0
while문 시작
거리가 가장 짧은 것을 꺼낸다 - 튜플 형식으로 넣었으므로 튜플 형식으로 나옴. 따라서 d는 거리고 x는 노드다
*heappop 하면 가장 작은 요소부터 꺼내며 제거한다
d, x = heapq.heappop(pq)
- 기존 노드의 거리 (visted[nx])가 큐에서 꺼낸 거리(d)보다 짧으면 pass 한다
- 그렇지 않을 때, graph 에서 그 노드와 인접한 노드까지의 거리를 꺼낸다 (nw는 경로값, nx는 노드)
- 큐에서 꺼낸 거리(d)에 노드까지의 거리(nw)를 더한다(nd)
- 그 값이 기존 노드의 거리(visted[nx])보다 짧으면, 큐와 거리리스트(visited)를 업데이트 해준다
# 시작점에서 x노드까지의 기록된 (기존) 거리
# 큐에서 꺼낸 거리
if visited[x] < d:
continue
# x노드와 인접한 노드들(nx)까지의 거리(nw)
for nw, nx in graph[x]:
nd = d + nw
# 시작점에서, x와 인접한 노드(nx)까지의 거리
# 큐에서 꺼낸 거리 + x와 인접한 노드까지의 거리
if visited[nx] > nd:
heapq.heappush(pq, (nd, nx))
visited[nx] = nd
계속 헷갈려서 🤣🙃 while문 돌 때마다 큐와 거리리스트를 print 해보았다
참고로 예제를 그림으로 그리면 아래와 같음

첫 iter 때는 출발점 빼고는 무한대이다
큐: [(0, 1)]
visited [inf, 0, inf, inf, inf, inf]
그 다음, 출발점과 인접한 것들까지의 거리가 큐에 담기고 거리리스트도 업데이트 되었다
큐: [(1, 4), (3, 3), (2, 2), (10, 5)]
visited [inf, 0, 2, 3, 1, 10]
큐에서 거리가 가장 짧은 것부터 꺼내서 본다 - 정점4에서 정점5로 가는 값이 1
정점4까지 갔던 거리와 정점4에서 정점5로 가는 값을 더한 다음에 (4) 원래 정점5로 갔던 값(10)이랑 비교해서, 전자가 더 작으니 visited 에서 교체해준다
큐: [(2, 2), (3, 3), (10, 5), (4, 5)]
visited [inf, 0, 2, 3, 1, 4]
나머지 정점들은, 정점1과 인접한 길로 바로 가는 게 이미 최단경로여서 더이상 업데이트 되지 않는다
큐: [(3, 3), (4, 5), (10, 5)]
visited [inf, 0, 2, 3, 1, 4]
큐: [(4, 5), (10, 5)]
visited [inf, 0, 2, 3, 1, 4]
큐: [(10, 5)]
visited [inf, 0, 2, 3, 1, 4]
우아... 진짜 힘들었다.
(지금도 제대로 이해한 건지 잘 모르겠으니 여러번 반복해서 봐야 할 듯)
'컴퓨터 > 코딩테스트' 카테고리의 다른 글
| [백준/약점체크] 16916번: 부분문자열 (2) | 2022.10.07 |
|---|---|
| [백준/약점체크] 1197번: 최소 스패닝 트리 (1) | 2022.10.05 |
| [백준/약점체크] 1806번: 부분합 (1) | 2022.09.25 |
| [백준/약점체크] 1700번: 멀티탭 스케줄링 (2) | 2022.09.24 |
| [백준/약점체크] 1062번: 가르침 (1) | 2022.09.24 |