
그래프를 탐색하는 알고리즘에는 DFS(Depth-First Search, 깊이 우선 탐색)과 BFS(Breadth-First Search, 너비 우선 탐색)이 있다.
오늘은 DFS 알고리즘에 대해 알아보자.
그래프를 탐색한다는 것 = 하나의 정점에서 시작하여 그래프의 모든 정점들을 방문하는 것
알아야 할 용어 : 루트 노드 (뿌리), 형제 노드 (같은 레벨에 놓은 노드들), 자식 노드 (어떤 노드 아래에 속한 노드)

DFS(깊이 우선 탐색)
"한 놈만 팬다"
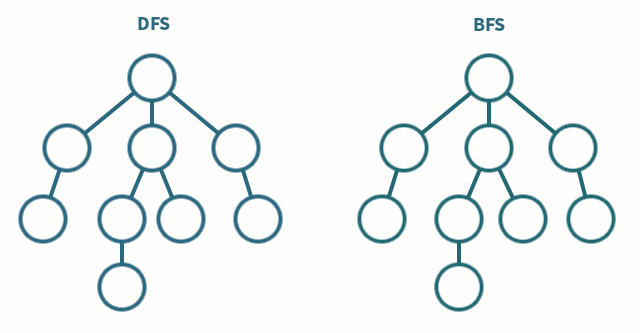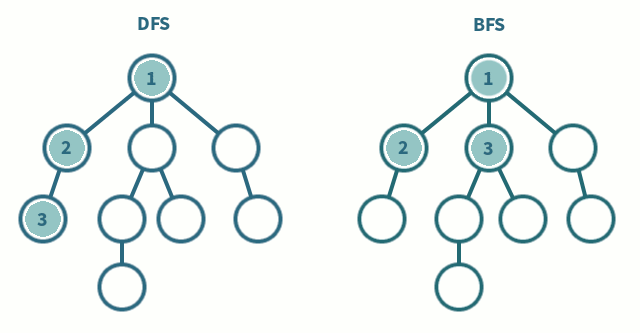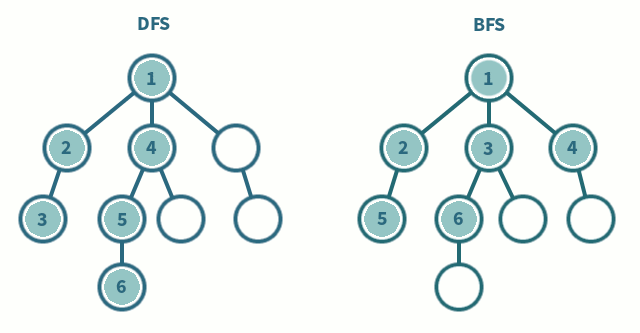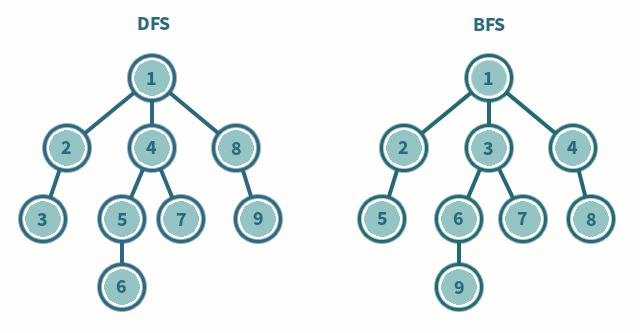
- 임의의 노드에서 시작해 자식 노드를 타고 제일 깊숙히 내려간다. 다시 돌아와 다른 형제 노드의 자식 노드를 타고 제일 깊숙히 내려간다.
- DFS가 언제 필요할까? 모든 노드를 방문하고자 할 때 (모든 경우의 수를 구할 때 쓰기에 좋겠다!)
- 코드는 DFS가 BFS보다 간단하지만, 검색 속도는 DFS가 BFS보다 느리다.

방문 순서
A → B → E → I → J → C → F → D → G → H → K
스택을 활용한 구현
DFS는 스택(stack)을 활용할 수 있다! 스택은 후입선출의 자료구조로, 나중에 들어온 데이터가 먼저 나가게 된다.
그러니까 스택에 노드들을 차곡차곡 넣을 건데(push), 꺼낼 때는 방금 넣은 노드를 먼저 꺼내 출력한다(pop).
위의 방문 순서(A → B → E → I → J → C → F → D → G → H → K)대로 출력하게끔 스택을 활용해보자.
처음 임의의 노드(루트 노드)를 스택에 push한 다음,
단계별로 (1) pop 하면서 (2) pop된 노드의 자식 노드들을 push 한다. 단지 이것의 반복이다.


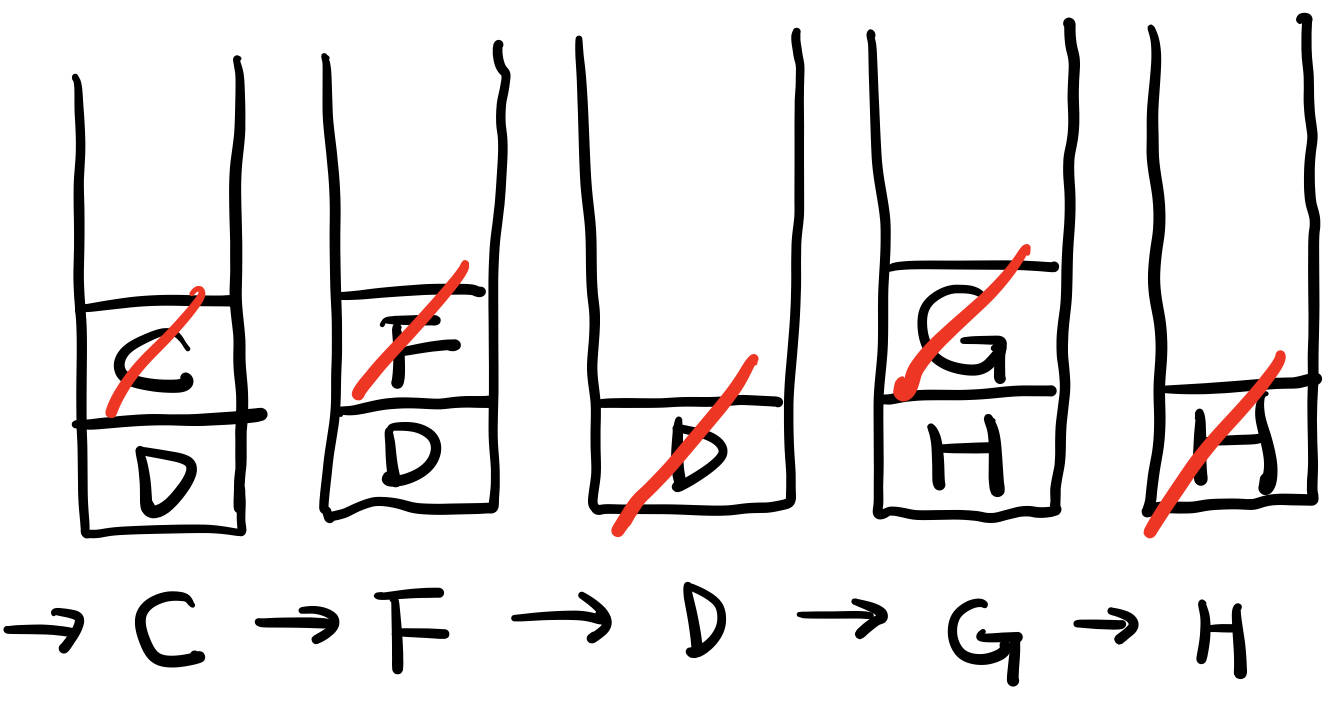
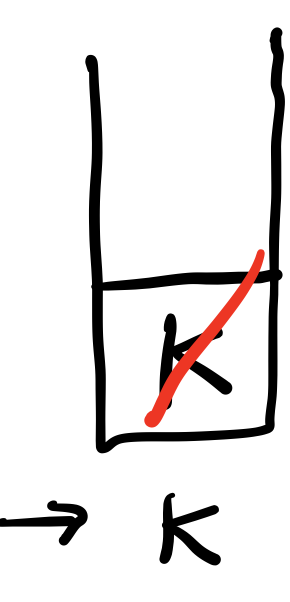
빨간색 대각선은 pop(제거 및 출력)을 의미한다. 단계별로 출력된 것은 스택 아래 써놨다.
예를 들어,
[1] 처음 A를 스택을 push 했다. 다음 A를 pop하면서 A의 자식 노드들인 B, C, D 를 push 한다.
[2] 그 다음 B를 pop하면서 B의 자식 노드인 E를 push 한다.
...
[4] I를 pop하는데, I는 자식 노드가 없으므로 아무것도 push되지 않는다.
[5] J를 pop하는데, J는 자식 노드가 없으므로 아무것도 push되지 않는다.
...
*개인적으로 헷갈렸던 것
'A'의 자식노드들인 'B, C, D' 를 push하고 나서, 그 다음 단계에서는 선입후출 방식에 따라 가장 마지막의 'D'를 먼저 pop해야 하지 않나..?
하지만 그림 상으로는 'B, C, D'를 세로로 쌓아서 사실상 'D, C, B' 순서로 들어간 게 되었다.
일단 그림으로 이해하고 코드를 통해 좀더 확실하게 봐보자!!!
파이썬 코드
먼저 딕셔너리와 리스트를 활용해서 그래프를 정의한다.
'인접리스트' 방식을 사용했다. (그래프 자료구조에 대해 글 작성 예정)

graph = {
'A': ['B', 'C', 'D'],
'B': ['A', 'E'],
'C': ['A', 'F'],
'D': ['A', 'G', 'H'],
'E': ['B', 'I', 'J'],
'F': ['C'],
'G': ['D'],
'H': ['D', 'K'],
'I': ['E'],
'J': ['E'],
'K': ['H']
}
그 다음 DFS 탐색 함수를 정의한다. 스택은 list로 구현했고, 출력 결과는 visit에 담긴다.
def dfs(graph, start_node):
visit = list()
stack = [start_node]
while stack:
node = stack.pop()
if node not in visit:
visit.append(node)
stack.extend(reversed(graph[node]))
return visit
print(dfs(graph, 'A'))
# ['A', 'B', 'E', 'I', 'J', 'C', 'F', 'D', 'G', 'H', 'K']- 먼저 stack에 시작 정점을 넣어 초기화한다.
- stack에 요소가 있는 동안 반복할 내용:
- stack에서 node를 pop한다
- node가 visit 명단에 없으면 visit 명단에 넣는다
- 그 노드의 인접 노드들을 stack에 push한다
- 위에서는 자식 노드만을 push한다고 설명했는데, 코드상으로는 부모노드까지 인접한 노드는 모두 push한다
- 부모노드는 이미 visited 리스트에 들어있기 마련이므로, 'if node not in visit'에 해당하지 않아 pass될 것이다
- extend : 인자로 받은 리스트를 풀어서 그 요소들을 append 한다
- reversed : 위에서 내가 헷갈려 했던 부분이었는데, 요소를 있는 그대로 append하지 않고 순서를 거꾸로 append 했다
# ['A']
# ['D', 'C', 'B']
# ['D', 'C', 'E', 'A'] <- 부모노드 'A'가 이미 visited에 있으므로 pass
# ['D', 'C', 'E']
# ['D', 'C', 'J', 'I', 'B'] <- 부모노드 'B'가 이미 visited에 있으므로 pass
# ['D', 'C', 'J', 'I']
# ['D', 'C', 'J', 'E'] <- 부모노드 'E'가 이미 visited에 있으므로 pass
# ['D', 'C', 'J']
# ['D', 'C', 'E'] <- 부모노드 'E'가 이미 visited에 있으므로 pass
# ['D', 'C']
# ['D', 'F', 'A'] <- 부모노드 'A'가 이미 visited에 있으므로 pass
# ['D', 'F']
# ['D', 'C'] <- 부모노드 'C'가 이미 visited에 있으므로 pass
# ['D']
# ['H', 'G', 'A'] <- 부모노드 'A'가 이미 visited에 있으므로 pass
# ['H', 'G']
# ['H', 'D'] <- 부모노드 'D'가 이미 visited에 있으므로 pass
# ['H']
# ['K', 'D'] <- 부모노드 'D'가 이미 visited에 있으므로 pass
# ['K']
# ['H'] <- 부모노드 'H'가 이미 visited에 있으므로 pass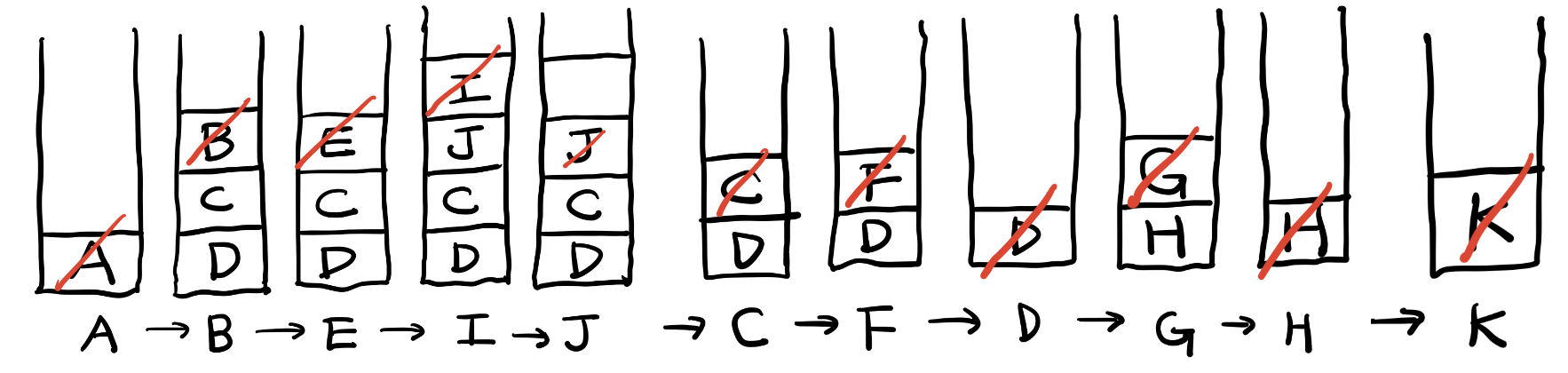
while문마다 stack을 찍어 확인해보았다. 이미 visited에 올라간 부모 노드를 pop해서 pass 하는 경우를 제외하고 보면 그림과 동일하다.
재귀를 활용한 구현
제일 먼저 시작된 함수를 가장 마지막에 처리한다는 점에서 재귀는 스택 구조(메모리)를 활용한다.
잠에 들어 꿈을 꾸었는데,
꿈 속에서 잠에 들어 꿈을 꾸었는데,
꿈 속에서 잠에 들어 꿈을 꾸었는데,
꿈 속에서 잠에 들어 꿈을 꾸었는데
그 꿈에서 깨어났고,
그 꿈에서 깨어났고,
그 꿈에서 깨어났고,
꿈에서 깨어났다.
제일 먼저 시작된 꿈은 마지막에 깨어날 수 있다. 재귀함수는 이러한 원리다.
바로 코드로 살펴보자.
visited = []
def dfs_recursive(graph, start):
# 이미 방문한 노드라면 탐색 종료
if start in visited:
return
# 방문 표시
visited.append(start)
print(start, end=' ')
# 인접 정점들에 대해 재귀 호출
for now in graph[start]:
dfs_recursive(graph, now)
dfs_recursive(graph, 'A')
# A B E I J C F D G H K
dfs_recursive(graph, 'A') 로 처음 함수를 호출했다
- 'A'가 visited에 없으므로 'A'를 visited에 넣고, 출력한다
- 'A'와 인접한 노드들 'B, C, D'로 for문 실시
- 'B'가 visited에 없으므로 'B'를 visited에 넣고, 출력한다
- 'B'와 인접한 노드들로 for문 실시
- dfs_recursive(graph, 'A') : 'A'가 visited에 있으므로 해당 재귀 함수 종료(return)
- dfs_recursive(graph, 'E') :
- 'E'가 visited에 없으므로 'B'를 visited에 넣고, 출력한다
- 'E'와 인접한 노드들로 for문 실시
...
- 'C'가 visited에 없으므로 'C'를 visited에 넣고, 출력한다
- 'C'와 인접한 노드들로 for문 실시
- dfs_recursive(graph, 'A') : 'A'가 visited에 있으므로 해당 재귀 함수 종료(return)
- dfs_recursive(graph, 'F') :
- 'F'가 visited에 없으므로 'B'를 visited에 넣고, 출력한다
- 'F'와 인접한 노드들로 for문 실시
...
시간 복잡도
V는 정점의 개수, E는 간선의 개수다.
DFS를 정점의 개수만큼 부르게 되는데, 인접리스트로 구현한 경우 DFS 하나당 인접 정점들을 모두 탐색하므로 시간 복잡도는 $O(V+E)$ 이다.
반면, 인접행렬로 구현한 경우 시간 복잡도는 $O(V^{2})$ 이다.
예제
백준 14888번 연산자 끼워넣기에서 DFS를 활용했다. 연산자들의 경우의 수를 DFS식으로 탐색해나가며 연산 결과의 최댓값과 최솟값을 구했다.
https://woo-niverse.tistory.com/212
[백준/약점체크] 14888번: 연산자 끼워넣기
이 문제 재밌었다.. [문제] [내 코드] from itertools import permutations import operator cnt = int(input()) - 1 arr = list(map(str, input().split())) ops_cnt = [] for i, j in zip(input().split(), ['+..
woo-niverse.tistory.com
'컴퓨터 > 알고리즘&자료구조' 카테고리의 다른 글
| 정렬 알고리즘 : 위상 정렬 (Topological Sorting) (1) | 2022.10.11 |
|---|---|
| 그래프 탐색 : BFS(너비 우선 탐색) (1) | 2022.10.07 |
| 문자열 검색 : LPS와 KMP 알고리즘 (2) | 2022.10.06 |
| 최소 신장 트리 구하기 : 프림(Prim's) 알고리즘 (0) | 2022.10.05 |
| 최소 신장 트리 구하기 : 크루스칼(Kruskal) 알고리즘 (0) | 2022.10.05 |