
지난 글에서 DFS(깊이 우선 탐색)에 대해 알아보았다.
오늘은 BFS(너비 우선 탐색)에 대해 알아보자.
BFS(너비 우선 탐색)
- 임의의 노드에서 시작해 인접 노드를 먼저 탐색한다.
- 두 노드 사이의 최단 경로를 알고 싶을 때 실시할 수 있다. (DFS의 경우 모든 그래프를 살펴봐야 할 수 있음)

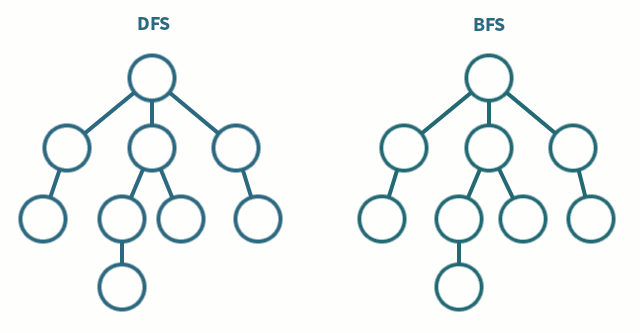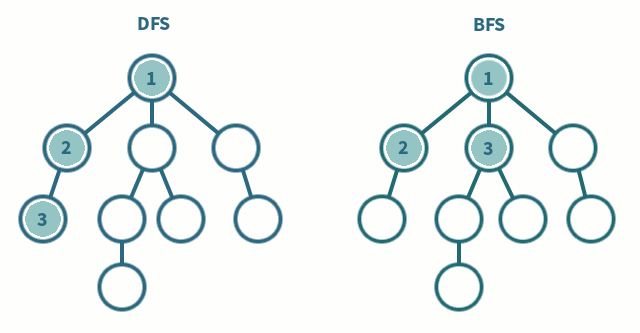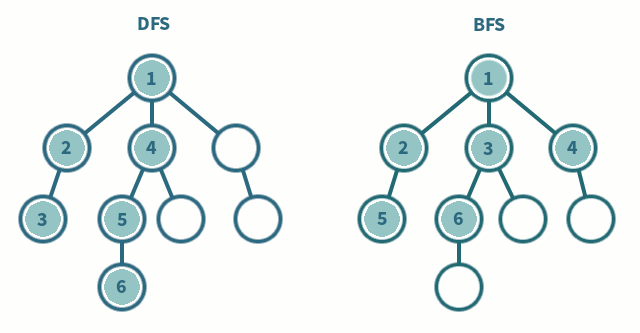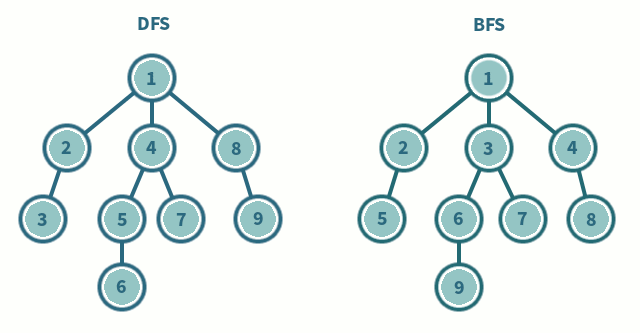
방문 순서
A → B → C → D → E → F → G → H → I → J → K
큐를 활용한 구현
BFS는 큐를 활용할 수 있다. 큐는 선입선출의 자료구조로, 먼저 들어온 데이터가 먼저 나가게 된다.
BFS에서는 지금 시점에서 방문할 수 있는 노드들을 큐에 넣게 된다.



A를 출력하면서, A의 인접 노드들을 쌓는다. 그 다음은 먼저 들어갔던 노드가 출력된다. 반복.
먼저 인접리스트 형식으로 그래프를 정의한다.
graph = {
'A': ['B', 'C', 'D'],
'B': ['A', 'E'],
'C': ['A', 'F'],
'D': ['A', 'G', 'H'],
'E': ['B', 'I', 'J'],
'F': ['C'],
'G': ['D'],
'H': ['D', 'K'],
'I': ['E'],
'J': ['E'],
'K': ['H']
}
그 다음 Queue 모듈을 불러와 활용
from queue import Queue
def bfs(graph, start_node):
visit = list()
q = Queue()
q.put(start_node)
while q.qsize() > 0:
node = q.get()
if node not in visit:
visit.append(node)
for nextNode in graph[node]:
q.put(nextNode)
return visit
print(bfs(graph, 'A'))
# ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K']
collections의 deque 를 사용할 수도 있다. deque는 양방향에서 데이터를 처리할 수 있는 큐 자료구조다.
from collections import deque
def bfs_deque(graph, start_node):
visited = []
q = deque([start_node])
while q:
node = q.pop()
if node not in visited:
visited.append(node)
q.extendleft(graph[node])
return visited
print(bfs_deque(graph, 'A'))
# ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K']
deque의 extendleft 는 list의 extend와 같이 요소를 펼쳐 거꾸로(!) 큐에 추가해준다. 이때 left라고 써 있으니 왼쪽에 추가되는 것이다.
아래 코드를 참고하자.
q = deque([1, 2, 3])
q.extendleft([4, 5])
print(q)
# deque([5, 4, 1, 2, 3])
시간 복잡도
언제 BFS를 쓰고, 언제 DFS를 써야 할까?
- 그래프의 정점들을 모두 방문하는 게 중요할 때는 BFS, DFS 중 어느 것을 써도 상관 없다.
- 경로마다 특징이 저장해야 할 때는 DFS 를 쓴다.
- 최단 거리를 찾아야 할 때는 BFS 를 쓴다.
- 그래프의 크기가 매우 크다면 DFS를, 시작 정점으로부터 목표 정점이 멀지 않으면 BFS 를 고려할 수 있다.
예제
(추가 예정)
'컴퓨터 > 알고리즘&자료구조' 카테고리의 다른 글
| 정렬 알고리즘 : 위상 정렬 (Topological Sorting) (1) | 2022.10.11 |
|---|---|
| 그래프 탐색 : DFS(깊이 우선 탐색) (4) | 2022.10.07 |
| 문자열 검색 : LPS와 KMP 알고리즘 (2) | 2022.10.06 |
| 최소 신장 트리 구하기 : 프림(Prim's) 알고리즘 (0) | 2022.10.05 |
| 최소 신장 트리 구하기 : 크루스칼(Kruskal) 알고리즘 (0) | 2022.10.05 |