텐서플로우에서 파이토치로 환승(!)하기 위해 기본적인 내용부터 공부를 하고 있다.
아래의 이전 글들을 참고할 수 있다.
텐서플로우(TensorFlow)에서 파이토치(PyTorch)로 환승하기
이번 글에서는 파이토치의 autograd, 즉 자동 미분에 대해서 알아보려고 한다.
기본적으로 파이토치에서 제공하는 이 도큐먼트를 기반으로 한다.
자동 미분
먼저 개념적으로 살펴보자.
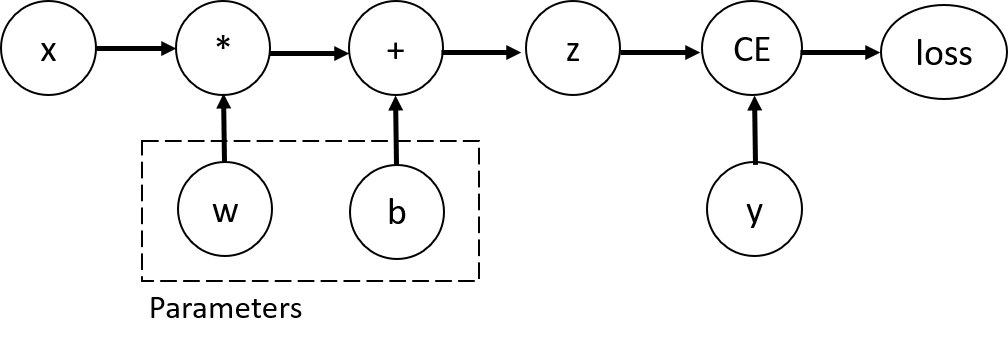
연산이 수행되면서 데이터가 발생한다. 이러한 모든 연산을 저장하는 그래프가 있고, autograd가 이 그래프를 담당한다.
이때 그래프는 유향 비순환 그래프(일명 DAG) 형태를 띠며, 잎(leaves)은 입력텐서 그리고 뿌리(roots)는 출력텐서다.
그래프의 뿌리부터 시작해 잎을 향해 추적하면서, 체인룰을 활용해 그래디언트를 자동 연산할 수 있다.

내부적으로는 어떤 식으로 연산이 이루어지는 걸까?
먼저 위에서 이야기한 그래프는 Function 객체의 그래프로 표현된다.
순전파의 경우, autograd는 주어진 연산을 수행하는 동시에 그래프 하나를 생성한다. 이 그래프는 그래디언트를 연산하는 함수를 나타낸다.
torch.Tensor의 .grad_fn 속성이 이 그래프의 진입점(entry point)가 된다.
중요한 것은 iteration마다 그래프가 처음부터 새로 생성된다는 점이다.
예제
위 내용을 코드를 통해 확인해보자면...
import torch
x = torch.ones(2, 2, requires_grad = True) # (2,2) 모양의 텐서 객체 생성출력 결과: tensor([[1., 1.], [1., 1.]], requires_grad=True)
텐서 객체를 생성하고, 아주 간단한 순전파 연산을 정의해보았다.
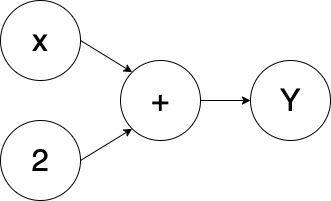
y = x + 2
print(y)출력 결과: tensor([[3., 3.], [3., 3.]], grad_fn=<AddBackward0>)
연산을 수행한 결과, 출력텐서의 grad_fn 속성에 역전파를 위한 정보가 부여되어 있는 것을 확인할 수 있다.
이 상태에서 역전파를 수행하면 에러가 발생하는데
y.backward()출력 결과: RuntimeError: grad can be implicitly created only for scalar outputs
이는 출력텐서인 y가 스칼라가 아닌 벡터이기 때문에 발생하는 것이다. 방법은 두 가지다.
첫째, y를 스칼라로 표현한다. 그렇게 하기 위해 연산을 아래와 같이 수정하고, 역전파 연산을 수행했다.
y = (x + 2).sum() # 출력 결과: tensor(12., grad_fn=<SumBackward0>)
y.backward()
print(x.grad)출력 결과: tensor([[1., 1.], [1., 1.]])
둘째, backward() 함수에 x를 인자로 넣어준다.
y = x + 2 # 출력 결과: tensor([[3., 3.], [3., 3.]], grad_fn=<AddBackward0>)
y.backward(x)
print(x.grad)출력 결과: tensor([[1., 1.], [1., 1.]])
이렇게 아주 간단한 연산 예제를 통해 $\frac{dy}{dx}$ 로 표현되는 그래디언트를 구해보았다.
위의 설명을 반복하자면,
주어진 순전파 연산을 수행하면서 역전파 연산을 위한 그래프 정보가 함께 저장되며, 이는 print 하여 grad_fn 으로 확인할 수 있다.
y = x + 2 # add
z = y * y # mul
w = z * 7 # mul
print(x)
print(y)
print(z)
print(w)
Saved tensors
역전파 연산을 수행하기 위해 순전파 연산 중 나오는 중간 계산결과를 저장해야 할 때가 있다.
예를 들어 $f(x) = x^{2}$ 같은 함수의 경우, 그래디언트를 구하기 위해 입력 $x$를 저장해두어야 한다.
파이토치는 이럴 때 자동으로 텐서를 저장해준다!
x = torch.randn(5, requires_grad=True)
y = x.pow(2)
print(y)
print(x)
print(y.grad_fn._saved_self) # saved tensortensor([0.1810, 0.9848, 0.6616, 2.7275, 0.1596], grad_fn=<PowBackward0>)
tensor([-0.4254, -0.9924, -0.8134, 1.6515, -0.3996], requires_grad=True)
tensor([-0.4254, -0.9924, -0.8134, 1.6515, -0.3996], requires_grad=True)
미분불가능한 함수의 그래디언트
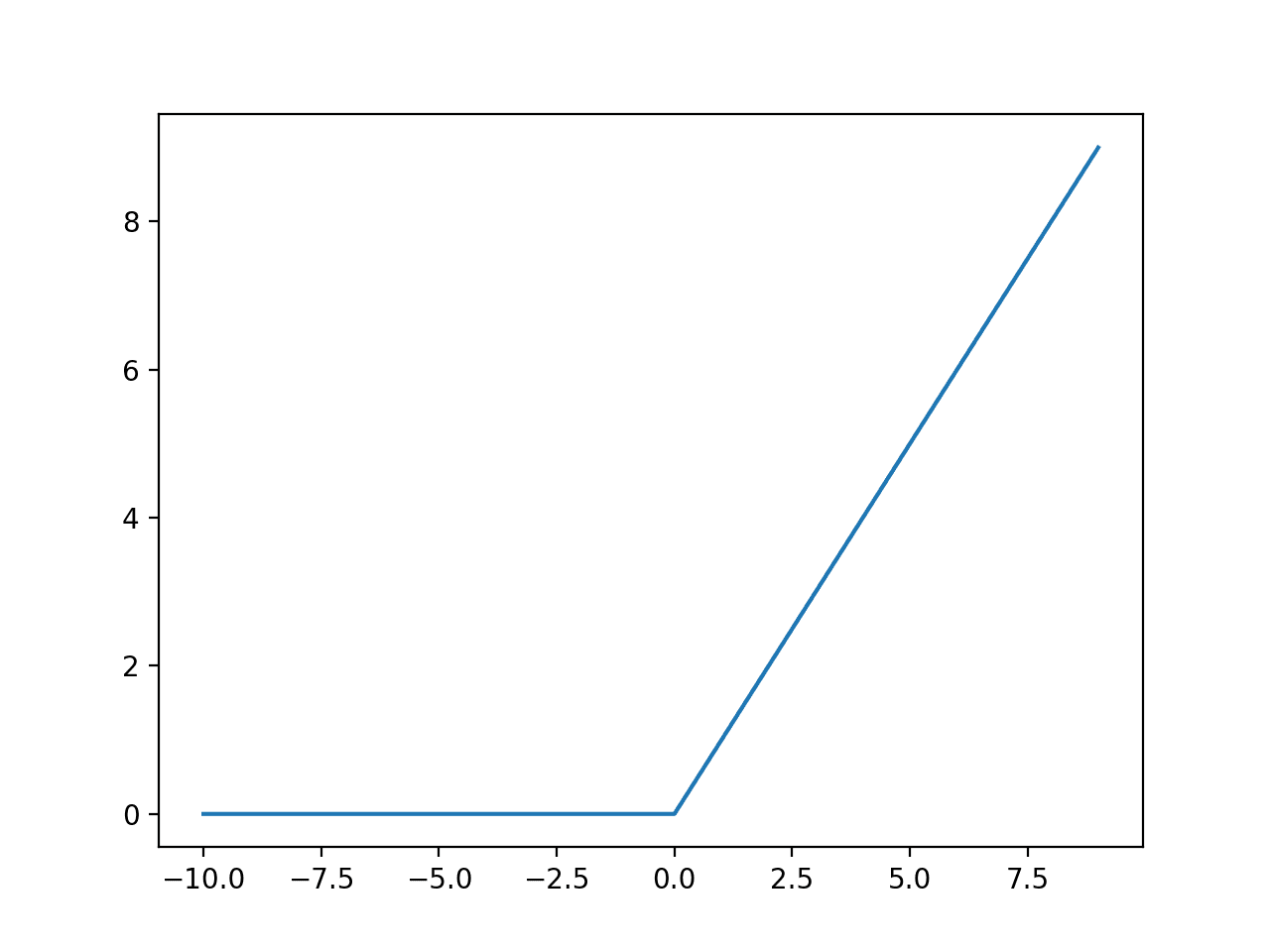
영점에서의 relu와 같이, 실세계에서 마주치는 많은 함수가 미분불가능한 함수다.
이러한 문제에 대해서 파이토치는 아래와 같은 원칙에 따라 그래디언트를 계산한다.
1. 함수가 미분가능하고 현재 지점의 그래디언트가 존재한다 -> 자동미분을 쓴다
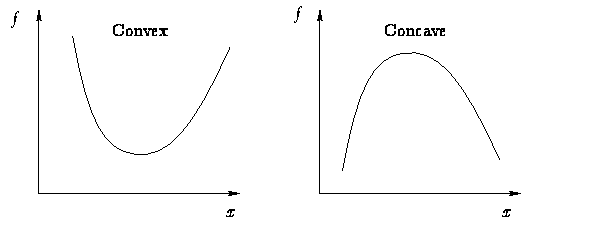
2. 함수가 (지역적으로라도) convex 하다 -> minimum norm의 sub-gradient(하위 미분)을 사용한다 (가장 가파른 하강 방향으로)
3. 함수가 (지역적으로라도) concave 하다 -> minimum norm의 super-gradient을 사용한다 ($-f(x)$를 고려)
4. 함수가 정의되어 있다 -> 연속성으로써 현재 지점의 그래디언트를 정의한다
- sqrt(0)과 같이 inf 는 가능하다고 본다
- 다양한 값을 쓸 수 있다면, 임의로 하나를 고른다
5. 함수가 정의되어 있지 않다 (sqrt(-1), log(-1), 혹은 입력이 NaN인 함수) -> 임의의 값 혹은 NaN을 그래디언트로 쓴다
6. 함수가 deterministic mapping가 아니다 -> 미분불가능하므로 에러
'인공지능 > 머신러닝-딥러닝' 카테고리의 다른 글
| 파이토치(PyTorch) 이해하기 with MNIST (0) | 2022.11.24 |
|---|---|
| 텐서플로우(TensorFlow)에서 파이토치(PyTorch)로 환승하기 (1) | 2022.11.24 |
| ASAM (pending) (0) | 2022.08.10 |
| tensorflow - 함수들 (0) | 2022.08.10 |
| Tensorflow (0) | 2022.08.10 |