
덧셈? a + b = c, 즉 두 개의 입력을 받아 c 를 출력하게 함
1. 칩에 대한 진리표를 만든다
2. 진리표를 수식으로 만든다
3. 수식을 논리게이트로 표현한다
[칩에 대한 진리표를 만든다]
덧셈을 진리표 형식으로 나타내기
| A | B | C |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 |
bit로는 마지막 행을 표현할 수가 없음
---> '자리올림'으로 해결

ㄴ 위 그림을 열별로 보았을 때 덧셈을 두번 시행했다고 볼 수 있음

ㄴ (자리올림값) + a + b = c 로 된 계산이 두번 시행된 것
따라서 가산기의 모양은 아래와 같이 됨

input은 세 개 : A, B, Ci (자리올림)
output은 두 개: Sum, Co (다음 자리올림에 올라갈 값)
Co 값은 새로운 가산기의 Ci 값이 됨

위 가산기의 진리표를 그려보기
| input | output | |||
| A | B | Ci | Co | Sum |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
[진리표를 수식으로 만든다]
사실은 ... Adder는 두 개의 칩으로 이루어진 것이다. output이 두 개(Co, Sum)이기 때문!
하나의 칩은 하나의 output을 가진다고 보면 된다
먼저, Co 에 대한 수식을 만들어보자
- 진리표에서 Co이 1이 되는 행을 찾는다
- Co 이 참이 될 때는?
- A는 거짓이고 B가 참이고, C도 참인 경우
혹은
- A가 참이고, B가 거짓이고, C도 참인 경우
혹은
- A가 참이고, B가 참이고, C는 거짓인 경우
혹은
- A가 참이고, B가 참이고, C가 참인 경우
--> 이를 수식으로 나타내면 (Ac∩B∩C)∪(A∩Bc∩C)∪(A∩B∩Cc)∪(A∩B∩C)
--> 이를 단순화하면 (A∩B)∪(B∩C)∪(A∩C)
(계산 과정)

[수식을 논리게이트로 표현한다]
(A∩B)∪(B∩C)∪(A∩C)
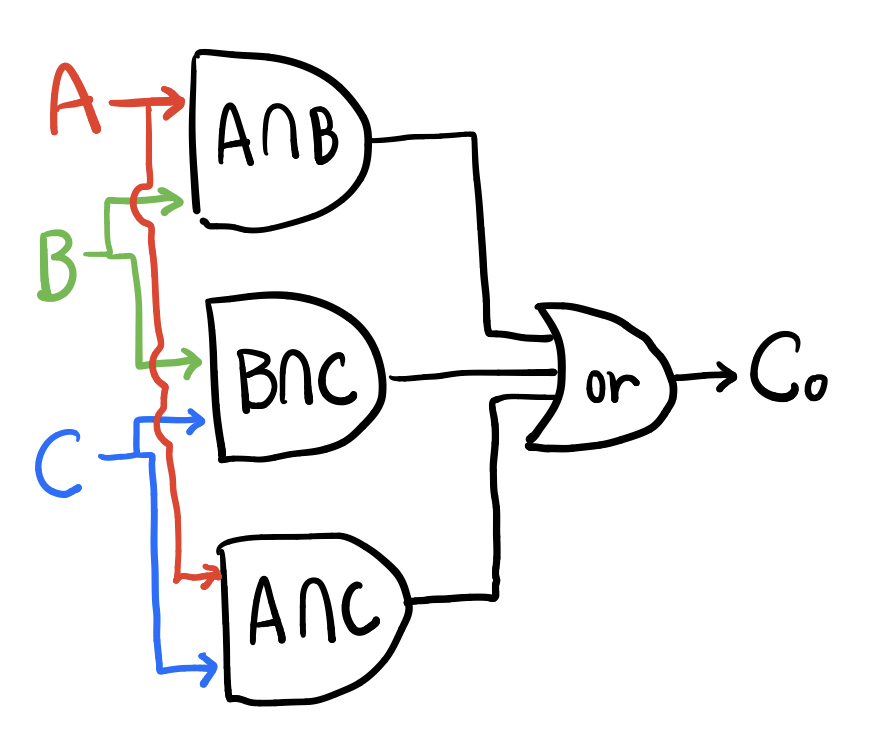
이상 Co칩을 논리게이트로 표현했다
같은 방식으로 Sum칩을 표현한다면?
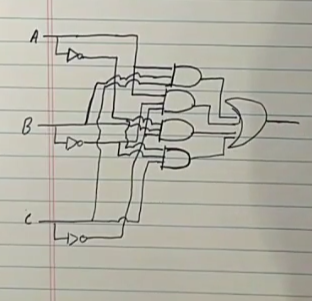
드디어 두 칩을 활용해서 Adder(가산기) 만들기
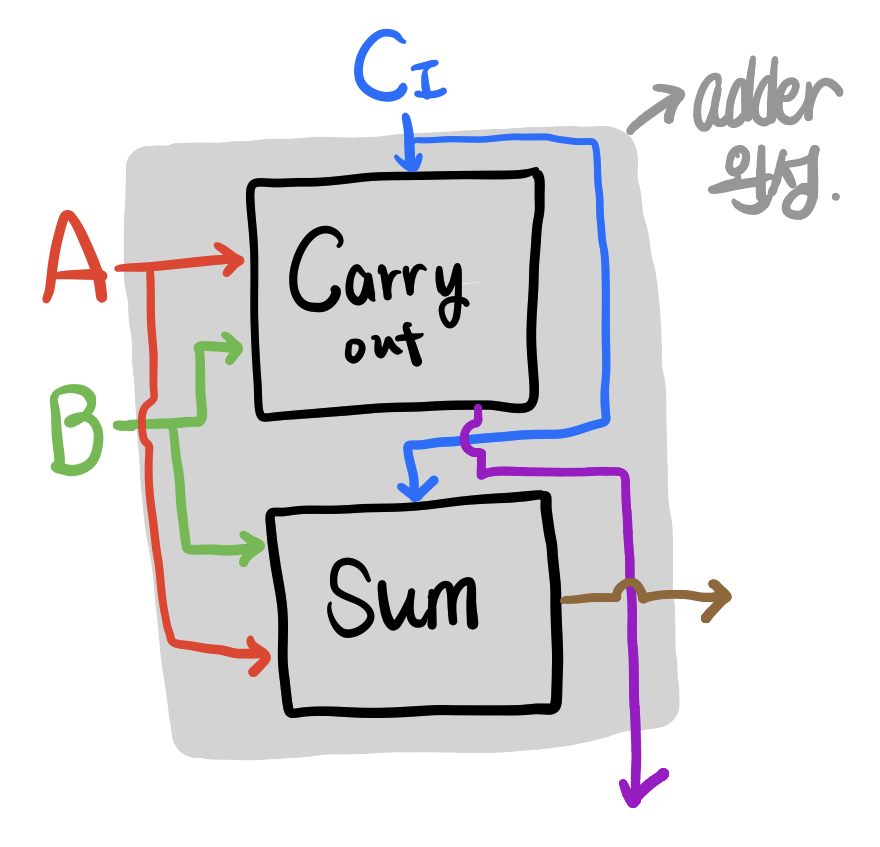
다만 위 가산기는 1bit 연산밖에 되지 않음
만약 1비트 이상의 연산을 하고자 한다면? 예를 들어 3비트 연산
열 방향으로 보았을 때 가산기 세 개가 존재하는 것임
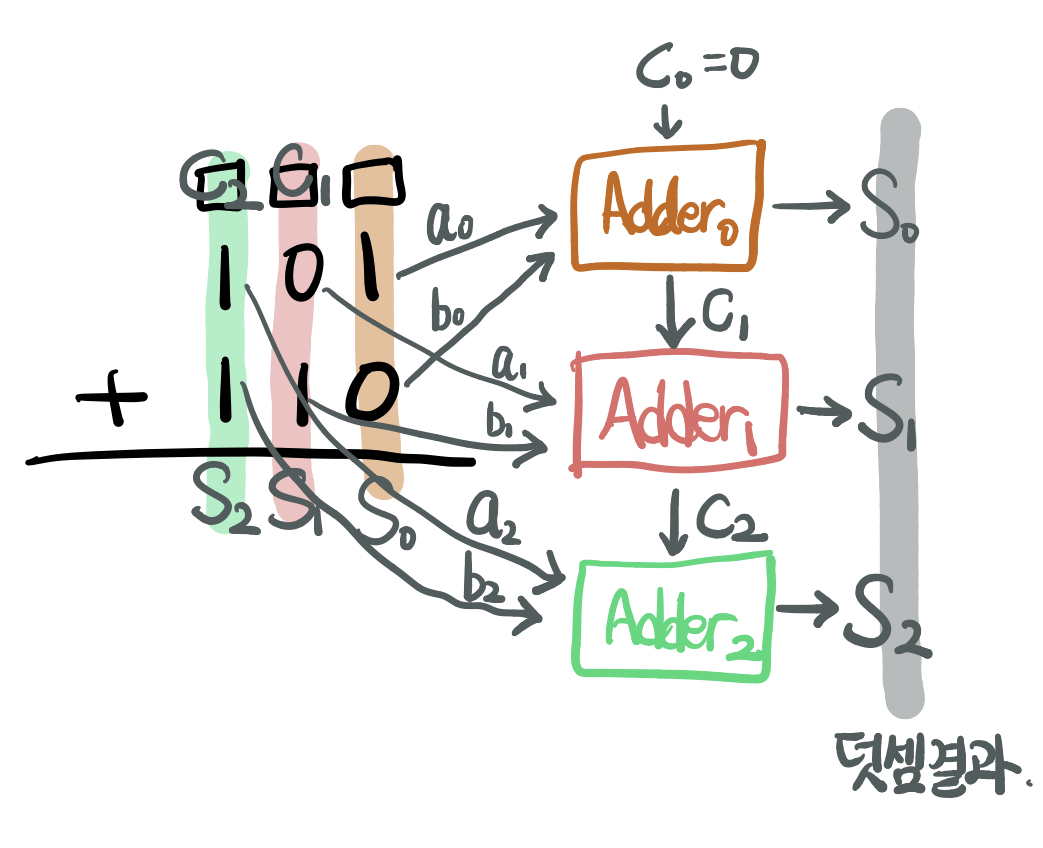
앞 연산들이 모두 끝나야 다음 연산이 가능하다는 단점 ---> 1비트 연산에 비해 3비트 연산이 3배의 시간이 걸리게 됨
이와 같이 Carry가 물방울 뚝뚝 떨어지듯 연산이 이루어지는 '리플 캐리 방식'이 실제로 쓰이지 않음
따라서 '캐리 룩어헤드' 방식을 사용하게 됨: 캐리값이 한꺼번에 계산이 되어 Sum값이 한번에 계산이 되는 시스템
추가 자료: https://opentutorials.org/module/2719/15502
'컴퓨터 > BASIS' 카테고리의 다른 글
| git branch 트리 구조를 보기 좋은 형태로 열람하기 (0) | 2024.08.08 |
|---|---|
| tmux - 원격으로 접속하기 (0) | 2022.08.11 |
| 컴퓨터 밑바닥부터 이해하기(1) (0) | 2022.05.10 |
| [Git] git을 통한 협업 (0) | 2022.01.01 |
| 나를 늘 삽질하게 만드는 git (0) | 2021.09.29 |