
Derivatives
미적분을 직관적으로 이해하기!

$a = 2$ 일 때, $f(a) = 6$
$a = 2.001$ 일 때, $f(a) = 6.003$
밑변이 $0.001$ 이고, 높이가 $0.003$인 삼각형이 생긴다
따라서 $a=2$에서의 $f(a)$의 미분값은 $3$이다 (= $\frac{height}{width} = \frac{0.003}{0.001}$)
같은 원리로 $a=5$에서의 $f(a)$의 미분값 $3$이다
$ \frac{df(a)}{da} = \frac{d}{da}f(a) = 3$
미분의 formal definition 에서는 0.001보다 훨씬 (거의 무한대로) 작은 값을 사용
위 함수는 $a$의 값과 상관없이 항상 같은 slope를 가진다
More Derivative Examples
slope 가 변화하는 경우!
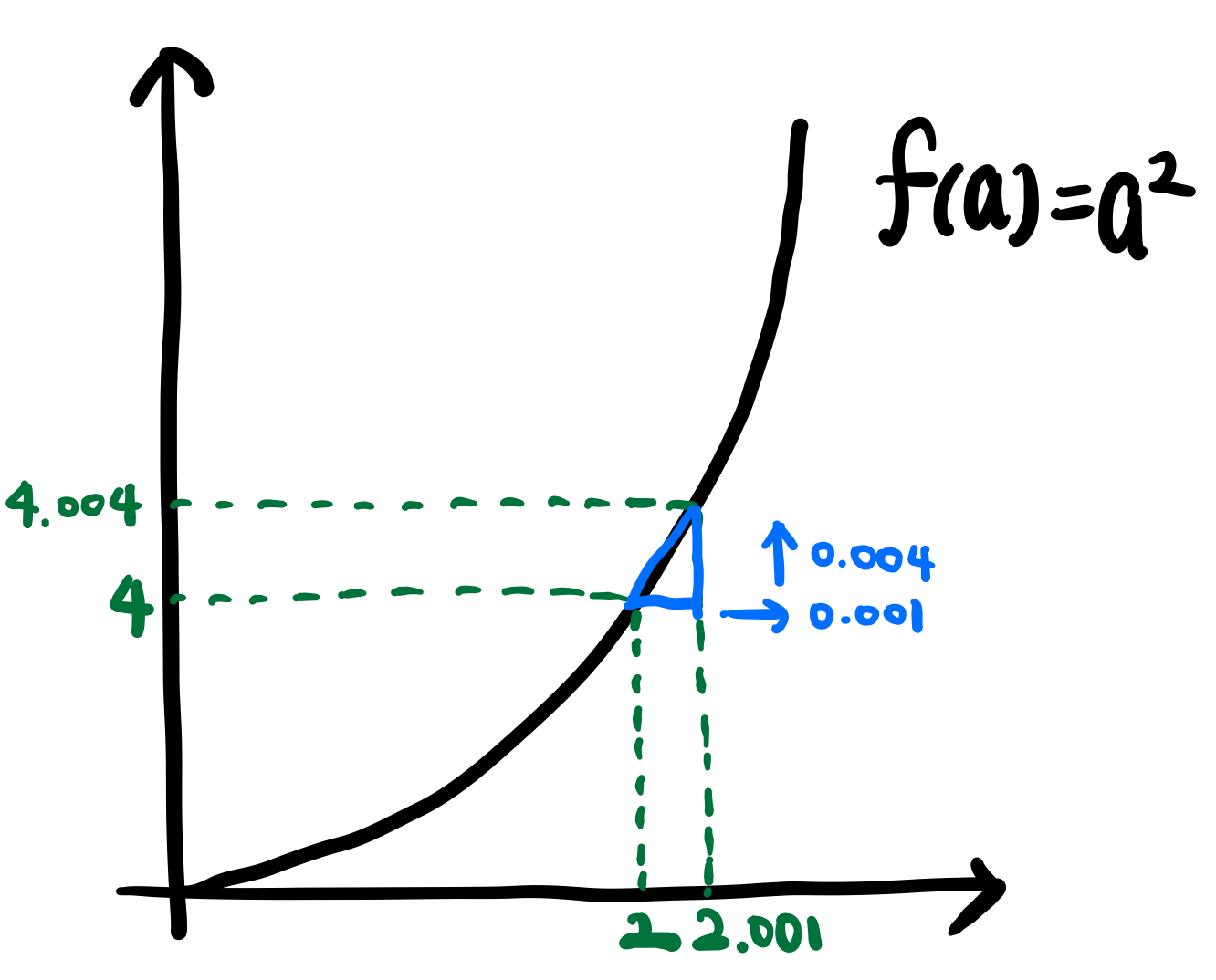
$a = 2$ 일 때, $f(a) = 4$
$a = 2.001$ 일 때, $f(a) \approx 4.004$
따라서
$a = 2$ 일 때, $ \frac{d}{da}f(a) = 4$
그러나
$a = 5$ 일 때, $f(a) = 25$
$a = 5.001$ 일 때, $f(a) \approx25.010$
따라서
$a = 5$ 일 때, $ \frac{d}{da}f(a) = 10$
즉 미분값이 커짐
왜 미분값이 달라지나? 점마다 $\frac{height}{width}$가 달라지기 때문
식으로 나타내면
$ \frac{d}{d}a^{2} = 2a$
* $a = 2.001$ 일 때, $f(a) \approx 4.004$ 라고 했지만 사실은 $4.004001$ 임
$0.001$만큼 이동했기 때문에. 미분에서는 무한대로 작은 수만큼 이동한다고 봄.
[More derivative examples]
$f(a) = a^{3}$ 이면 $\frac{d}{da} f(a) = 3a^{2}$
$f(a) = \log (a)$ 라고 해보자. ($\log_{e} (a)$, 즉 $\ln (a)$)
이 경우, $\frac{d}{da} f(a) = \frac {1}{a}$
'인공지능 > DLS' 카테고리의 다른 글
| [1.3.] Shallow Neural Networks(1) (0) | 2022.06.26 |
|---|---|
| [1.2.] Neural Networks Basics - Python and Vectorization (0) | 2022.06.26 |
| [1.2.] Neural Networks Basics - Logistic Regression as a neural network(3) (0) | 2022.06.26 |
| [1.2.] Neural Networks Basics - Logistic Regression as a neural network(1) (0) | 2022.06.24 |
| [1.1.] What is a Neural Network? (0) | 2022.06.24 |