
What is Neural Style Transfer?

Content image ($C$), Style image($S$), Generated image($G$)
What are deep ConvNets learning?
[Visualizing what a deep network is learning]

Pick a unit in layer 1. Find the nine image patches that maximize the units activation
특정 unit의 활성화값을 극대화한 이미지(패치)가 무엇인가?
- hidden unit in layer 1 will see only a relatively small portion of the neural network

- if you plot what activated unit's activation, it's just small image patches - all of the images that that particular unit sees
- 위 패치들은 '\' 이렇게 생긴 edge들
하나의 hidden unit's activation을 극대화하는 이미지 패치 9개
- Repeat for other units
input region = receptive field

- layer 1의 hidden unit들은 주로 edge나 색깔 같은 단순한 feature 를 주로 본다는 것을 알 수 있음
- 보다 깊은 레이어의 unit을 시각화하면 어떻게 될까?
- 후반의 unit들은 좀더 큰 이미지 패치를 본다

레이어별로 9개 hidden unit - unit 별로 9개 이미지 패치
단순한 패턴을 찾던 초반 레이어 - 레이어가 깊어질수록 복잡한 object를 detect할 수 있게 됨
Cost Function
[Neural style transfer cost function]
gradient descent로 $J(G)$ 최적화 : 생성된 이미지($G$)가 얼마나 좋은지 어떻게 정의할 수 있을까?
$$J(G) = \alpha J_{content}(C, G) + \beta J_{style}(S, G)$$
- $J_{content}(C, G) $: $C$와 $G$의 content가 얼마나 유사한지
- $J_{style}(S, G)$ : $S$와 $G$의 style이 얼마나 유사한지
- $\alpha$, $\beta$ : 가중치
[Find the generated image G]
1. $G$를 랜덤하게 초기화한다
- $G$ : 100 x 100 x 3 (RGB)
2. $J(G)$를 최소화하기 위해 gradient descent 를 사용한다
- $G := G - \frac{\partial}{\partial G} J(G)$
- $G$의 픽셀값을 업데이트한 것
Content Cost Function
$$J(G) = \alpha J_{content}(C, G) + \beta J_{style}(S, G)$$
- content cost 를 구하기 위해 hidden layer $l$개를 사용한다고 가정
(ex. 레이어 깊어질수록 .. "content 이미지에 강아지 있으니까 강아지도 포함하셈")
- 신경망이 너무 얕거나 깊지 않도록 해야 함
- pretrained ConvNet 이용
- 주어진 content 이미지와 generated 이미지의 content가 얼마나 비슷한지 계산
- $a^{[l](C)}$, $a^{[l](G)}$: 이미지 $C$, $G$의 $l$번째 레이어의 활성화값
- 두 값이 비슷하면 비슷한 content를 가지고 있다고 본다
$$J_{content}(C,G) = \parallel a^{[l](C)}- a^{[l](G)} \parallel^{2}$$
- element-wise sum of square differences 구함
---> 두 값은 vector로 unroll 된 상태
Style Cost Function
[Meaning of the "style" of an image]

$l$번째 레이어의 활성화값을 활용해 "style"을 측정할 수 있다 (화살표가 $l$번째 레이어라고 해보자)
채널들에 걸친 활성화값들 사이 상관관계(correlation between activations across channels)를 "style"로 정의한다
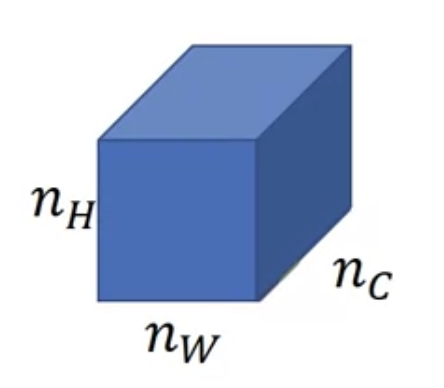
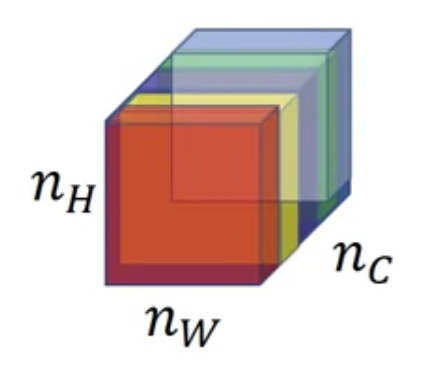
How correlated are the activations across different channels?
예를 들어 빨간색 채널에서 특정 위치의 값과, 같은 위치이되 노란색 채널일 때의 값 사이 correlation을 구할 수 있다
이렇게 두 값을 쌍으로 묶어 모든 위치에 대해서 correlation을 구한다
-> 이것을 style로 볼 수 있는 이유는 무엇일까?
[Intuition about style of an image]
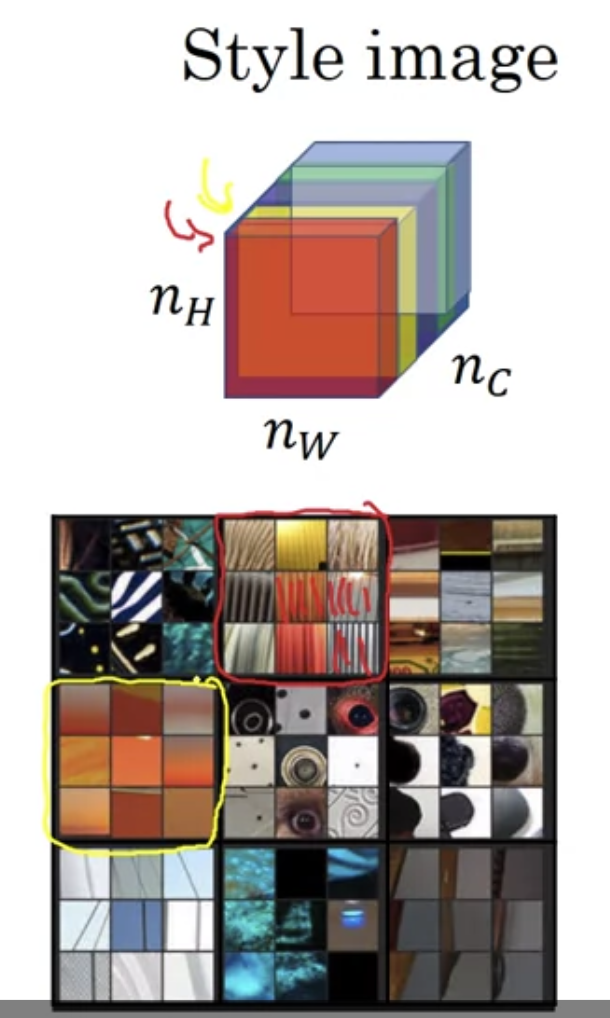
채널별로 시각화된 이미지를 보자. 빨간 박스(vertical lines들 포착)는 빨간색 채널, 노란 박스(주황색 느낌 포착)는 노란색 채널.
두 채널이 "highly correlated"되었다는 것은 무슨 의미일까? vertical texture를 가진 이미지는 주황색 느낌도 날 것임
"uncorrelated"되었다는 것은? vertical texture를 가진 이미지가 주황색 느낌이 나지 않을 것임
the correlation tells you which of these high level texture componetns tend to occur or not occur together in part of an image
이를 이용해서 style image 와 생성된 이미지의 style이 얼마나 유사한지 계산할 수 있음
[style matrix]
- $a_{i,j,k}^{[l]}$ = activation at $(i, j, k)$
- $i$ : 높이(height)
- $j$ : 가로(width)
- $c$ : k번째 채널
- style matrix $G^{[l]}$ : $n_{c}^{[l]} \times n_{c}^{[l]}$ 차원의 행렬
- $n_{c}$개 채널이 있을 때, 각 쌍의 상관관계를 구하기 위해서는 $n_{c}^{[l]} \times n_{c}^{[l]}$ 차원의 행렬이 필요하다
- $G_{k, k'}^{[l]}$ : $k$번 채널과 $k'$번 채널의 상관관계를 계산
- $k = 1, \cdots, n_{c}^{[l]}$ : 1부터 $l$번째 레이어의 채널 개수까지
$$G_{k, k'}^{[l]} = \sum_{i=1}^{n_{H}^{[l]}} \sum_{j=1}^{n_{W}^{[l]}} a_{i,j,k}^{[l]} a_{i,j,k'}^{[l]}$$
- $k$번째 채널과 $k'$번째 채널의 모든 위치의 활성화값 쌍을 곱한다
- 상관관계 있을수록 곱한 값은 커지고, 없을수록 작아진다
쉬운 이해를 위해 상관관계(correlation)라고 불렀는데, 사실은 unnormalized cross-covariance 이다 (평균 빼는 과정 없이 바로 곱하기 때문에 unnormalized)
style 이미지(S), 생성된 이미지(G) 모두에 대해 계산을 한다. 즉,
$$G_{k, k'}^{[l](S)} = \sum_{i=1}^{n_{H}^{[l]}} \sum_{j=1}^{n_{W}^{[l]}} a_{i,j,k}^{[l](S)} a_{i,j,k'}^{[l](S)}$$
$$G_{k, k'}^{[l](G)} = \sum_{i=1}^{n_{H}^{[l]}} \sum_{j=1}^{n_{W}^{[l]}} a_{i,j,k}^{[l](G)} a_{i,j,k'}^{[l](G)}$$
style matrix $G$는 선형대수학에서 "gram matrix"라고 부르는 것임
정리해보자면
$$J_{style}^{[l]}(S, G) = \frac{1}{(\cdots)} \parallel G^{[l](S)} - G^{[l](G)} \parallel_{F}^{2} $$
$$= \frac{1}{(2n_{H}^{[l]}n_{W}^{[l]}n_{c}^{[l]})^{2}}\sum_{k}\sum_{k'}(G_{kk'}^{[l](S)} - G_{kk'}^{[l](G)})^{2}$$
앞에 붙은 normalization 상수는($\frac{1}{(2n_{H}^{[l]}n_{W}^{[l]}n_{c}^{[l]})^{2}}$) 큰 상관 없음
- Frobenius norm
- 여러 레이어에 걸쳐 계산한 값까지 모두 더하여
$$J_{style}(S, G) = \sum_{l} \lambda^{[l]}J_{style}^{[l]}(S, G)$$
$$J(G) = \alpha J_{content}(C, G) + \beta J_{style}(S, G)$$
1D and 3D generalizations

1D 데이터에도 conv 연산이 가능하다 - 1D 데이터는 보통 RNN, LCM 같은 모델을 쓰긴 함
한편 3D 데이터
CT 촬영 데이터는 3D 데이터 - 몸을 지나면서 slices of images(depth) 를 가지고 있음
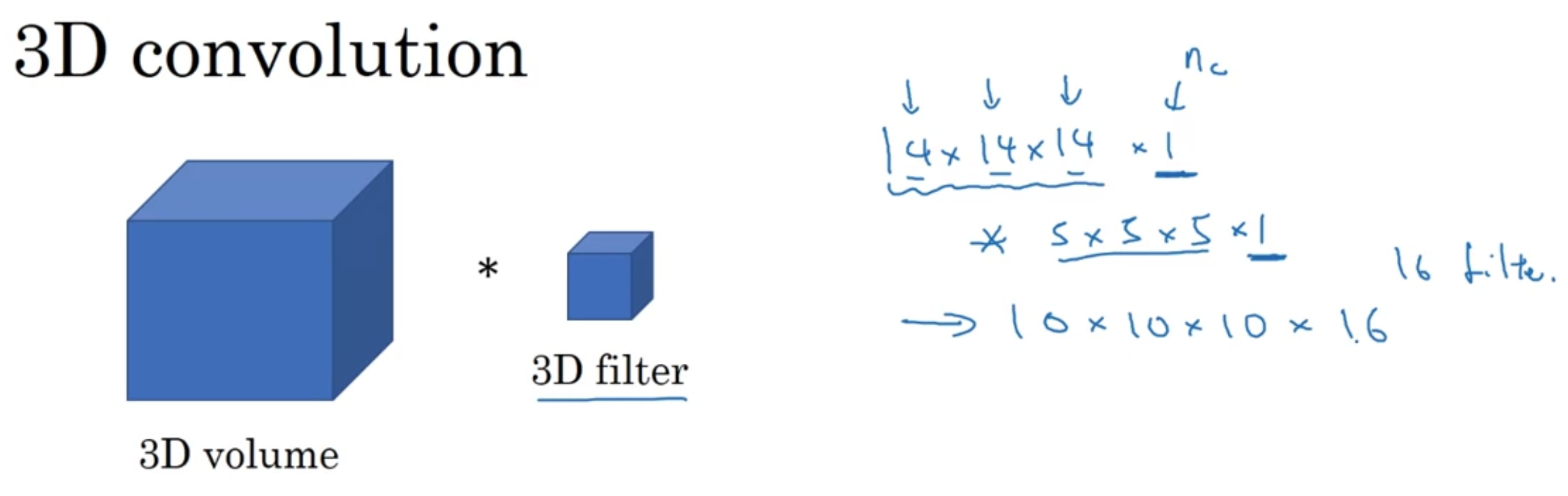
conv 연산 똑같이 하되 차원이 하나 더 추가되었을 뿐
영화 장면도 3D data 라고 볼 수 있음
'인공지능 > DLS' 카테고리의 다른 글
| [5.1.] Recurrent Neural Networks(2) (0) | 2022.08.02 |
|---|---|
| [5.1.] Recurrent Neural Networks(1) (0) | 2022.08.02 |
| [4.4.] Face Recognition (0) | 2022.08.02 |
| [4.3.] Detection Algorithms(3) (0) | 2022.08.02 |
| [4.3.] Detection Algorithms(2) (0) | 2022.08.01 |