Word Representation

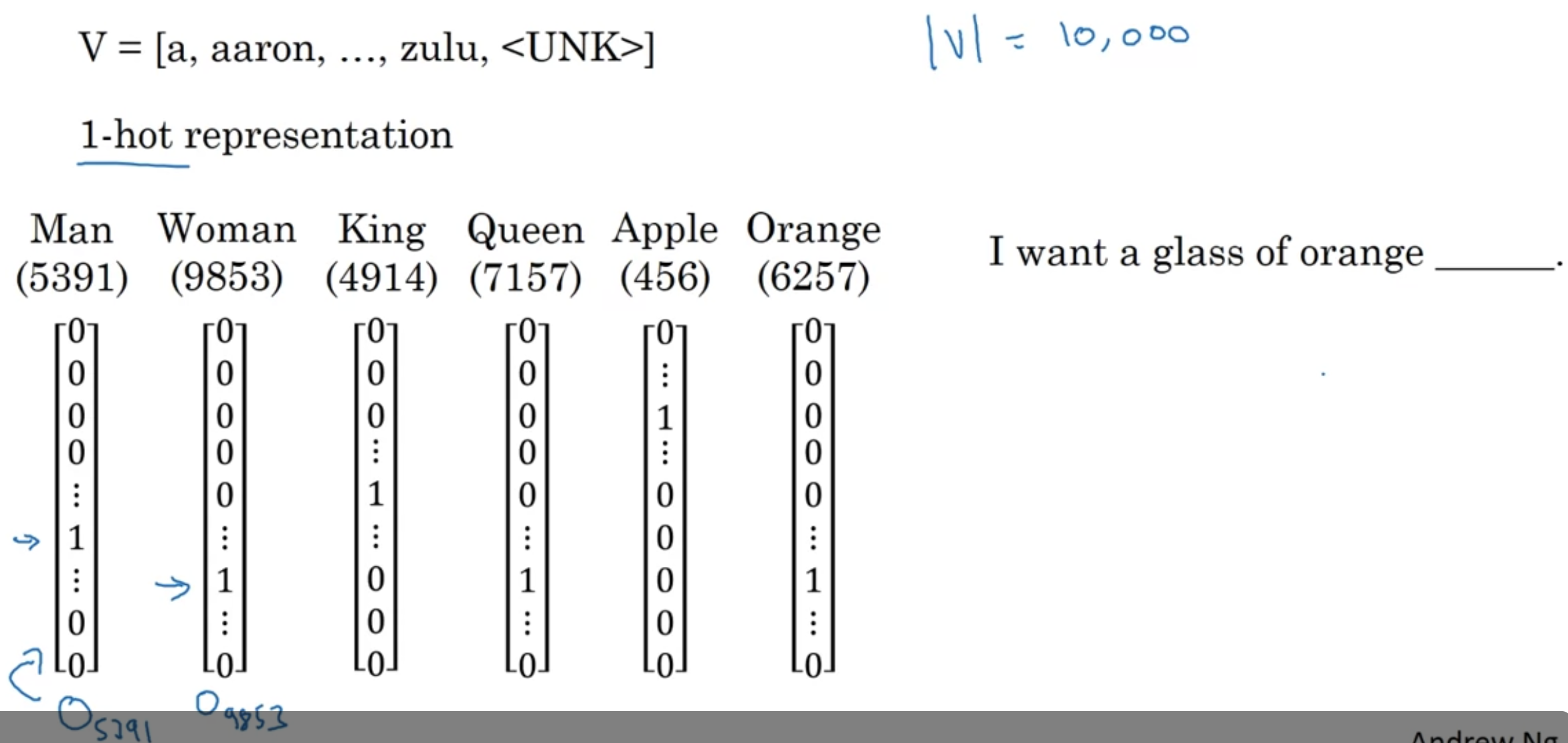
지금까지는 Vocab 사용해서 (위 예시의 경우 사이즈가 10,000) one-hot vector로 단어를 표현했음
예를 들어 Orange가 vocal에서 6257번째 단어라면 $O_{6257}$로 표기
이러한 representation의 단점

- 이러한 예시에서 orange와 apple이 가까운 관계에 있다는 것을 학습하지 못함
--> 두 개의 다른 one-hot vector의 내적(inner product)은 $0$이기 떄문
one-hot representation 대신에 "featurized representation"을 사용해보자!
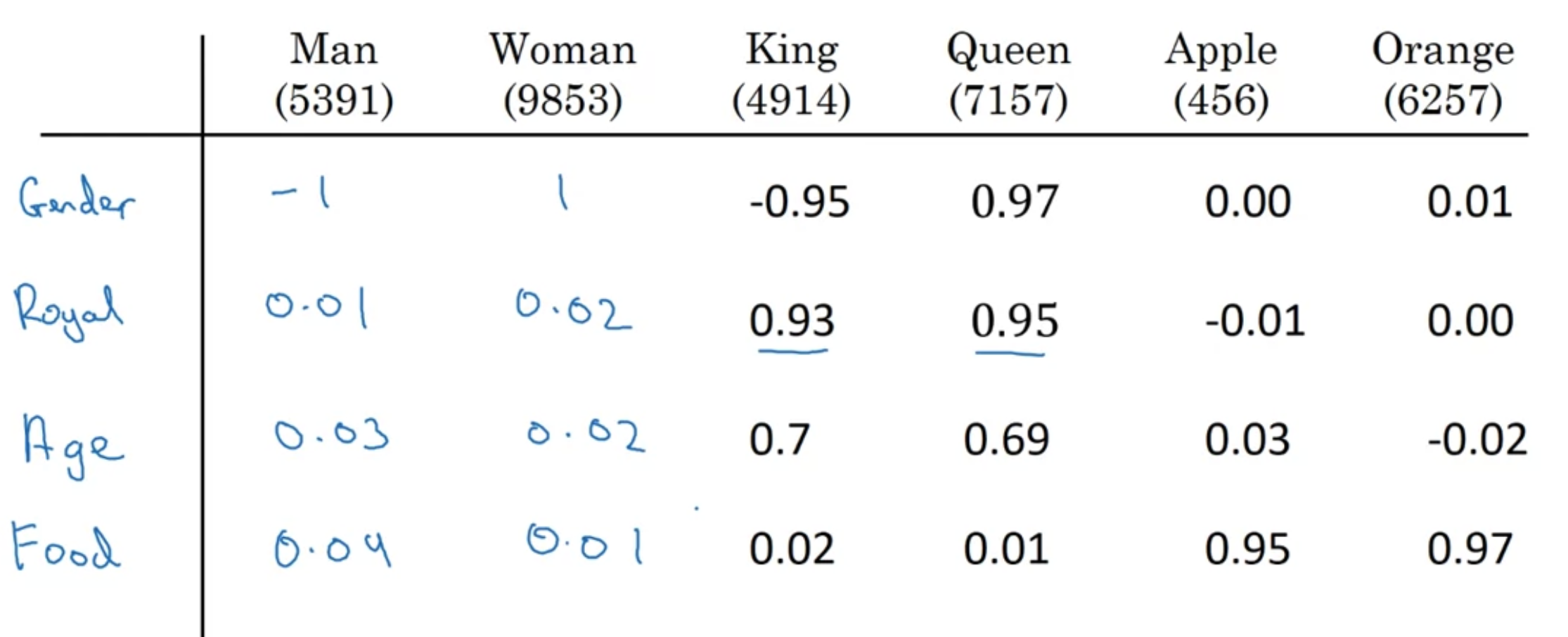
그 외에 size, cost, alive, verb .. 등등 다양한 feature 생각해볼 수 있음
예를 들어 300개의 feature가 있다고 해보자
그러면 "Man"을 represent하는 300차원의 벡터가 생긴다 -> $e_{5391}$ 로 표현하기로 함
이제 orange와 apple이 비슷하다는 것을 알 수가 있다; 많은 feature에 있어서 같은/비슷한 값으로 표현되기 때문
this allows the algorithm to generalize better across different words
실제로 학습된 feature들이 gender를 의미하는지 royal를 의미하는지 정확히 알아내기는 어려울 수 있음
[Visualizing word embeddings]
300차원으로 표현된 단어들을 2차원 시각화하기
자주 사용하는 알고리즘 중 하나는 t-SNE
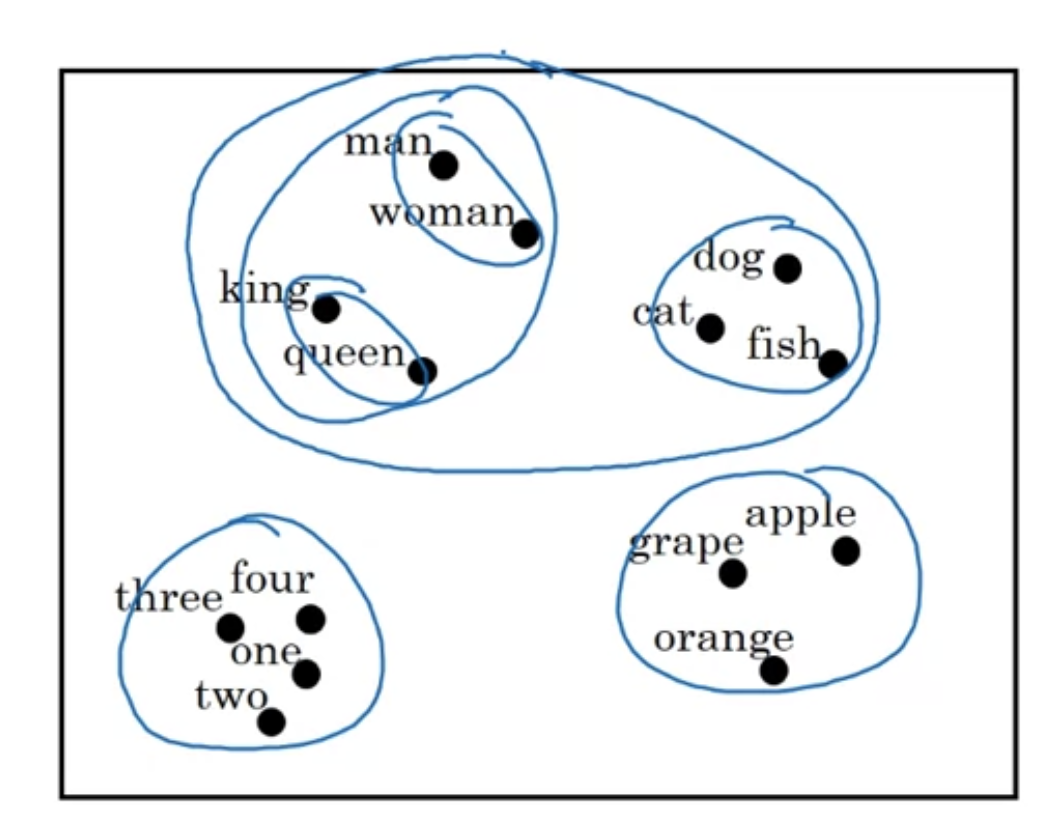
"embeddings"
300차원의 한 지점에 단어가 embeded 된다
Using Word Embeddings
[Named entity recognition example]
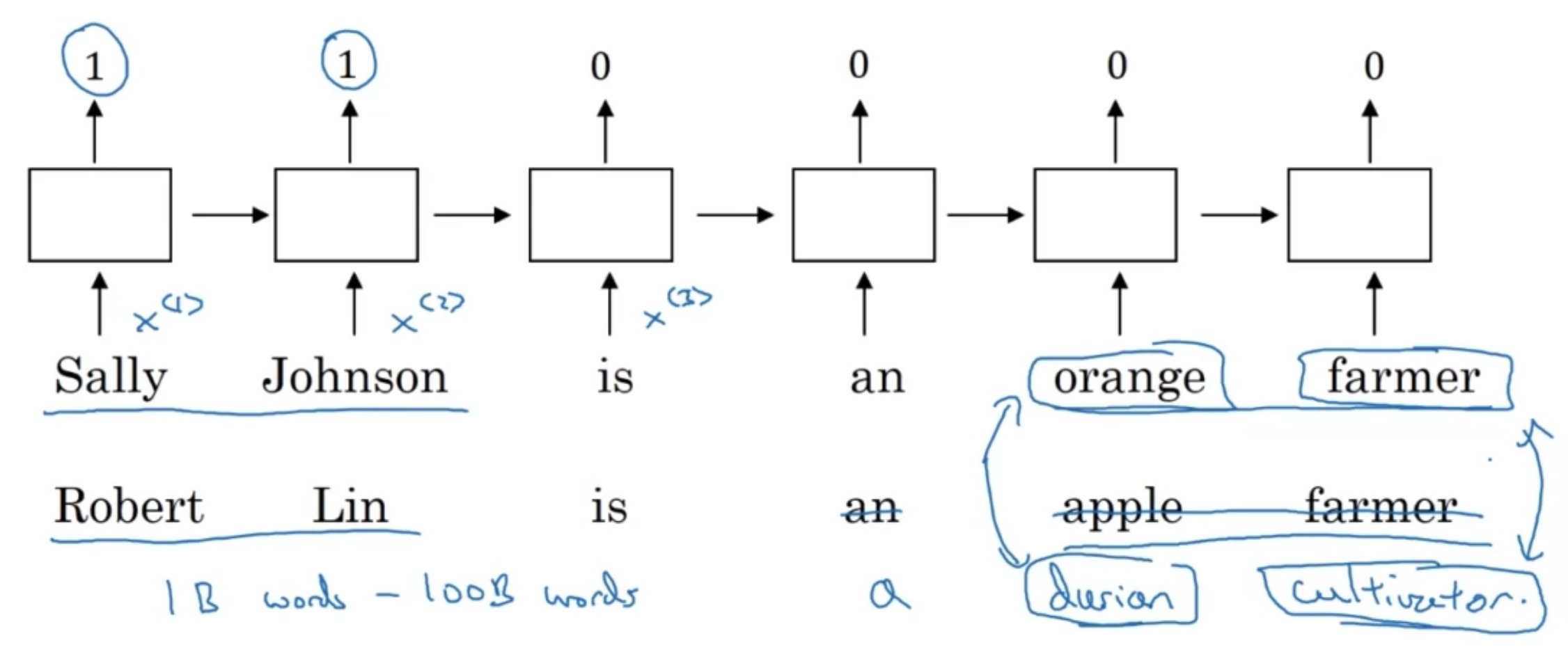
featurized representation 을 사용하면,
"orange farmer"와 "apple farmer"가 비슷한 단어라는 것을 알 수 있기 때문에 named entity 을 수행하는 데 유리
만약에 두번째 예시가 "Robert Lin is a durian cultivator"이고, 가지고 있는 비교적 작은 training set에 "durian", "cultivator" 라는 말이 없을 때는?
거대한 훈련셋(ex. 1B~100B의 인터넷 자료)에 훈련된 모델을 traing set으로 transfer learning 할 수 있음
[Transfer learning and word embeddings]

수행해야 할 task를 위한 학습셋이 비교적 작을 때 word embedding을 효과적으로 사용할 수 있다 (어떤 language modeling, machine translation 등 task에서는 그다지,)
transfer learning(A->B) 은 데이터A 크기가 매우 크고 데이터B의 크기가 상대적으로 적을 때 효과적
[Relation to face encoding]
- "encoding"과 "embedding"은 매우 비슷한 표현
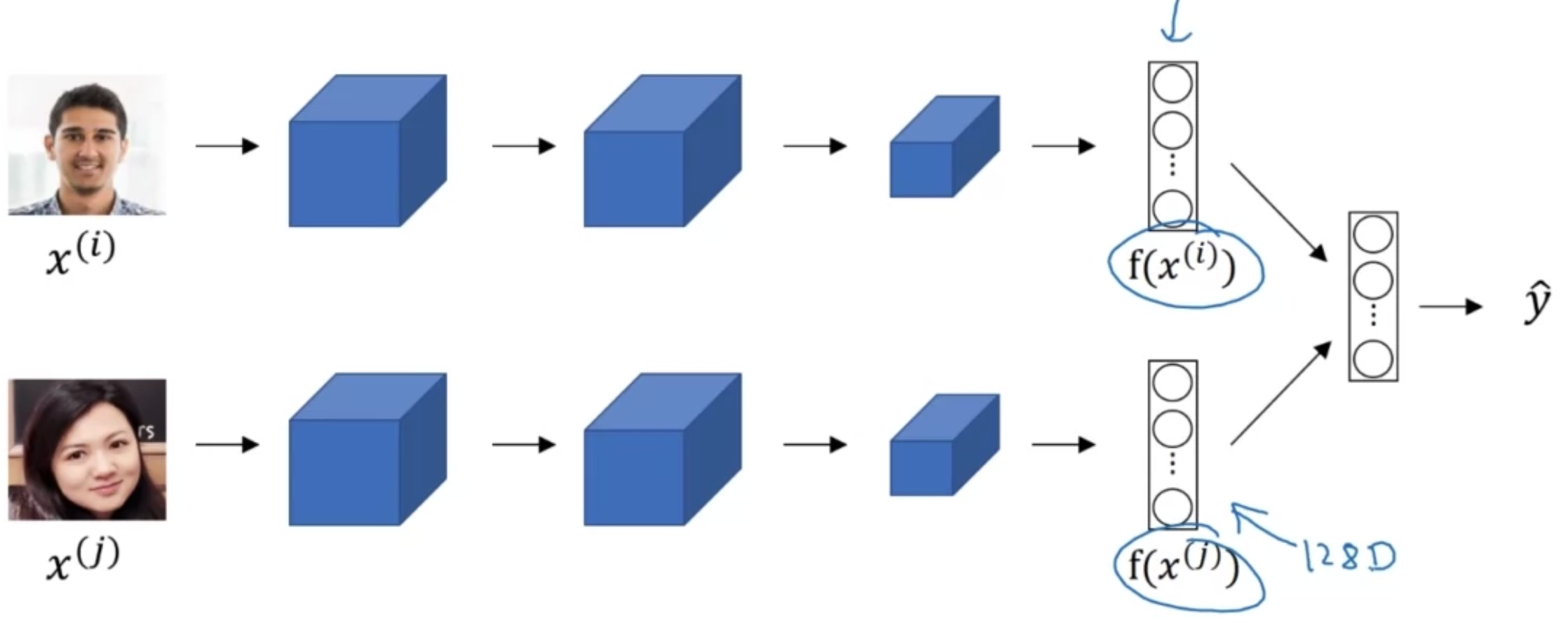
siamese 네트워크에서 두 얼굴을 비교할 때 사용하는 128차원의 face encoding
word embedding과 차이점은?
어떤 새로운 얼굴 이미지라도 CNN 네트워크를 통과하여 encoding할 수 있음
반면 word embedding은 고정된 크기의 vocab이 있고, 그 속의 각 단어에 대한 embedding을 학습하게 됨
Properties of Word Embeddings
- analogy reasoning
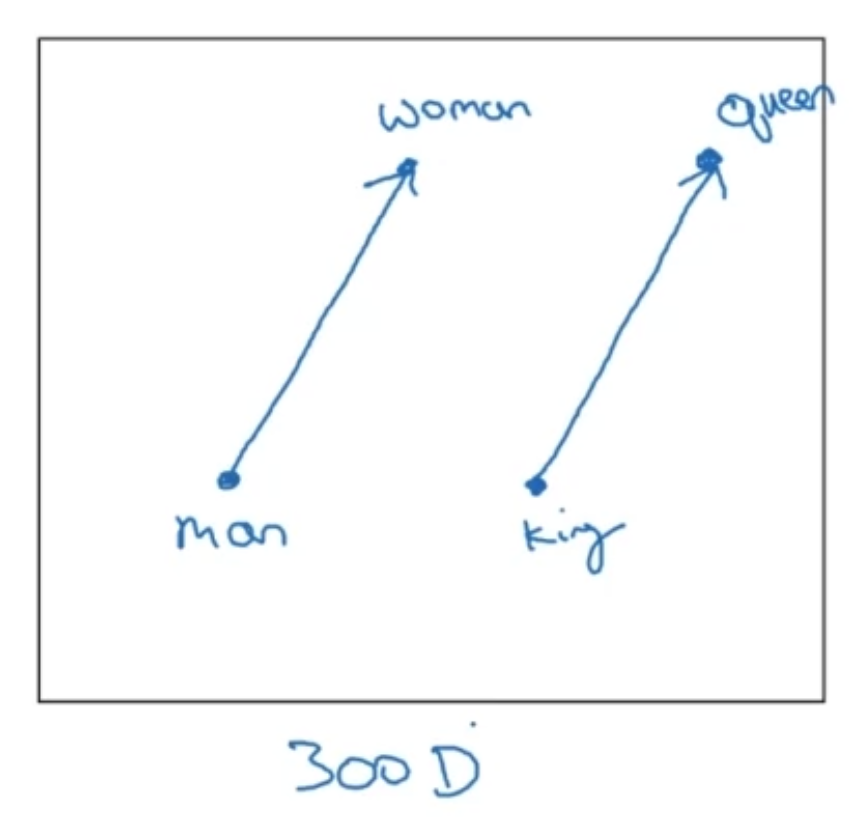
Man -> Woman
as
King -> ___?___
4차원의 word embedding으로 represent 한다고 쳤을 때,
$$e_{man} = \begin{bmatrix}-1\\0.01 \\0.03\\0.09\end{bmatrix} , \ e_{woman}= \begin{bmatrix}1\\0.02 \\0.02\\0.01\end{bmatrix}$$
$$e_{king} = \begin{bmatrix}-0.95\\0.93 \\0.70\\0.02\end{bmatrix} , \ e_{queen}= \begin{bmatrix}0.97\\0.95 \\0.69\\0.01\end{bmatrix}$$
$$e_{man} - e_{woman} = \begin{bmatrix}-2\\0 \\0\\0\end{bmatrix}$$
$$e_{king} - e_{queen} = \begin{bmatrix}-2\\0 \\0\\0\end{bmatrix}$$
- man과 woman의 주요 차이는 'gender'이고, king과 queen도 마찬가지다
- 따라서 벡터끼리 뺀 값의 결과가 같은 것임
[Analgoies using word vectors]
$$e_{man} - e_{woman}\approx e_{king} - e_{?}$$
위 식을 만족하기 위한 단어를 찾는다면
Find word $w$:
$$\mathop{argmax}_{w}\ sim(e_{w}, e_{king} - e_{man} + e_{woman})$$
- t-SNE: 300차원을 2차원에 비선형적인 방식으로 맵핑하기 때문에 바로 위에 보이는 300차원 시각화 이미지처럼 되지는 않음 (단어와 단어 관계가 평행으로 나타나는)
- 자주 사용하는 similarity function?
[cosine simliarity]
$$sim(u, v) = \frac{u^{T}v}{ \parallel u \parallel _{2} \parallel v \parallel _{2}}$$
분자만 보자면, 결국에 내적(inner prodcut)과 마찬가지인데 두 벡터가 비슷할수록 결과는 커지게 됨
- square similarity 도 있음
$$\parallel u-v \parallel ^{2}$$
하지만 similarity 보다는 dissimilarity 측정하는 데 더 적절함
코사인 유사도를 더 자주 사용함
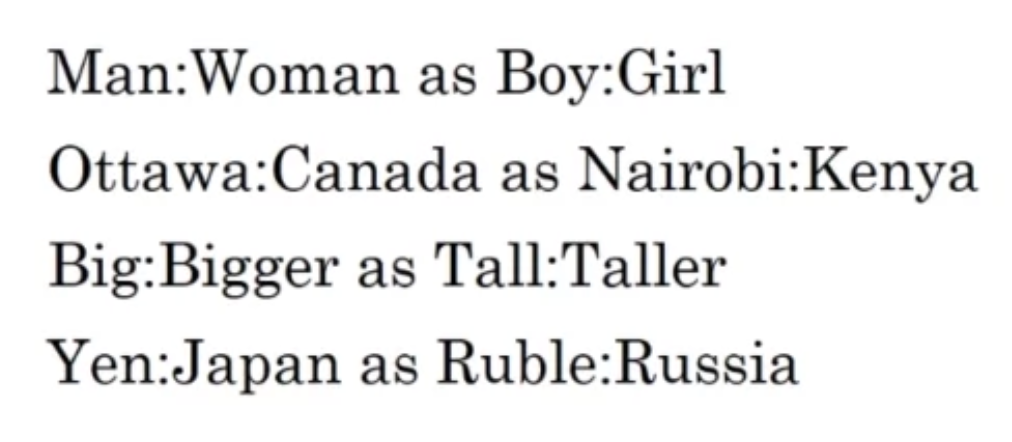
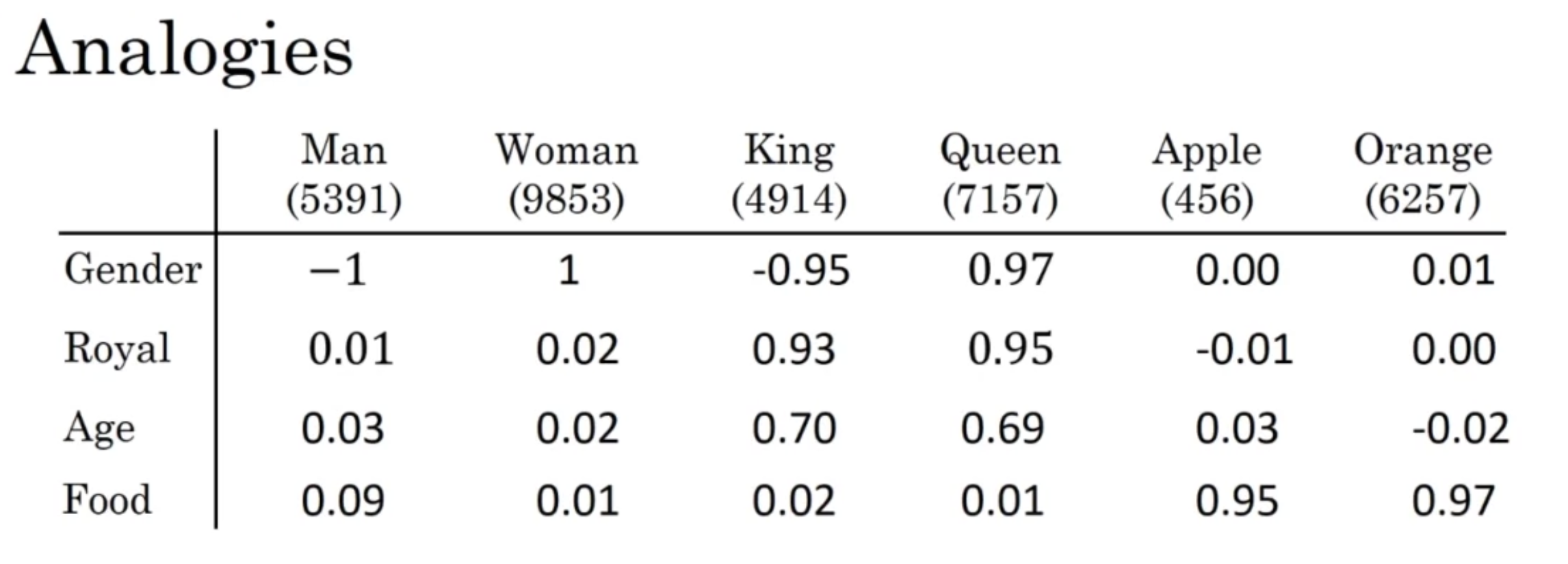
Embedding Matrix

사전에 있는 모든 단어의 featurized vector 를 가지고 하나의 embedding matrix 를 구성하기로 함
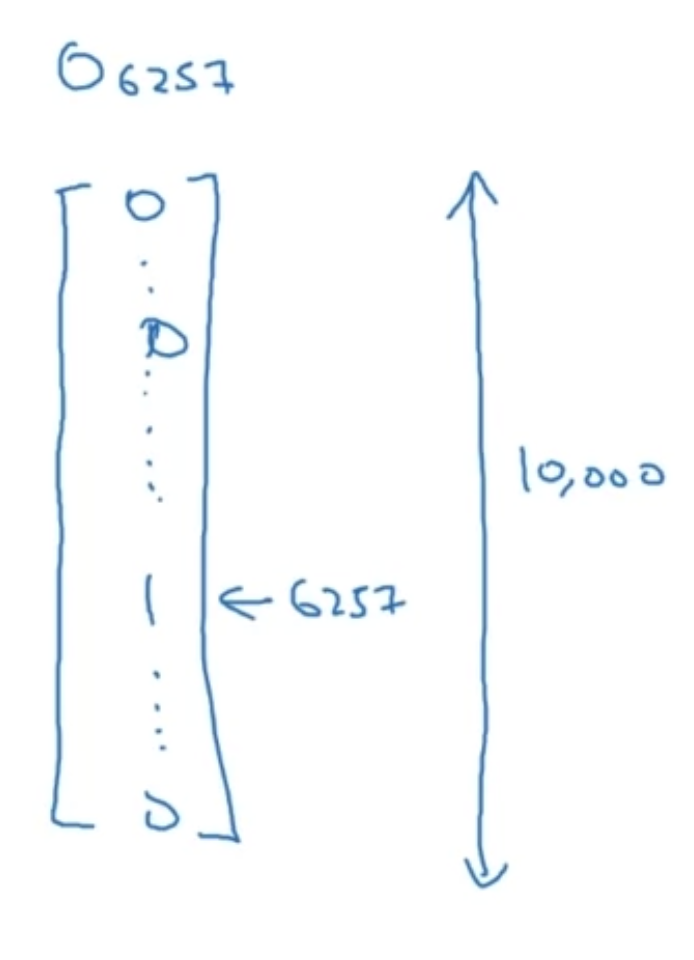
또 단어별로 one-hot vector 가 있음
위의 metrix $E$($(300, 10000)$ 차원)와 one-hot vector($(10000, 1)$ 차원)를 곱한다면
$$E \cdot O_{6257} = e_{6257}$$
그 결과는 $(300, 1)$ 차원의 벡터인 $e_{6257}$
'인공지능 > DLS' 카테고리의 다른 글
| [5.2.] Applications Using Word Embeddings (0) | 2022.08.11 |
|---|---|
| [5.2.] Learning Word Embeddings: Word2vec & GloVe (0) | 2022.08.09 |
| [5.1.] Recurrent Neural Networks(3) (0) | 2022.08.06 |
| [5.1.] Recurrent Neural Networks(2) (0) | 2022.08.02 |
| [5.1.] Recurrent Neural Networks(1) (0) | 2022.08.02 |