Vanishing Gradients with RNNs

"The cat, which already ate ... , was full"
"The cats, which already ate ..., were full"
-> long term dependency 를 가지는 경우
깊은 NN 모델이 vanishing gradient 문제를 겪었듯이, basic RNN 아키텍처 또한 backprop시 앞의 time step의 영향을 추적하기 어려움 -> 많은 "local influences"를 가지게 됨
- 어떤 $\hat{y}$은 주로 그 근처에 있는 $\hat{y}$들에 영향을 받게 됨. 후반에 있는 $\hat{y}$들은 초반의 $\hat{y}$의 영향을 받기 어려움. ("This is because whatever the output is, whether this got it right or wrong, it's just very difficult for the error to backpropagate all the way to the beginning of the sequence and therefore to modify how the neural network is doing computations earlier in the sequence")
- 이처럼 basic RNN의 단점은 vanishing gradient 문제가 발생할 수 있다는 거, 그리고 exploding gradients 문제도 발생할 수 있는데 이 경우 포착하기는 쉬움(numerical overflow 발생)
- exploding gradients 발생할 때: "gradients clipping" 적용해볼 수 있음 - gradient vector를 보았을 때 threshold보다 커지면 gradient vector를 너무 값이 커지지 않도록 re-scale
- 한편 vanishing gradients는 난이도가 높은 문제
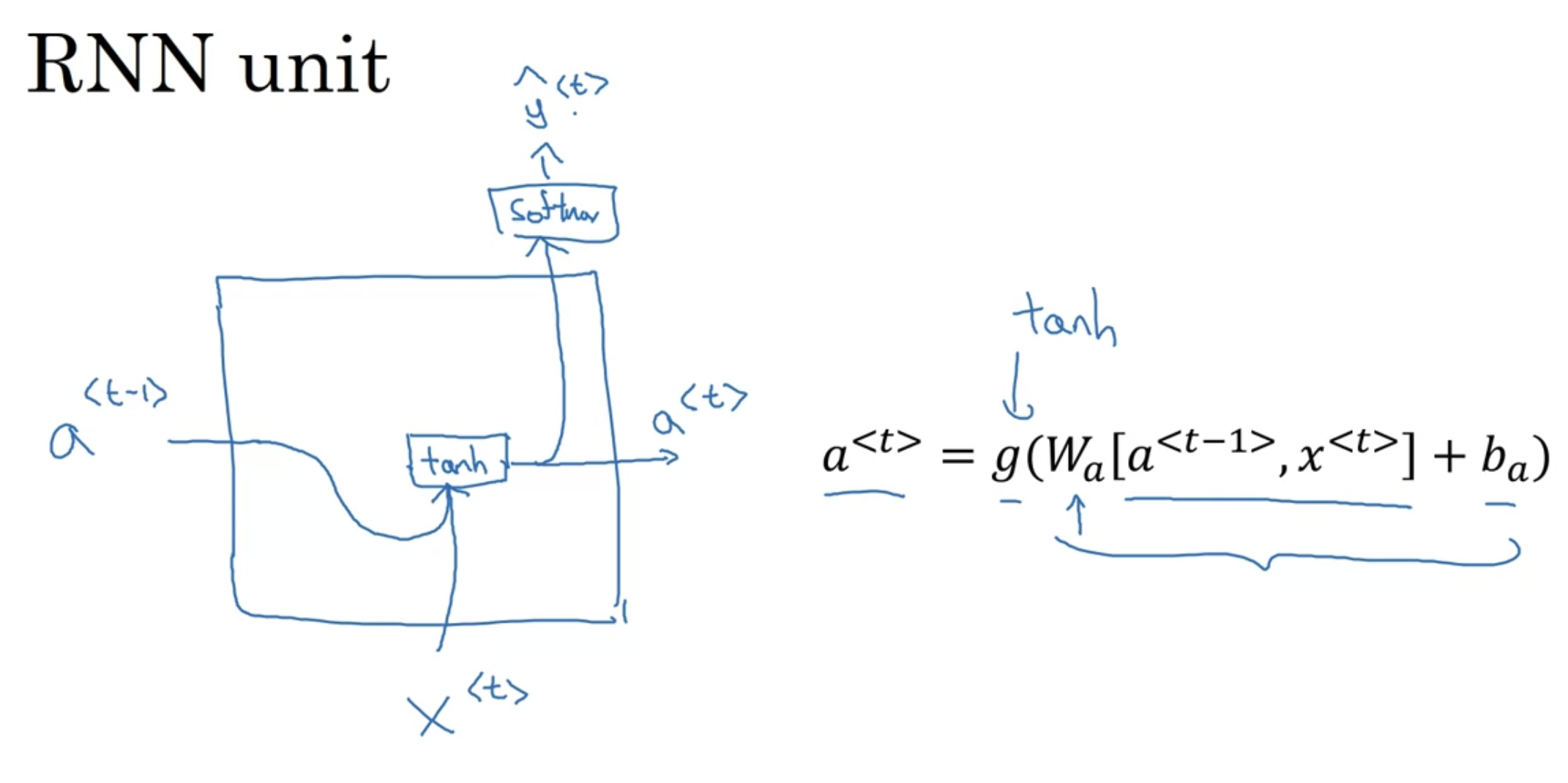
Gated Recurrent Unit(GRU)
$$a^{<t>} = g(W_{a}[a^{<t-1>}, x^{<t>}] + b_{a})$$
그림으로 나타냈을 때
[GRU]
"The cat, which already ate ..., was full"
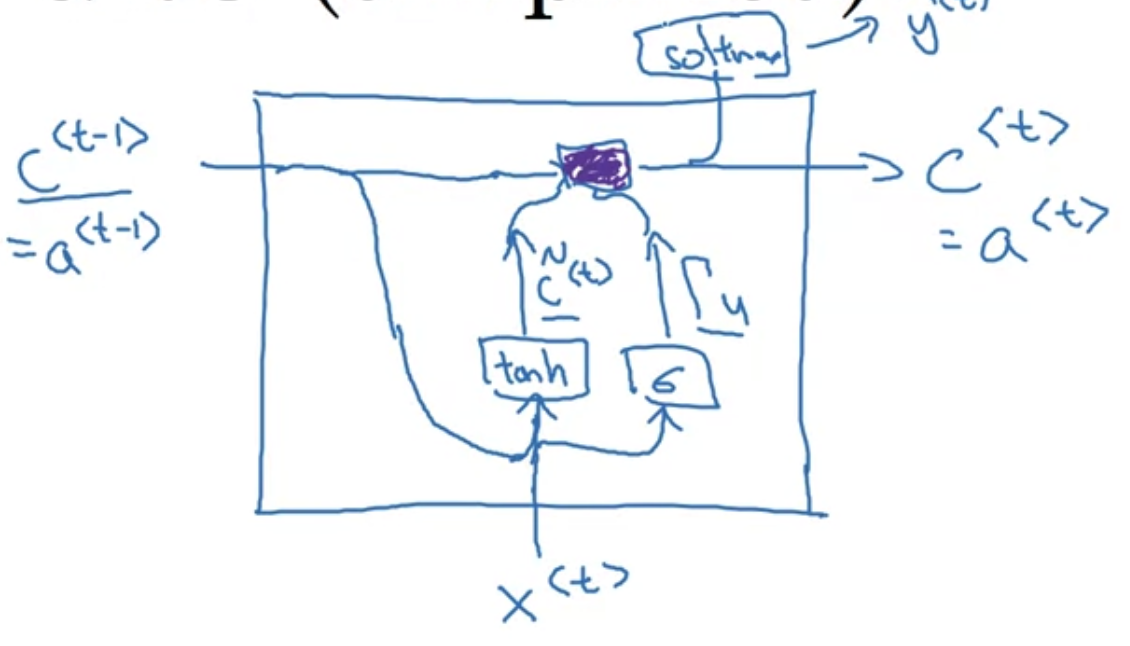
GRU에 나오는 새로운 변수 $c$, 즉 memory cell
$$c^{<t>} = a^{<t>}$$
좌항은 memory cell value, 우항은 output activation vlaue
(GRU에서는 같은 값을 다른 이름으로 부르는 것이지만, LSTM에서는 조금 다르므로 변수 $c$와 $a$를 구분해서 사용하기로 함)
$c^{<t>}$를 대체하기 위한 후보(?) 값 $\tilde{c}^{<t>}$ 설정
$$\tilde{c}^{<t>} = tanh (W_{c}[c^{<t-1>}, x^{<t>}] + b_{c})$$
$$\Gamma_{u} = \sigma (W_{u}[c^{<t-1>}, x^{<t>}] + b_{u})$$
- $u$는 'update gate' 뜻함
- $\Gamma_{u}$는 항상 거의 $0$ 아니면 $1$
- $c$를 이용해서 $\tilde{c}$를 업데이트한 후, 정말로 업데이트할 것인지 Gate를 통해서 판단
예를 들어,
"The cat, which already ate ..., was full"
위 문장에서 'cat'의 $c^{<t>}$를 $1$로 설정한다고 치자 (만약 'cats'였다면 $0$으로 설정)
GRU의 unit은 'was' 차례에 다다를 때까지 $c^{<t>}$값을 기억하고 있을 것
이때 $\Gamma_{u}$는 '언제 이 값을 업데이트할 건지' 결정함
$$c^{<t>} = \Gamma_{u} \ast \tilde{c}^{<t>} + (1- \Gamma_{u})\ast c^{<t-1>}$$
- 위 그림에서 보라색으로 칠한 것에 해당
- 만약 $\Gamma_{u}$가 1이면 $c^{<t>}$를 $\tilde{c}^{t}$로 대체, 0이면 원래 $c^{<t-1>}$로 설정
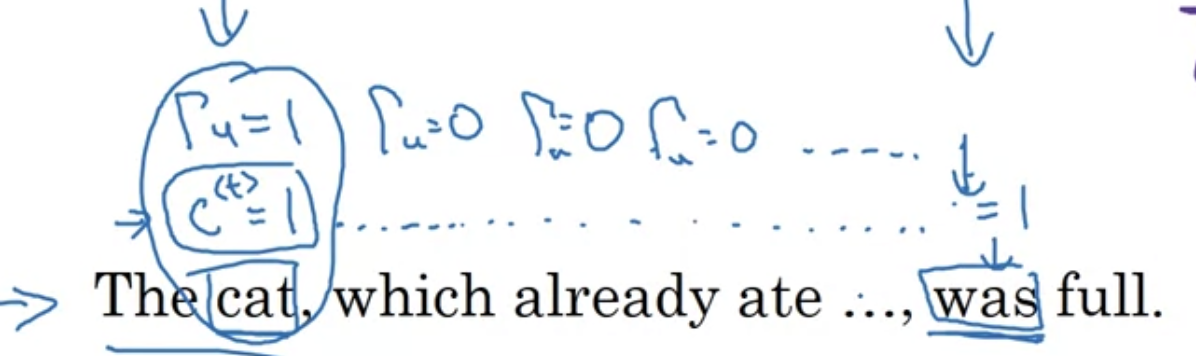
이러한 시스템이 좋은 점:
왼쪽부터 오른쪽으로 sequence를 스캔하면서 gate를 지남으로써 memory cell 을 업데이트 하기 좋은 타이밍이다 결정하고, 한참 전에 저장해둔 이 memory cell 값이 필요한 타이밍(위 예시에서는 "was")이 올 때까지 계속 바꾸지 않음

- gate $\Gamma_{u}$ 는 $0$으로 설정되기 쉽다
- $\Gamma_{u} = \sigma (W_{u}[c^{<t-1>}, x^{<t>}] + b_{u})$에서 $W_{u}[c^{t-1}, x^{t}] + b_{u}$의 값이 large negative value 인 이상 $\Gamma_{u}$ 는 본질적으로 $0$이다. ($0$에 매우 가까운 값이다)
- 이 경우 $c^{<t>} = c^{<t-1>}$ 이 됨; 그 셀을 위한 값을 유지하는 데 매우 유리
- $\Gamma_{u}$ 가 $0$에 매우 가까운 값이기 때문에 vanishing gradient problem을 다소 피할 수 있다
- $\Gamma_{u}$ 가 $0$에 너무 가까우면 본질적으로 $c^{<t>} = c^{<t-1>}$ 이기 때문에 여러 스텝을 지나도 $c^{<t>}$의 값이 유지됨
- gradient vanishing 문제에 유리하고, long-range dependencies도 잘 학습할 수 있게 됨
- hidden activation 값이 100차원이면 $c^{<t>}$도 100차원 벡터
- $\tilde{c}^{<t>}$도 동일한 차원의 벡터
- $\Gamma_{u}$도 동일한 차원의 벡터: which are the bits you want to update
--> $c^{t} = \Gamma_{u} \ast \tilde{c}^{t} + (1- \Gamma_{u})\ast c^{t-1}$ 에서 $\ast$는 element-wise multiplication
--> timestep 마다 어떤 차원에서 memory cell 벡터를 업데이트할지 알려줌
"You can choose to keep some bits constants while updating other bits." 예를 들어, bit 하나를 사용해서 고양이 단수/복수 여부를 기억하고, 또 다른 bit 몇 개를 써서 food에 대해 이야기하고 있음을 기억할 수 있음. 그러면 나중에 full이라는 것을 생각할 수 있음. 다양한 bit를 사용하고 이 bit들의 subset들만 바꿔가며 쓸 수 있음.
[Full GRU]
| $\tilde{c}^{<t>} = tanh (W_{c}[c^{<t-1>}, x^{<t>}] + b_{c})$ $\Gamma_{u} = \sigma (W_{u}[c^{<t-1>}, x^{<t>}] + b_{u})$ $c^{<t>} = \Gamma_{u} \ast \tilde{c}^{<t>} + (1- \Gamma_{u})\ast c^{<t-1>}$ |
-> 위에서 본 간소화된 버전과 비교할 것
$\tilde{c}^{<t>} = tanh (W_{c}[\Gamma_{r} \ast c^{<t-1>}, x^{<t>}] + b_{c})$
- $\Gamma_{r} \ast$ : $r$은 'relevance'를 뜻함. $c^{<t-1>}$이 얼마나 relevant한지 말해주는 역할.
- $\Gamma_{r}$ 는 어떻게 계산?
$\Gamma_{u} = \sigma (W_{u}[c^{<t-1>}, x^{<t>}] + b_{u})$
$\Gamma_{r} = \sigma (W_{r}[c^{<t-1>}, x^{<t>}] + b_{r})$
$c^{<t>} = \Gamma_{u} \ast \tilde{c}^{<t>} + (1- \Gamma_{u})\ast c^{<t-1>}$
- 논문에서 $\hat{c}^{<t>}$, $\Gamma_{u}$, $\Gamma_{r}$, $c^{<t>}$ 대신에 $\tilde{h}$, $u$, $r$, $h$ 를 쓴다는 점 유의
Long Short Term Memory(LSTM)

LSTM 식들은 아래와 같다
$$\tilde{c}^{<t>} = tanh(W_{c}[a^{<t-1>}, x^{<t>}]+b_{c})$$
$$\Gamma_{u} = \sigma(W_{u}[a^{<t-1>}, x^{<t>}]+b_{u})$$
$$\Gamma_{f} = \sigma(W_{f}[a^{<t-1>}, x^{<t>}]+b_{f})$$
$$\Gamma_{o} = \sigma(W_{o}[a^{<t-1>}, x^{<t>}]+b_{o})$$
$$c^{<t>} = \Gamma_{u} \ast \tilde{c}^{<t>} + \Gamma_{f} \ast c^{<t-1>}$$
$$a^{<t>} = \Gamma_{o} \ast tanh\ c^{<t>}$$
- $u$, $f$, $o$ : 각각 update gate, forget gate, output gate 의미
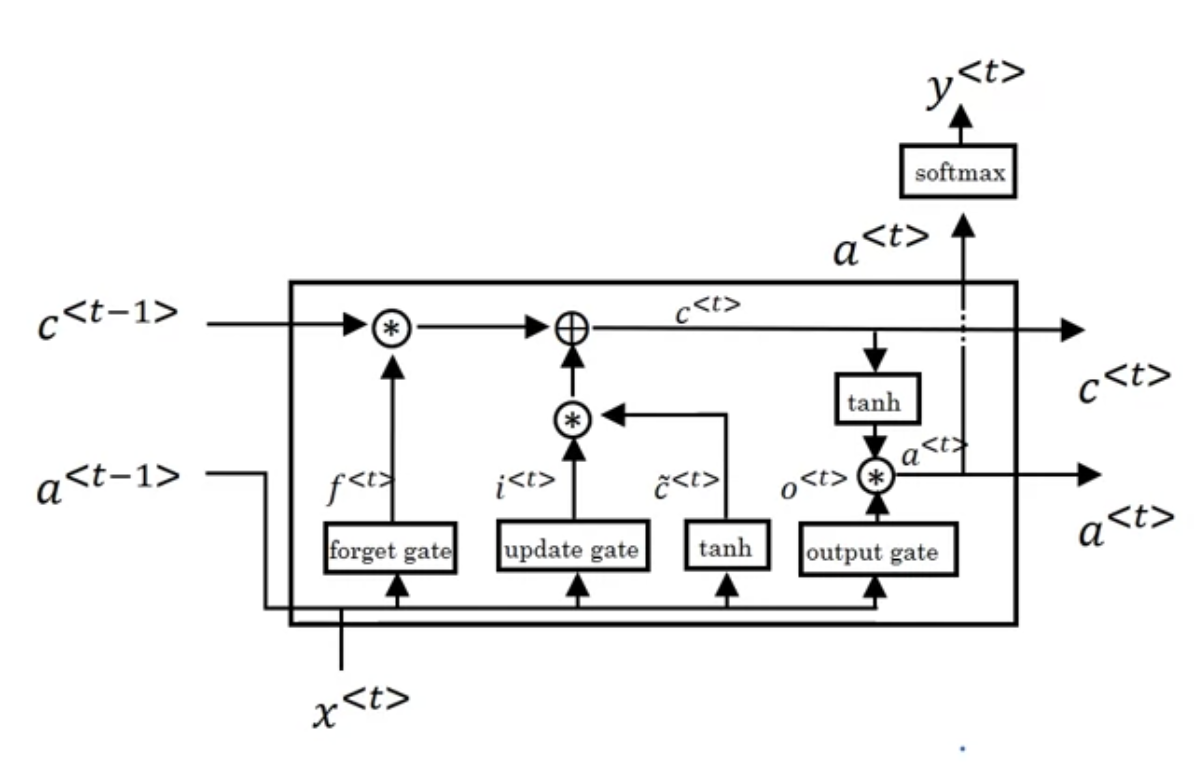
- $a^{<t-1>}$, $x^{<t>}$ 가 forget gate, update gate, output gate 로 들어가는 것 확인할 수 있음-
- 또한 tanh 활성화 함수로 들어가서 $\tilde{c}^{<t>}$ 출력함
- 복잡한 과정을 거쳐서 $c^{<t-1>}$ 는 $c^{<t>}$로 출력됨
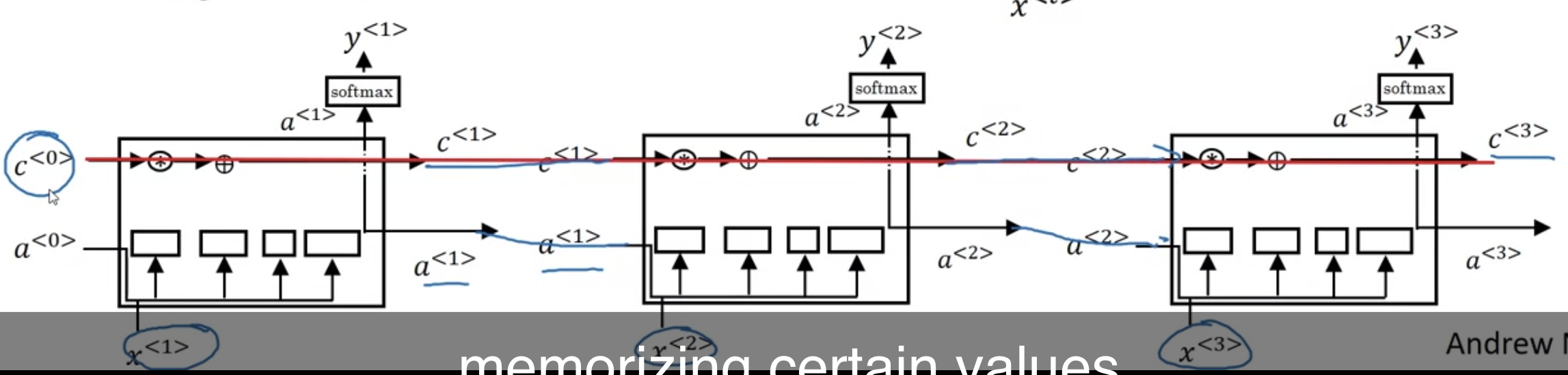
위 셀을 연결해 이어 붙이면 $c$값이 연결되어 있는 것을 볼 수 있음
- gate값 계산할 때 $a^{<t-1>}$, $x^{<t>}$ 뿐만 아니라 $c^{<t-1>}$를 넣는 variation도 있다 --> "peephole connection"
- gate값들이 100차원 벡터라고 쳤을 때 (100차원의 hidden memory cell unit 을 가지고 있을 때), $c^{<t-1>}$의 다섯번째 요소가 상응하는 게이트들의 5번째 요소에만 영향을 준다면 그 관계는 one-to-one 으로, 100차원의 $c^{<t-1>}$의 모든 요소가 gate들의 모든 요소에 영향을 주는 것이 아니라, $c^{<t-1>}$의 첫번째 요소가 게이트들의 첫번째 요소에 영향을 주고 두번째 요소가 두번째 요소에 영향을 주고 .. and so on.
- GRU가 조금더 가벼운 느낌? 큰 모델 만들기에 좋다
- 굳이 골라야 한다면 LSTM 을 디폴트로 먼저 써보는 게 국룰인데 GRU 쓰는 게 더 편할 수도 있다
Bidirectional RNN
[Getting information from the future]
- He said, "Teddy bears are on sale!"
- He said, "Teddy Roosevelt was a great President!"
-> 위 두 문장을 가지고 name entity recognition을 해본다고 하자
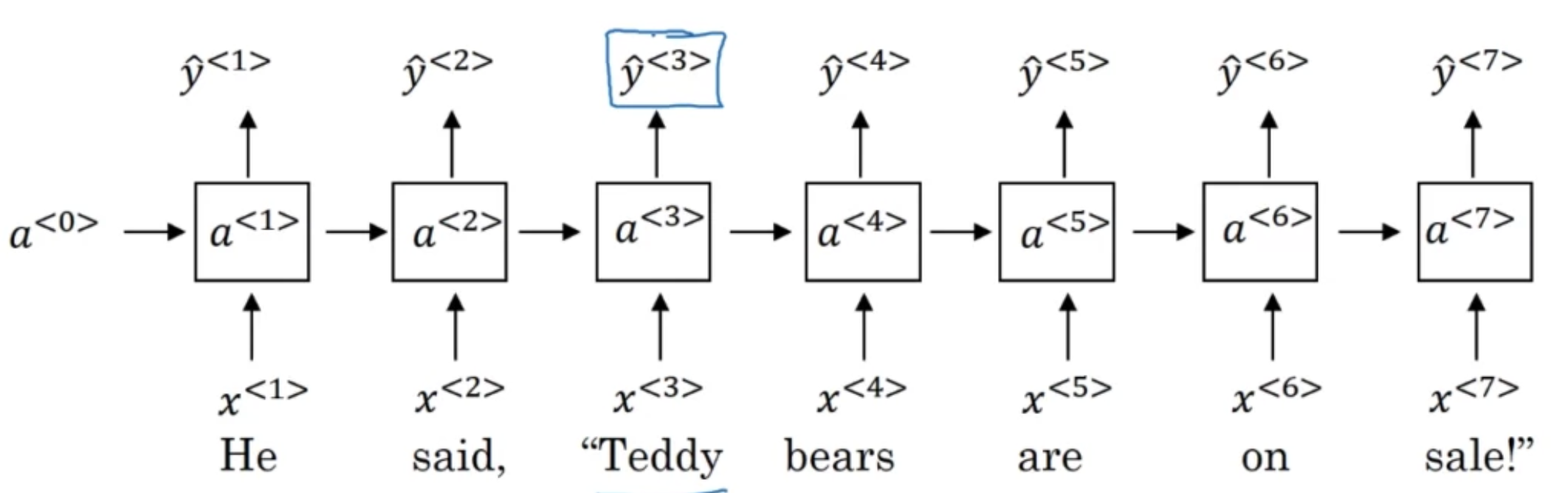
$\hat{y}^{<3>}$은 0을 출력해야 할까, 1을 출력해야 할까?
[Bidirectional RNN(BRNN)]
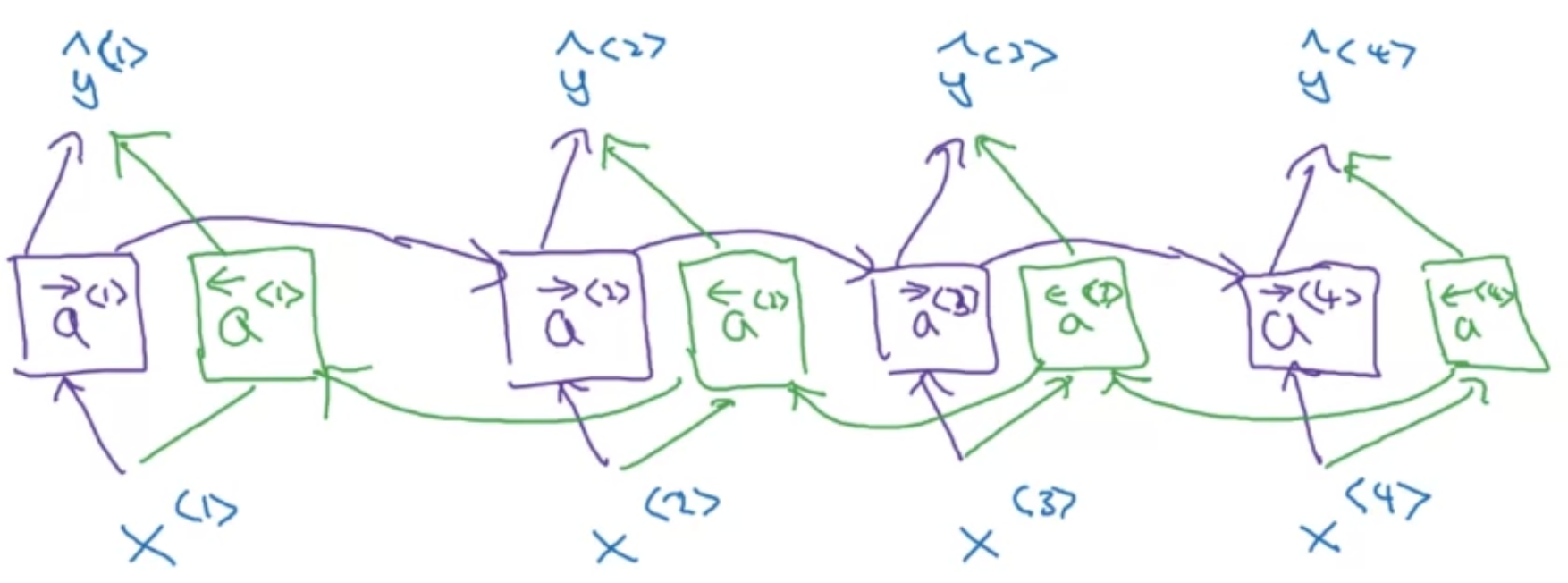
- 보라색 : uni-directional RNN ($\overrightarrow{a}$는 forward 의미)
- 초록색 : bi-driectional RNN을 위한 추가 유닛 ($\overleftarrow{a}$는 backward 의미)
- Acyclic graph
- 과거, 현재, 미래의 정보를 활용한다
- $\overleftarrow{a}$는 오른쪽에서 왼쪽 방향으로 구하는 활성화값 (back prop 아님)
- GRU, LSTM 블록으로 대체해도 괜찮음
- NLP 문제 해결할 때 LSTM 블록으로 구성된 bi-directional RNN 자주 씀
$$\hat{y}^{<t>} = g(W_{y}[\overrightarrow{a}^{<t>}, \overleftarrow{a}^{<t>}]+b_{y})$$
- 단점 : 어느 곳에서든 예측하려 한다면 전체 데이터 시퀀스가 필요함(ex. speech recognition 이라면 사람의 말이 끝날 때까지 기다렸다가 예측해야 함)
Deep RNNs
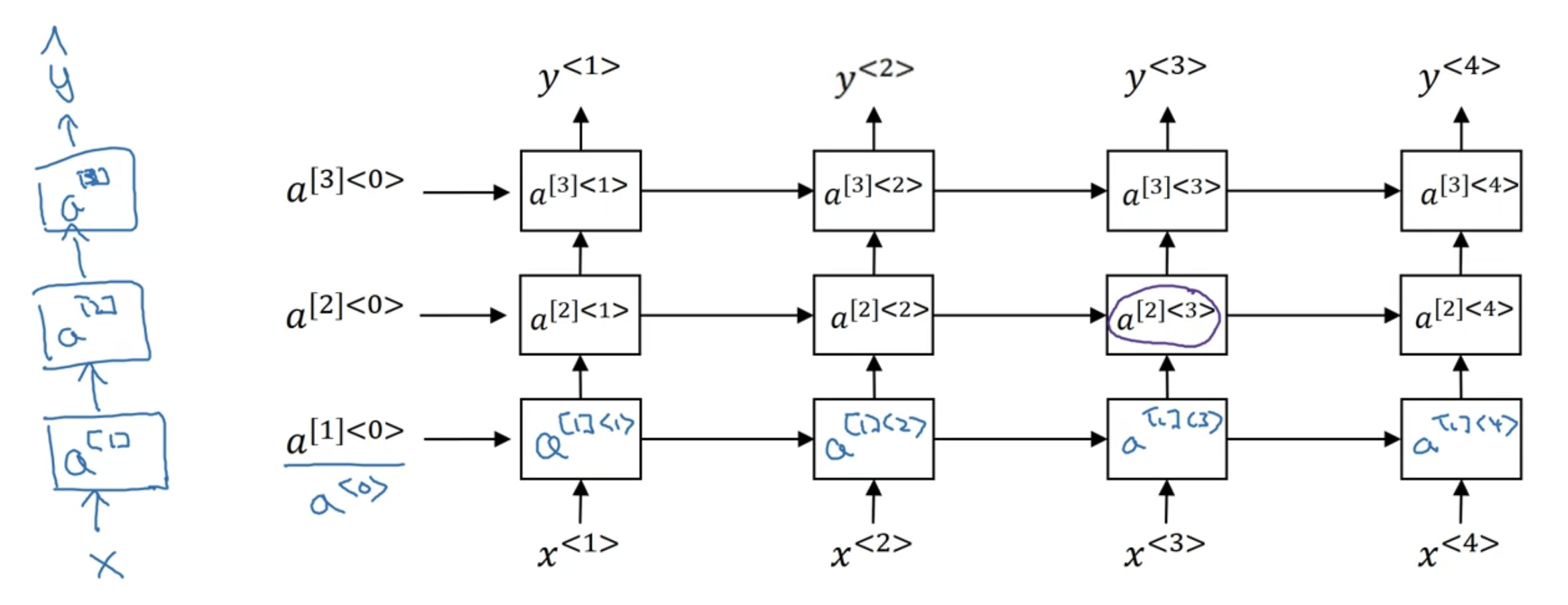
- 맨 왼쪽의 일반적인 NN 구조에 착안하여, 레이어별로 시간 차원으로 RNN 블록들을 쌓는다고 생각
- $a^{[l]<t>}$ : $l$번째 레이어의 $t$번째 time step
예를 들어 $a^{[2]<3>}$값을 구한다고 치면, (입력되는 화살표에 주목)
$$a^{[2]<3>} = g(W_{a}^{[2]} [a^{[2]<2>}, a^{[1]<2>}]+b_{a}^{[2]})$$
- $W_{a}^{[2]}$, $b_{a}^{[2]}$는 $2$번째 레이어에서 공유되는 파라미터들
- 시간 차원까지 더해져 이미 unit 개수가 매우 많으므로 100레이어까지 깊게 만들지는 않음
- RNN 블록 이후에 NN unit으로 더 연결하기도 함(세로로 더 추가) -> 이 경우 가로로는 더이상 연결되지 않음
- GRU, LSTM 블록으로 만들어도 됨
'인공지능 > DLS' 카테고리의 다른 글
| [5.2.] Learning Word Embeddings: Word2vec & GloVe (0) | 2022.08.09 |
|---|---|
| [5.2.] Introduction to Word Embeddings (0) | 2022.08.07 |
| [5.1.] Recurrent Neural Networks(2) (0) | 2022.08.02 |
| [5.1.] Recurrent Neural Networks(1) (0) | 2022.08.02 |
| [4.4.] Neural Style Transfer (0) | 2022.08.02 |