최소 신장 트리 찾기 문제를 풀어보려고 했더니, 크루스칼 알고리즘을 알아야 된다고 한다.
크루스칼 알고리즘을 공부하려고 했더니, 합집합 찾기 알고리즘을 알아야 한다고 한다.
오늘은 합집합 찾기 union find 알고리즘을 공부해보자!
1. 크루스칼(Kruskal) 알고리즘
- 가장 적은 비용으로 모든 노드를 연결한다
- 그리디 알고리즘에 해당한다
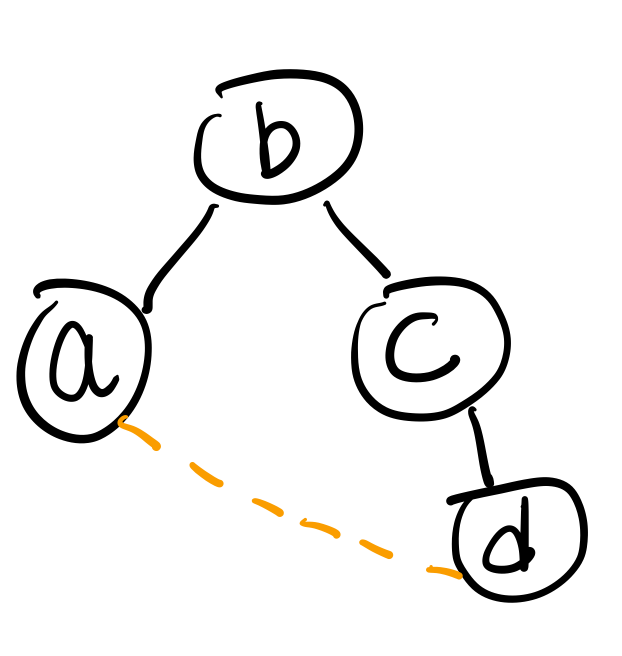
- 최소 신장 트리에는 사이클이 존재하면 안 되는데, 사이클의 발생 여부를 union-find로 확인할 수 있다

- 노드 a 와 노드 d 가 이미 같은 그래프에 속하는데, 두 노드를 연결한다면 사이클이 발생한다!!
- 따라서 두 노드가 같은 그래프에 속하는지 확인하기 위해 union-find 알고리즘을 사용한다
2. 합집합 찾기(union find)
- 서로소 집합 혹은 분리 집합(disjoint set)을 표현한다
- 서로소 집합 : 공통 원소가 없는 두 집합, 상호배타적인(동시에 일어날 수 없음) 부분집합들
- 서로소 집합을 표현하기 위해서는 아래의 두 연산이 필요하다
(1) union : 각 원소가 속한 두 집합을 하나로 합친다
(2) find : 특정 원소가 어떤 집합에 속하는지 찾는다
하지만 집합을 어떻게 표현해야 어떤 원소들이 같은 집합에 속하는지 판단할 수 있을까?
-> 하나의 원소에 대해, 그 원소가 속한 집합의 대푯값인 root를 저장한다.
-> find : 특정 원소가 속한 집합의 root를 반환한다

위에 두 개의 그래프가 있다
"원소2 와 원소4 가 같은 그래프(집합)에 속할까?"에 대답하려면 어떻게 해야 할까?
간단하게 엣지를 타고 이동해서 확인한다고 해보자. 원소2 -> 원소1 -> 원소3 -> 원소4 로 이동할 수 있는지 확인할 수 있다.
하지만 원소2와 원소4 사이에 2,147,483,647개의 노드가 존재한다면 이 방법은 매우 비효율적이다.
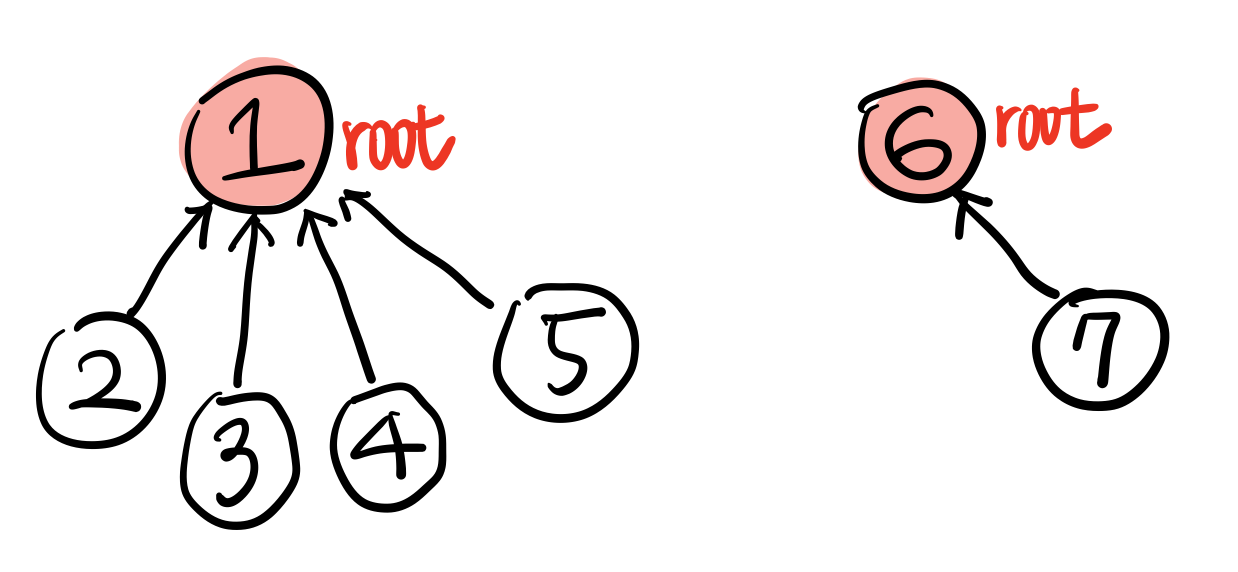
그래서 각 그래프의 대푯값인 root를 지정하고, 같은 root를 공유하는지 확인하기로 한다. root가 다르면 다른 그래프인 것이다.
(통상적으로 root는 값이 작은 노드로 지정한다)
위에서 원소2와 원소4는 root가 둘다 1이기 때문에 같은 그래프(집합)에 속한다고 볼 수 있다
3. union find의 동작 과정
(영 헷갈려서 예제를 두 개 가져와봤다)
3.1. 예제1 : 왜 find를 하는 걸까?
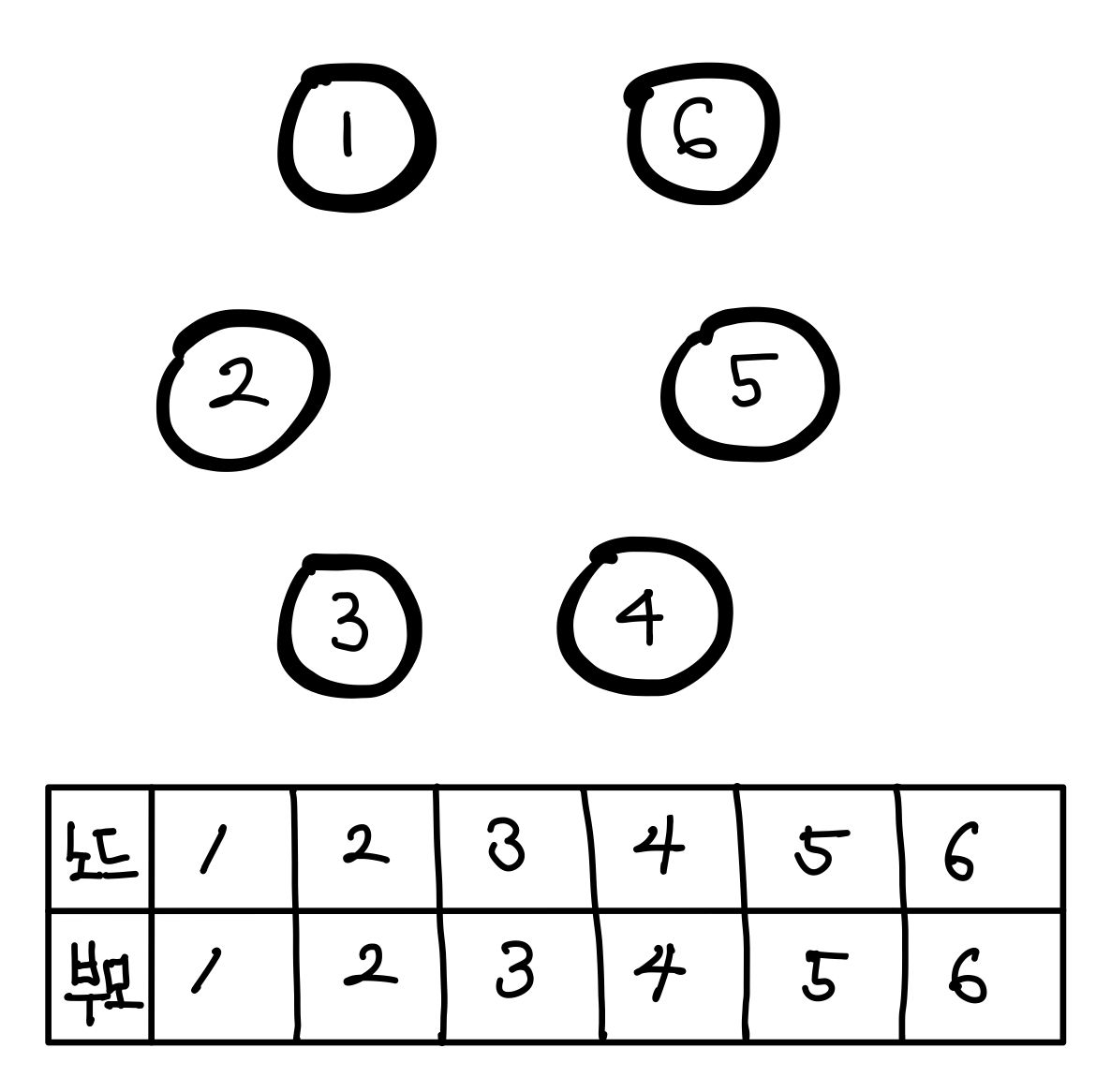
노드끼리 전혀 연결되어 있지 않은 상태의 그래프를 보자. 각 노드의 부모는 자기 자신이다.
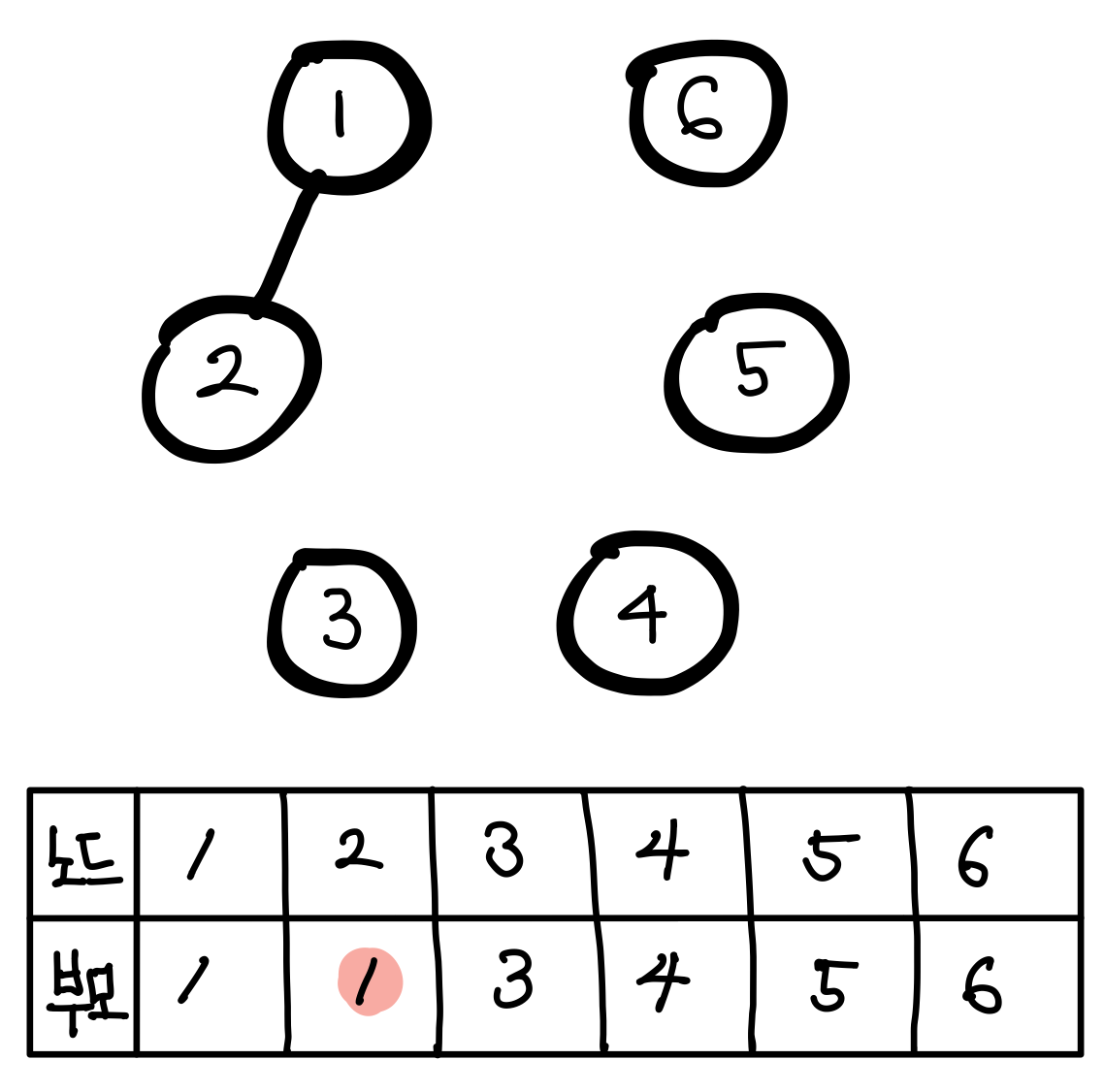
노드 1과 노드2 를 연결해보았다. 즉, 두 원소가 속하는 두 집합을 하나의 집합으로 합쳤다(union). 노드2의 부모는 1로 변경되었다.
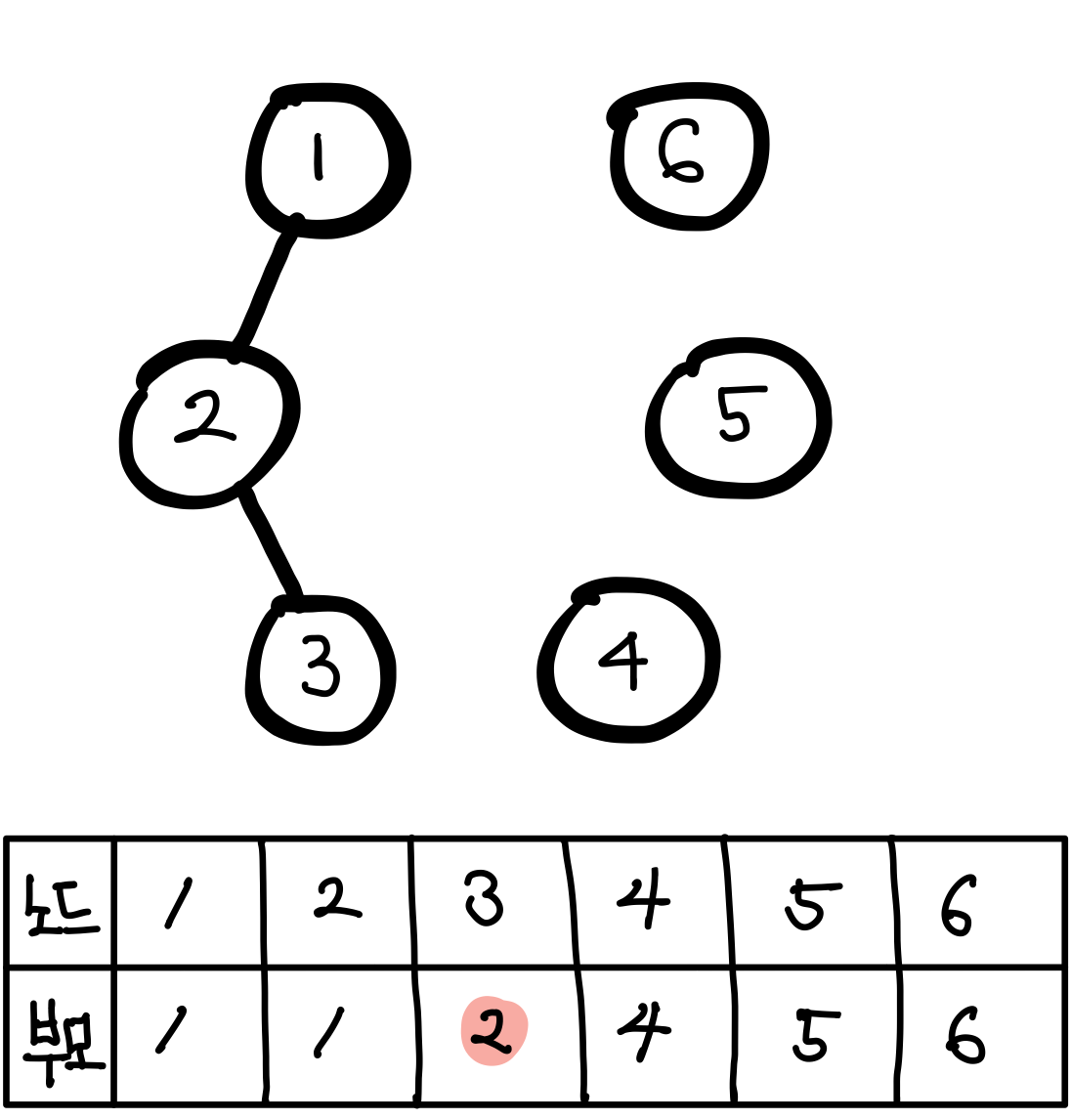
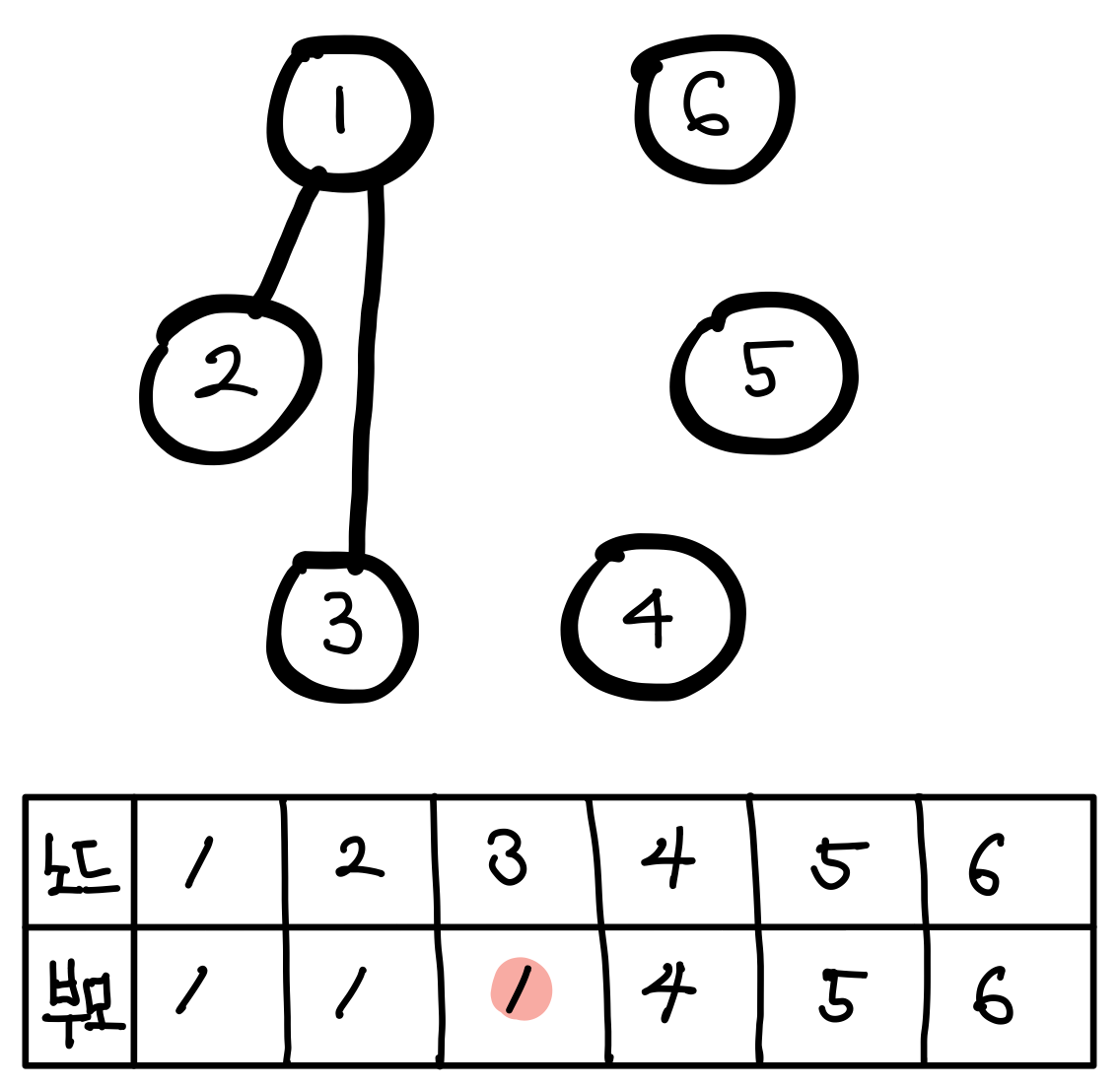
원소2와 원소3을 union 하여 같은 집합으로 만든다. 원소3의 부모는 2가 된다. (왼쪽 이미지)
원소3의 부모가 1이 될 경우 오른쪽 그림과 같이 다른 그래프를 나타낸다.
원소2와 원소3의 부모가 다른데, 같은 그래프인지 어떻게 알 수 있을까? 그래서 이때 find 연산을 한다.
내 부모 원소의 부모 원소를 찾아가다 보면 그 집합의 root가 나오겠지.
예를 들어 원소3의 부모가 원소2이니까, 원소2의 부모인 원소1까지 find 하며 올라간다. 그 집합을 대표하는 root인 원소1이 나온다.
3.2. 예제2 : 어떻게 find 하는 걸까?
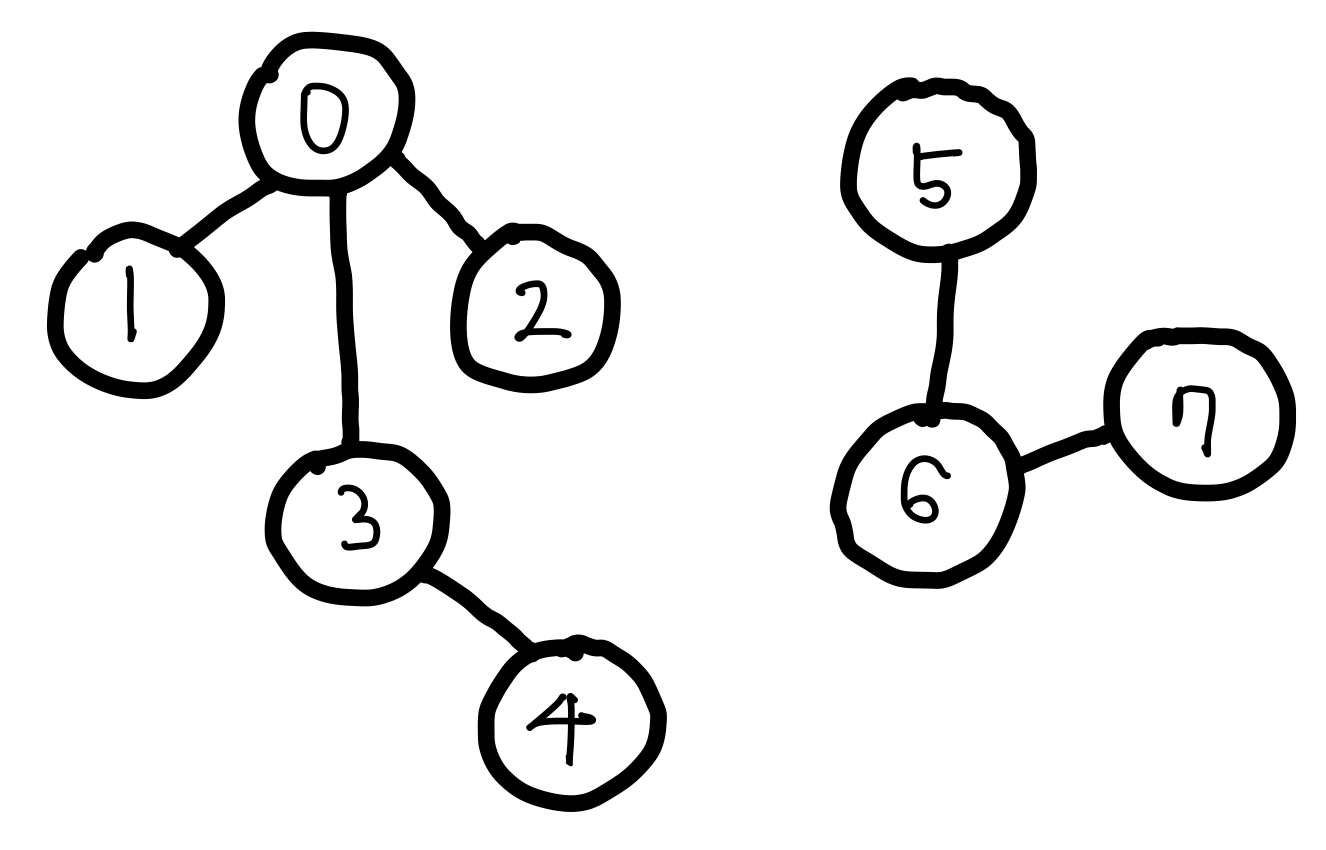
여기 서로 다른 두 개의 그래프가 있다
처음에는 아래와 같이 자기 자신으로 초기화한다
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
먼저 노드 0 을 부모로 삼는 것들을 바꿔본다
노드1, 노드2, 노드3이 노드0과 바로 연결되어 있으므로 표에서 0으로 바꿀 수 있다
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 4 | 5 | 6 | 7 |
그리고 노드4의 부모는 노드 3이다
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 3 | 5 | 6 | 7 |
그런데 노드4의 부모인 노드3 말이다. 노드3의 부모가 0이다.
그리고 노드0의 부모는 자기 자신인 노드0이다. 따라서 표를 아래와 같이 수정할 수 있다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 0 | 5 | 6 | 7 |
즉, 자기 자신을 부모로 가지는 노드가 나올 때까지 부모 노드를 갱신하는 것이다.
오른쪽 그래프에 대해서도 같은 방식을 적용하면 된다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 0 | 5 | 5 | 5 |
(어떻게 union 하는 걸까? 는 아래의 기본 파이썬 코드를 통해 확인해보겠다)
4. 파이썬 코드
4.1. 기본
parents = [i for i in range(MAX_SIZE)]
# 재귀 함수
def find(parent, x):
# 루트 노드의 부모 노드 번호는 자기 자신이다.
if parent[x] == x:
return x
# 각 노드의 부모 노드를 찾아 올라간다.
else:
return find(parent, parent[x])
def union(parent, x, y):
# 각 원소가 속한 트리의 루트 노드를 찾는다.
rootX = find(parent, x)
rootY = find(parent, y)
parent[rootY] = rootX
find 연산과 union 연산을 정의했다
1) parents (위에서 표로 나타낸 것) 리스트를 자기 자신으로 채워 초기화한다
2) 재귀함수로써 find 연산을 구현 : 주어진 노드의 부모 노드가 자기 자신이면 반환, 그렇지 않으면 부모 노드를 넘겨주며 재귀
(부모의 부모의 부모의 ... 자기자신이 나올 때까지 찾아간다)
3) find 함수를 활용하여 union 연산을 구현 : 원소 x, y의 각 root 를 반환, 한쪽 root를 다른쪽 root를 부모로 삼음으로써 하나의 집합으로 합친다
(ex. 위 그래프에서 원소2의 root가 원소0이고, 원소6의 root가 원소 5인데, 자기 자신이 부모였던 원소0에게 원소5를 부모로 삼게 만드는 것이다. 대표자가 다른 대표자한테 굴복함.)
4.2. 최적화
작은 트리를 큰 트리에 붙이는 식으로 union한다 (균형 있는 트리가 생성됨)
지금까지 단순하게 그래프를 기준으로 설명해왔는데, 계층을 가지는 트리로 생각해볼 수 있다
각 노드는 자기 자신을 루트로 삼는 서브 트리의 높이를 rank로 저장한다
쉽게 트리의 높이를 rank라고 생각해도 될 것 같다 (잘못된 정보라면 알려주세요)
find 함수
parents = [i for i in range(MAX_SIZE)]
def find(parent, x):
if parent[x] == x:
return x
# 경로 압축(Path Compression)
# find 하면서 만나는 모든 값의 부모 노드를 root로 만듦.
parent[x] = find(parent, parent[x])
return parent[x]*이거 위의 find 함수랑 뭐가 다른지 모르겠어요...
union 함수
parents = [i for i in range(MAX_SIZE)]
rank = [0 for _ in range(MAX_SIZE)]
# find()는 위와 동일
def union(parent, x, y, rank):
rootX = find(parent, x)
rootY = find(parent, y)
# 두 값의 root가 같으면(이미 같은 트리) 연결 X(합치지 않음)
if rootX == rootY:
return
# union-by-rank 최적화
# 항상 높이가 더 낮은 트리를 높이가 높은 트리 밑에 넣음.
# --> 높이가 더 높은 쪽을 root로 함.
if rank[rootX] < rank[rootY]:
parent[rootX] = rootY
else:
parent[rootY] = rootX
if rank[rootX] == rank[rootY]:
rank[rootX] += 1 # 만약 높이가 같다면 합친 후 -> x 높이 + 1
rank를 비교해서 낮은 쪽을 큰 쪽에 붙인다.
만약 두 트리의 rank가 동일하다면, 합쳐진 rank는 기존 rank에 +1 한 값이 된다
참고
- https://velog.io/@kimdukbae/Union-Find-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
- https://velog.io/@aszxvcb/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%A7%91%ED%95%A9
'컴퓨터 > 알고리즘&자료구조' 카테고리의 다른 글
| 최소 신장 트리 구하기 : 프림(Prim's) 알고리즘 (0) | 2022.10.05 |
|---|---|
| 최소 신장 트리 구하기 : 크루스칼(Kruskal) 알고리즘 (0) | 2022.10.05 |
| 자료구조 : 힙(heap) (0) | 2022.09.27 |
| 최단 경로 문제: 다익스트라 알고리즘 (0) | 2022.09.26 |
| 최단 경로 문제: 벨만포드 알고리즘 (1) | 2022.09.26 |