1. 최단 경로 문제란?
- 정점 u에서 정점 v까지의 경로 중에서 경로의 값이 가장 작은 경로를 찾는다
- δ(u,v)
2. 벨만포드 알고리즘
2.1. 음수 간선의 값(negative-weight edges)

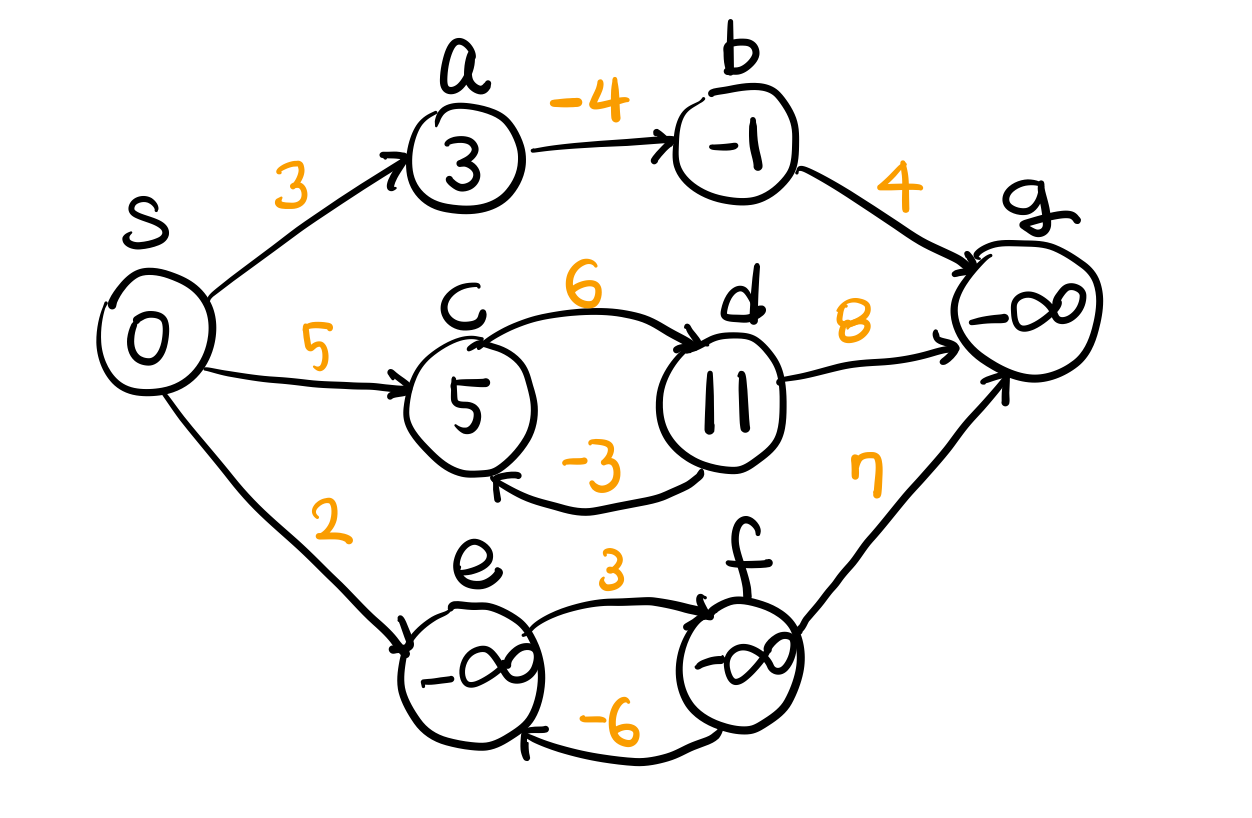
이렇게 생긴 경로 그래프가 있고, s 에서 g로 가는 경로를 구하려고 한다.
총 세 가지 경로를 생각해볼 수 있는데, (1) ab 를 거쳐가는 경로 (2) cd 를 거쳐 가는 경로 (3) ef 를 거쳐 가는 경로다.
(1) ab 를 거쳐가는 경로

길이 하나 뿐이므로 경로의 값을 모두 더해서 구하면 된다 -> 3
(2) cd 를 거쳐 가는 경로

c 와 d 사이가 싸이클 형식으로 되어 있으므로 cd 안에서 싸이클을 돌고 이동할 수 있다
단 이 경로의 경우 싸이클을 돌수록 경로값이 +3 되므로 최단 거리를 구하는 우리 문제에서는 고려할 필요가 없다
(2) ef 를 거쳐 가는 경로

반면에 이 마지막 경로 같은 경우는 싸이클을 돌수록 경로값이 −3 된다
최단 경로를 구하려다가 이 무한대의 음수 싸이클에 빠질 수가 있기 때문에, 이런 경우를 피해야 한다
--> 음수 간선 자체가 문제가 되는 게 아니라, 시작점에도 도착점에 이르기까지 도달할 수 있는 음수 순환이 문제되는 것 ("가다가 만날 수 있는")
--> 최단 경로 = 출발점으로부터 도달가능하며 음의 값을 가지는 순환이 없는 경우
2.2. 직전 정점 하위 그래프
직전 정점 하위 그래프(predecessor subgraph) 중에서 가장 올바른 값(최적해 구조 optimal substructure)을 찾는 방법은?
- 완화(relaxation) : 현재 경로값보다 더 적은 경로가 존재하면 값을 변경한다
2.3. 벨만포드 알고리즘
- 하나의 시작점에서 하나의 도착점으로 가는 최단 경로 문제를 해결
- 음의 간선이 있는 경우에도 문제를 해결
- vertex를 기준으로 relax하는 다익스트라와는 다르게, 간선을 기준으로 relax한다는 특징이 있음
<pseudo code>
1. graph, weight, start 가 주어진다
2. (vertex-1)번 반복한다: graph 내 모든 edge에 대해서, relaxation 수행
3. 기존의 vertex 값과, 기존 vertex 값에 새로운 경로값을 더한 결과 중에서 무엇이 더 큰지 비교한다
(새로운 경로를 추가했을 때 기존 경로값보다 작아지는지 커지는지 비교하는 과정)
예제
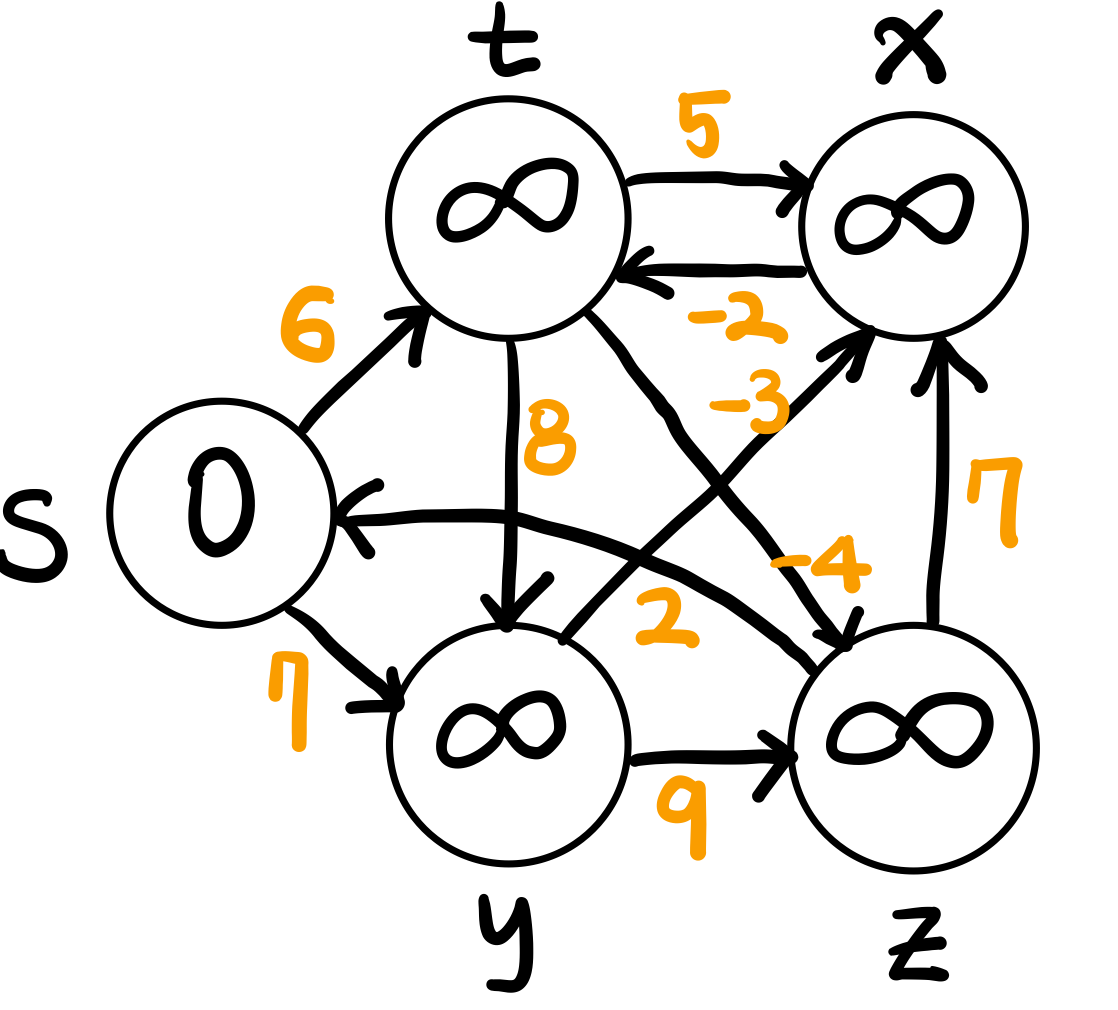
s(start)에서 각 vertex 로 가는 경로
- 처음에는 INF ∞ 로 초기화
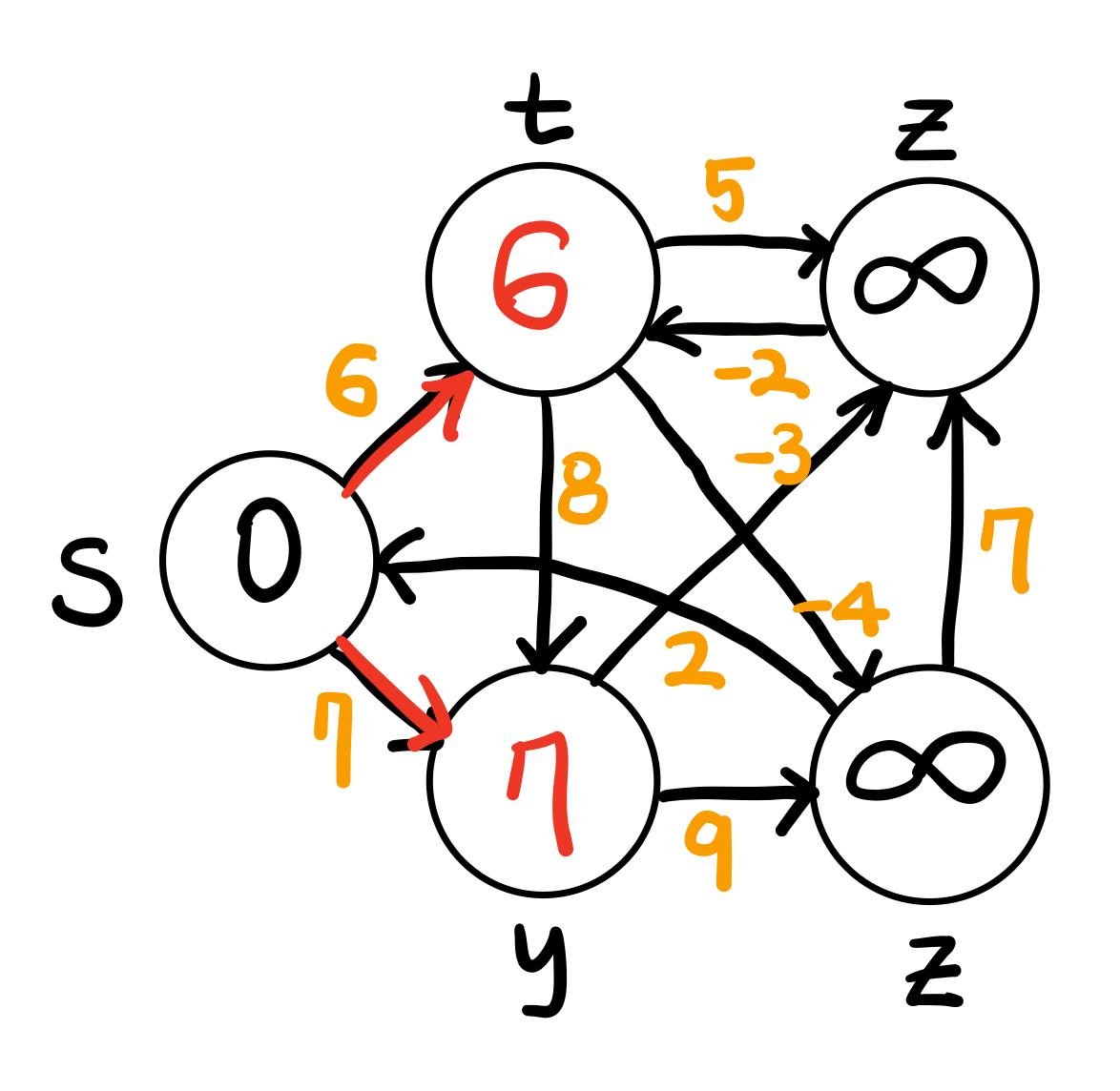
처음 s에서 t와 y로 가는 경로값은 각각 6, 7로 설정할 수 있다
그 다음, t와 y를 기준으로 relaxation을 반복한다

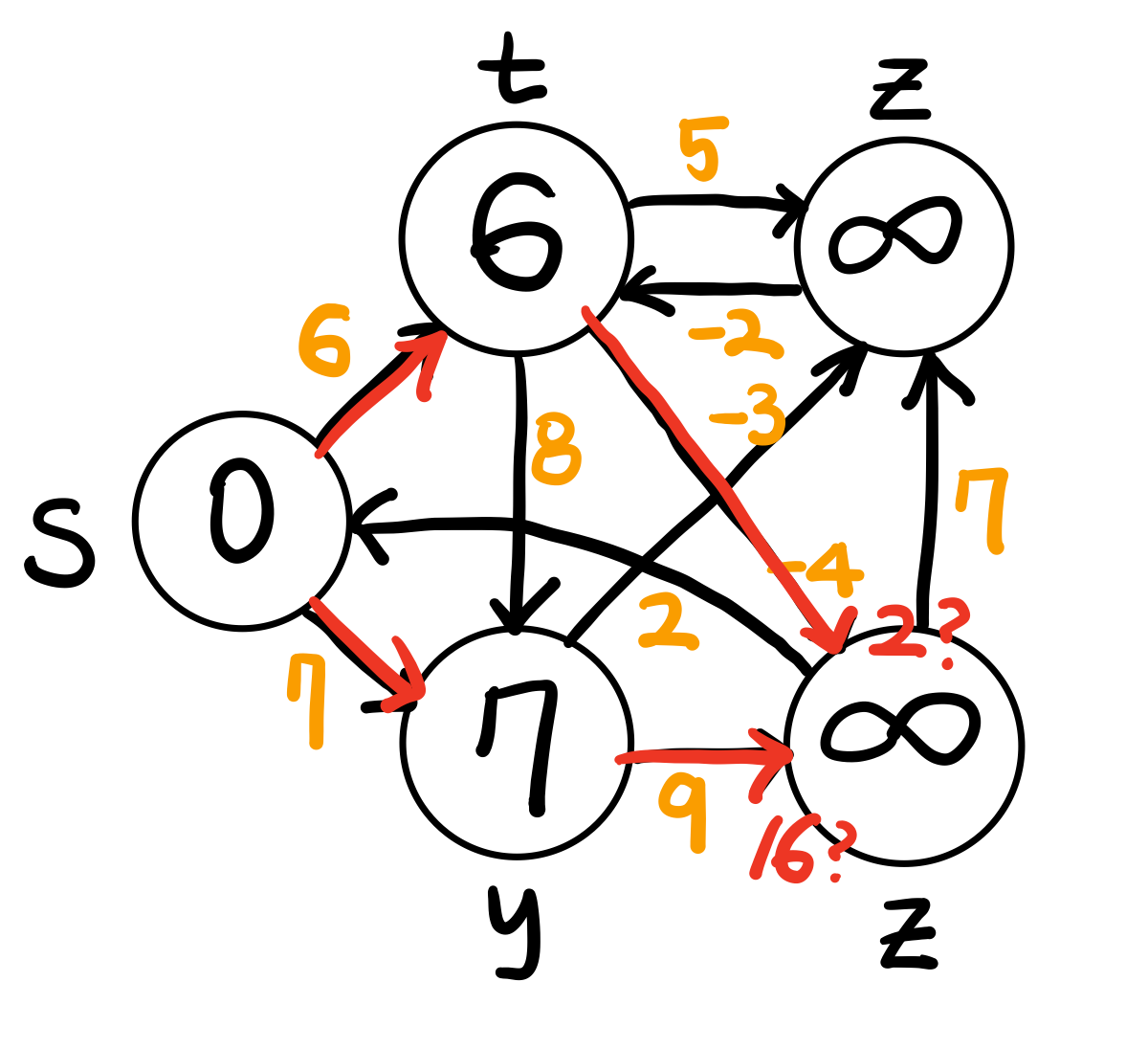
(왼) t와 y에서 x로 갈 때 비교, (오) t와 y에서 z로 갈 때 비교
**지금 쓰다가 알았는데 위쪽 z는 x를 잘못 쓴 겁니다!!!!!!!!
비교한 결과 아래와 같이 업데이트할 수 있다
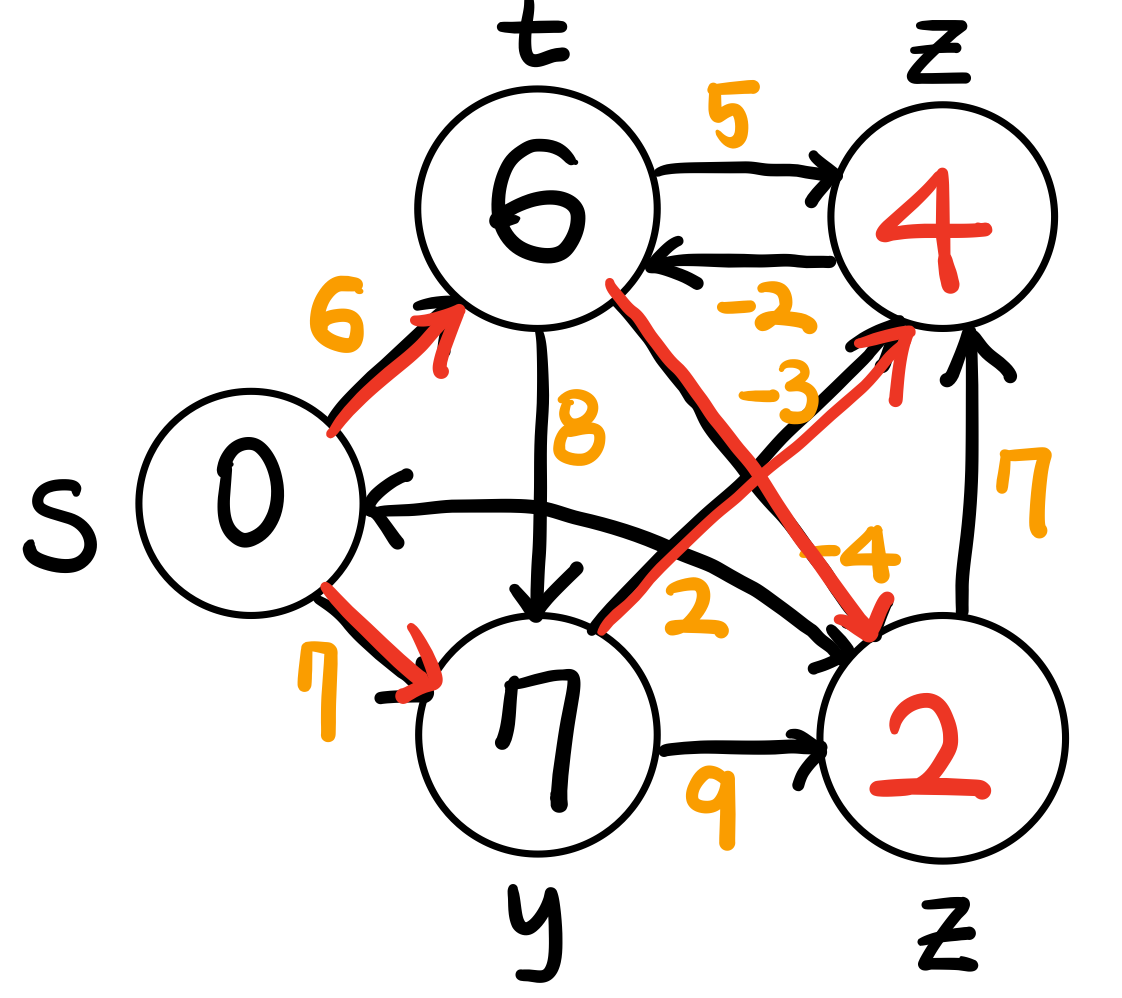
그 다음, x와 z를 기준으로 relaxation을 반복한다

x에서 t로 갈 수 있으며, 이때 경로값은 4+(−2)이기 때문에 t까지의 경로값을 2로 수정할 수 있음
z에서 s로 돌아가는 것은 의미 없으므로 패스
z에서 x로 갈 수 있으나, 경로값이 2+9로 더 커지므로 패스
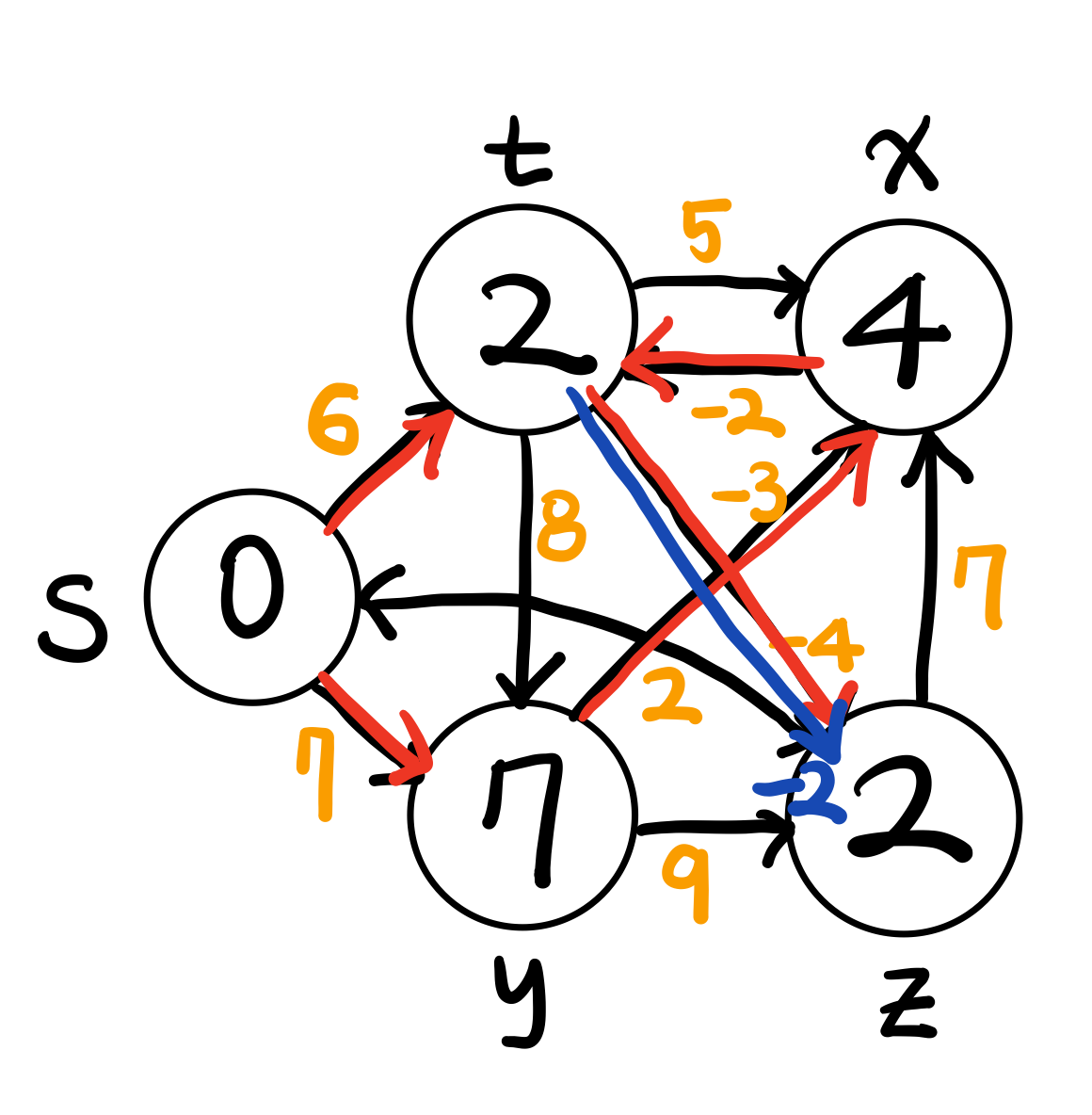
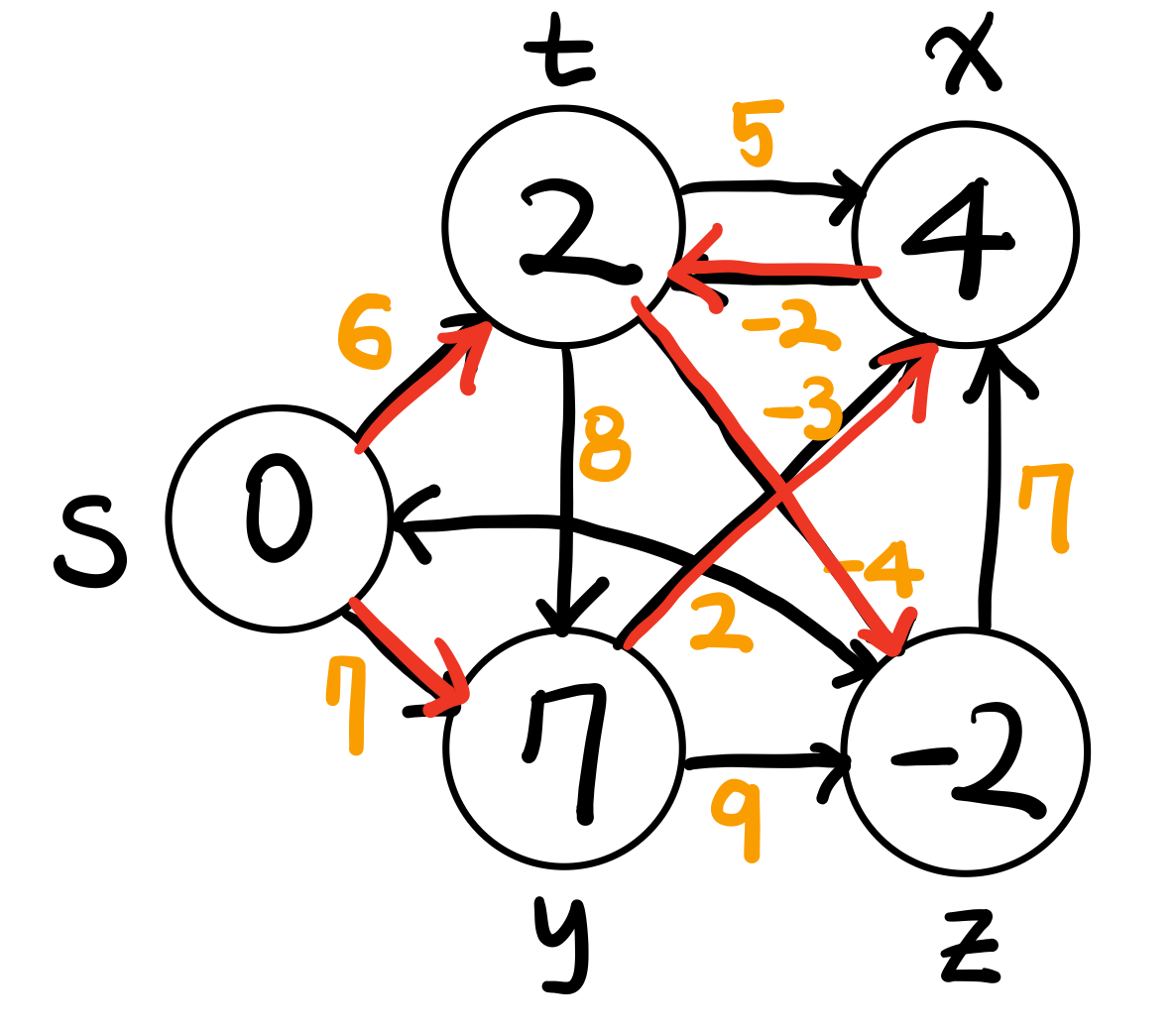
노드 t가 경로에 추가되었으므로 t에서 relaxation 또 수행, z로 갈 때 경로값이 −2로 작아지므로 업데이트할 수 있음
2.4. 수행시간
Vertex가 추가될 때마다 모든 edge를 추가하기 때문에 수행 시간은 O(VE)
3. 파이썬 코드
(업데이트 예정)
'컴퓨터 > 알고리즘&자료구조' 카테고리의 다른 글
| 최소 신장 트리 구하기 : 크루스칼(Kruskal) 알고리즘 (0) | 2022.10.05 |
|---|---|
| 합집합 찾기(union-find) (0) | 2022.10.05 |
| 자료구조 : 힙(heap) (0) | 2022.09.27 |
| 최단 경로 문제: 다익스트라 알고리즘 (0) | 2022.09.26 |
| 빅오표기법(Big-O notation)과 시간복잡도 (0) | 2022.09.25 |