1. 최단 경로 문제란?
벨만포드 알고리즘을 다룬 여기 문서 참고
2. 다익스트라 알고리즘
- 하나의 시작점에서 도착점으로 가는 최단 경로를 찾는 알고리즘
- 간선이 음의 값을 가져선 안 된다
<pseudo code>
1. graph, weight, start 가 주어진다
2. start(자기 자신)까지의 거리는 0으로 상정한다
3. 모든 vertex 들을 queue에 넣고 반복한다
- queue에 들어간 v 중에서 가장 작은 값을 찾아 뽑는다
- 뽑힌 v에 대해서 relaxation 수행
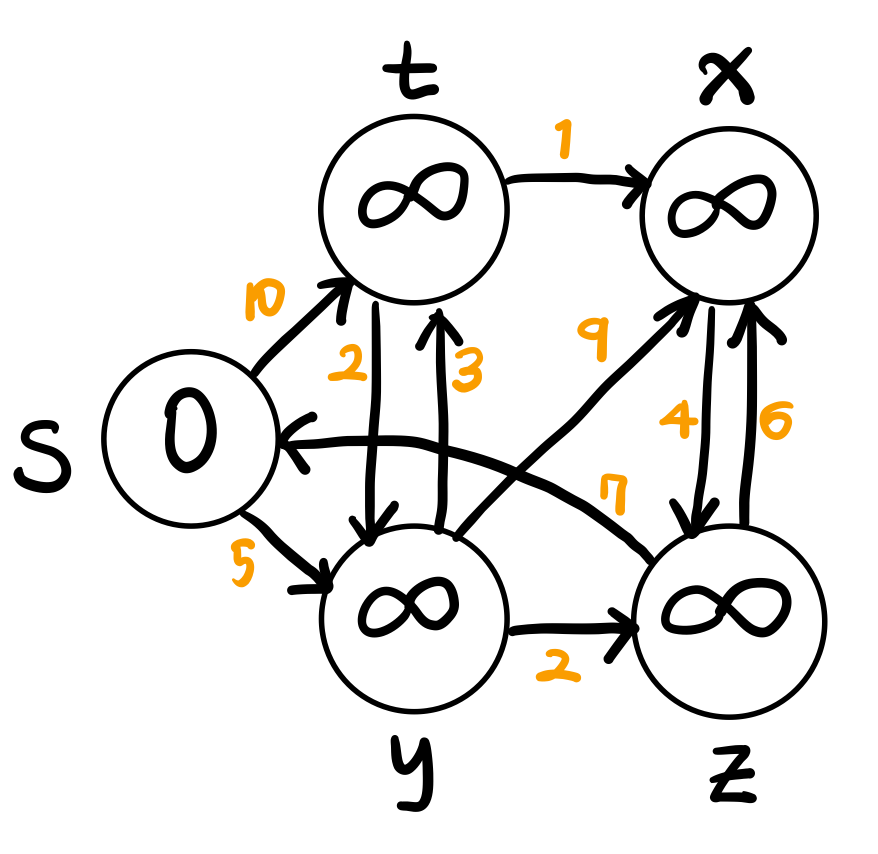
2.1. 예제


현재 Q에서 가장 작은 값을 찾는다 --> s


s의 인접 노드 중에서 더 작은 y 선택


y에서 relaxation 시행, 가장 작은 z 선택

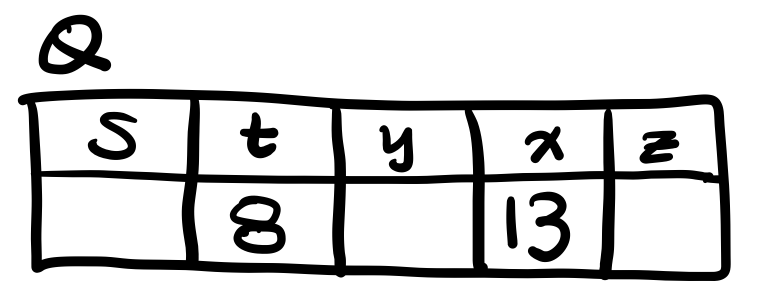
z에서 relaxation 시행, Q에서 가장 작은 t로 다시 돌아감
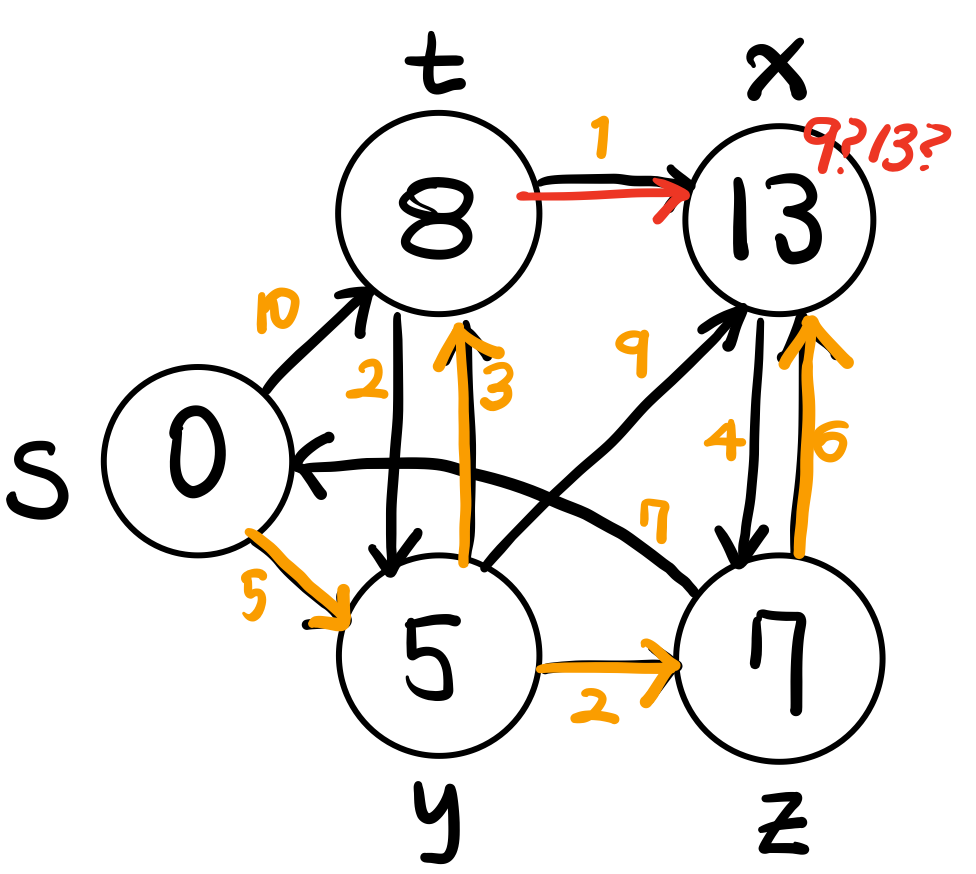
t에서 relax 시행했을 때 x로 가는 경로값이 업데이트 된다
2.2. 수행시간
배열로 구현한 경우 ---> O(V2)
힙으로 구현한 경우 ---> O(VlogV+ElogV)
피보나치 힙으로 구현한 경우 ---> O(VlogV+E)
'컴퓨터 > 알고리즘&자료구조' 카테고리의 다른 글
| 최소 신장 트리 구하기 : 크루스칼(Kruskal) 알고리즘 (0) | 2022.10.05 |
|---|---|
| 합집합 찾기(union-find) (0) | 2022.10.05 |
| 자료구조 : 힙(heap) (0) | 2022.09.27 |
| 최단 경로 문제: 벨만포드 알고리즘 (1) | 2022.09.26 |
| 빅오표기법(Big-O notation)과 시간복잡도 (0) | 2022.09.25 |