camera projection matrix : 3D space의 point --> 2D image plane 변환
모두 동차좌표계로 나타냄
변환의 두 factor : camera rotation & translation, pixel transformation/camera calibration matrix K
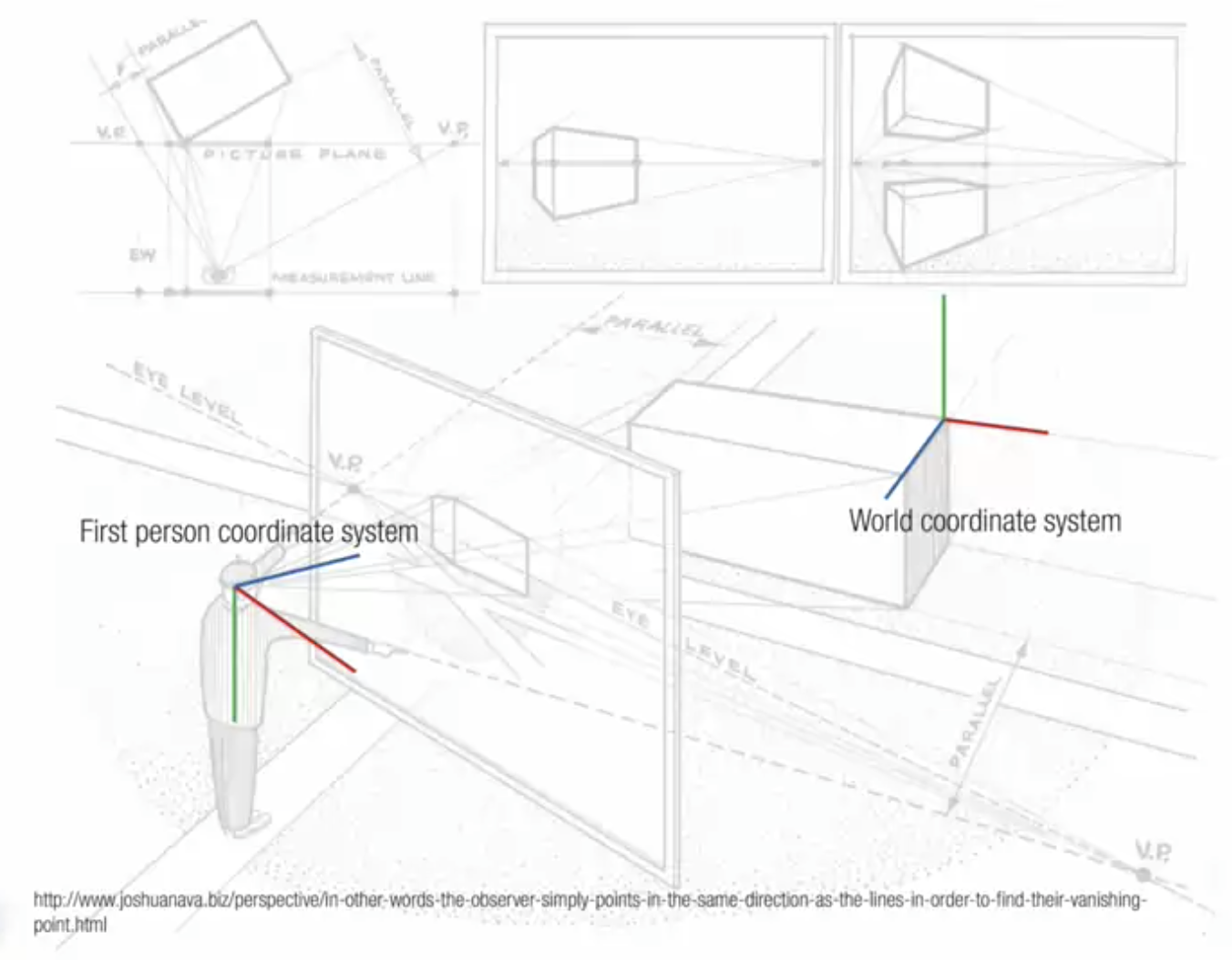
" 사진을 바라보되, 단순히 2D 이미지가 아니라 사람 앞에 카메라가 놓여 있다고 생각. 사람은 picture를 통해서 세상을 바라고 보고 있음. 2D plane의 점들에 있어서, 카메라맨과 그 점 사이에 선을 형성함. 그 ray는 3D space 에서 ray를 형성하고, 그 ray 의 집합은 physical space 의 평행선 집합에 해당하며, 무한대의 동일한 지점에 모두 수렴함. 그 무한대 점들이 2D plane으로 돌아와 project될 때, 동일한 점에 project 되는데, 그것이 소실점임."

두 개의 좌표계가 있음
1) 3rd person perspective, world cooridinate system
2) 1st person perspective, my coordinate system
- world에 대해서 fist person perspective 으로서 어디에 위치하는지
- space에서 어디를 향하고 있는지(oriented), world coordinate system에 상대적으로 XY포지션이 어떻게 되는지
- 즉, "where are we in the space?"
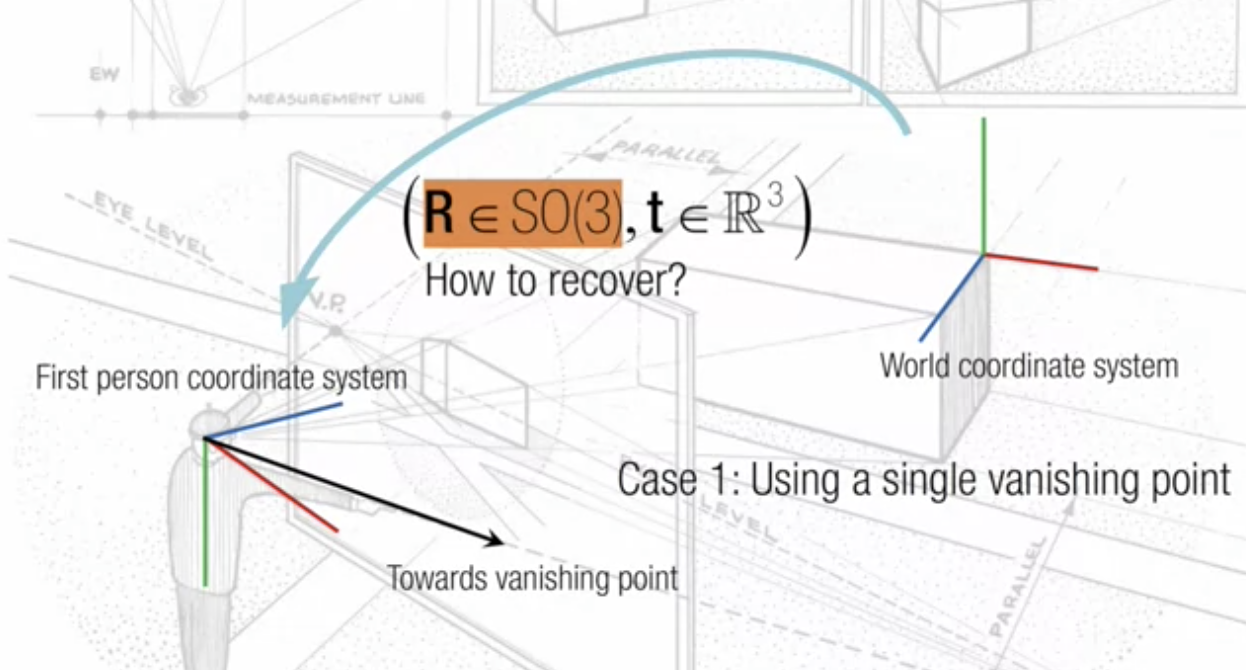
rotation matrix 를 어떻게 recover 할 수 있을까?
- translation 은 일단 무시하고, vanishing point를 활용한다
- rotation matrix에는 3차원의 방향이 있는데, 3D space에서 모든 축에 대한 상대적인 각도를 알아야 함
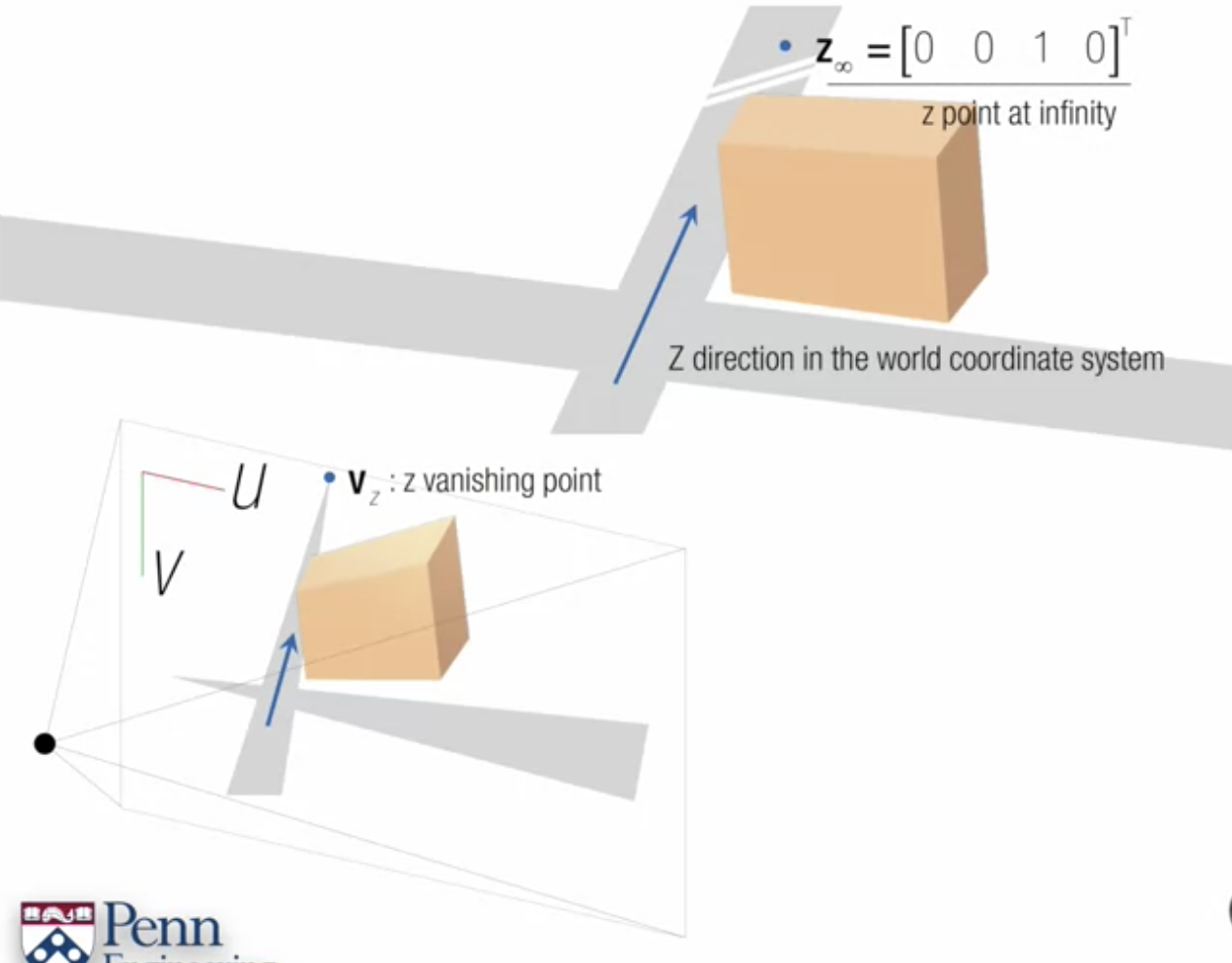
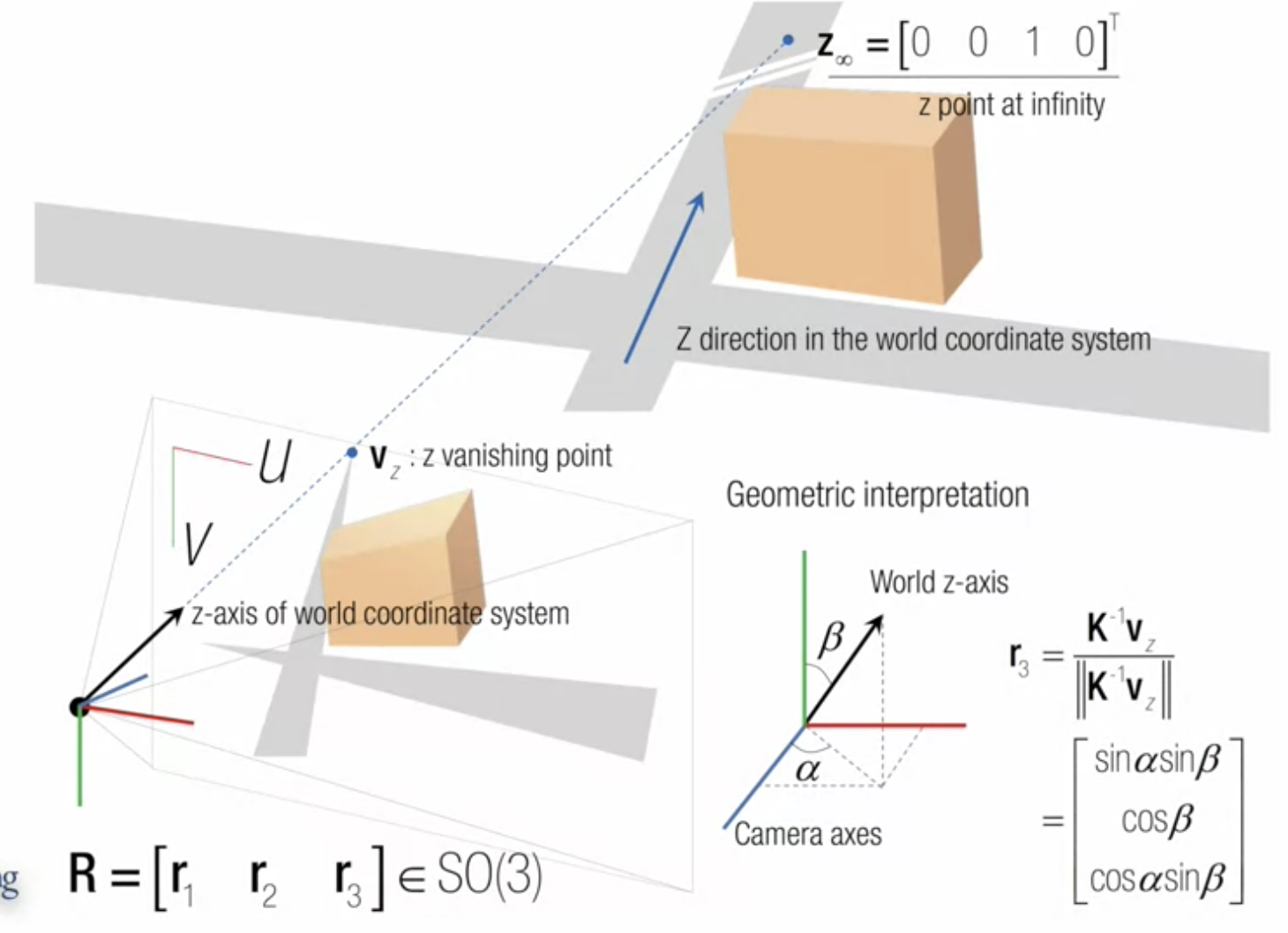
- vanishing point z in 3D world coordinate system
- X = 0, Y = 0, Z = 1
- point at infinity 임을 가리키기 위해 마지막 요소는 0
--> (0, 0, 1, 0)
- vanishing point z in 2D image
- z 방향이인 선들의 교차점에 의해 형성됨
- finite coordinate system 에서의 한 점 = vz
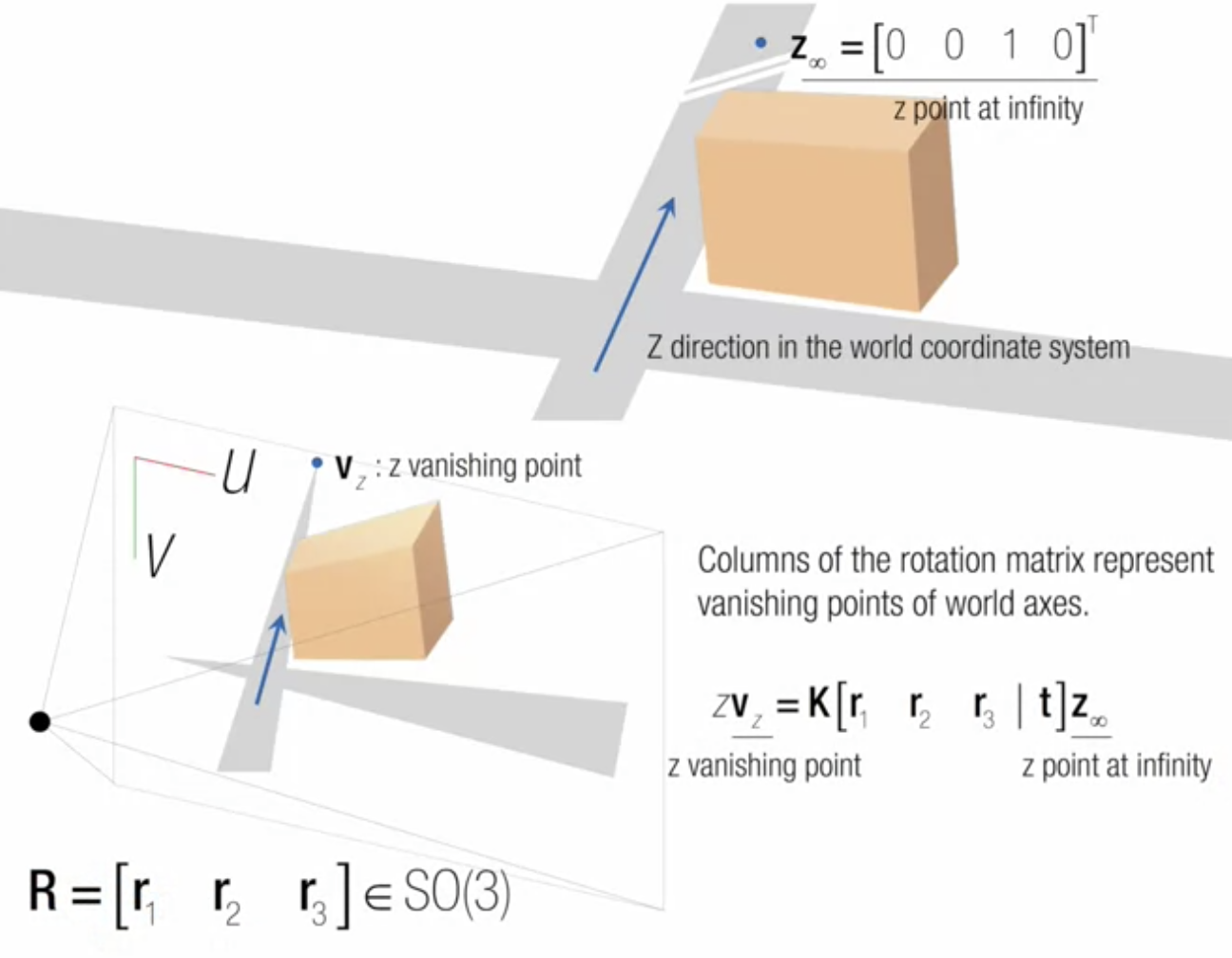
우측 하단 수식 확인
- z point at infinity 가 (0, 0, 1, 0) 이기 때문에 rotation matrix의 두 요소와 translation을 제거하게 됨: r3만 남음
- 즉, camera projection matrix의 네 열 중 세 열을 제거하게 됨
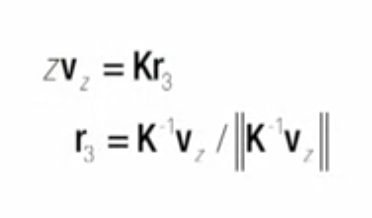
--> matrix K 가 r3(rotation의 세번째 열) 을 변형하는 것이 됨
--> 3D에서 Z 방향의 3차원 축이 있을 때, 이를 pixel space로 이미지화 하면 이 소실점을 xy 위치로 보게 됨; 다른 angle들, translation까지 사라짐
- 만약 카메라를 좌우상하로 움직여도 동일한 소실점은 그대로 유지
- r3를 구하기 위해서는 K 역행렬로 xy공간의 pixel 을 변환
- 이때 r3은 rotation matrix의 열이므로 "so it must have a normed one (?)"
- 이 벡터를 denormallize(비정규화) 하여 r3을 구할 수 있음
- 이 r3은 무슨 의미일까?
pan, tilt, yaw 용어 관련한 참고 자료!
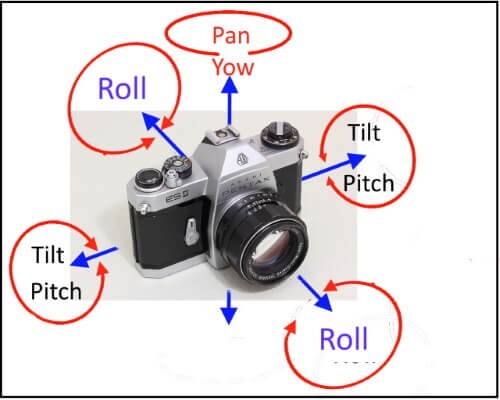
"Some of you might be familiar with the pan-tilt-yaw representation rotation. If I were flying a plane, I can see myself panning around, tilting up and down, and yawing in space."
world의 z축은 camera pan과 tilt 에 의해 transform 된다
α - pan
β - tilt
r3은 α, β 관점에서 아래 벡터와 같이 표현된다
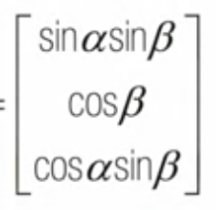
한편, yaw angle(rotation around z axis)도 평행선 집합으로 알아낼 수 있을까? no
- 왜냐하면 z 방향의 소실점이 주어졌을 때 소실점 z가 움직인다고 볼 수 없기 때문(?)
rotation의 모든 세 각도를 알아내기 위해서는 수직하는 두 소실점을 알아야 한다.
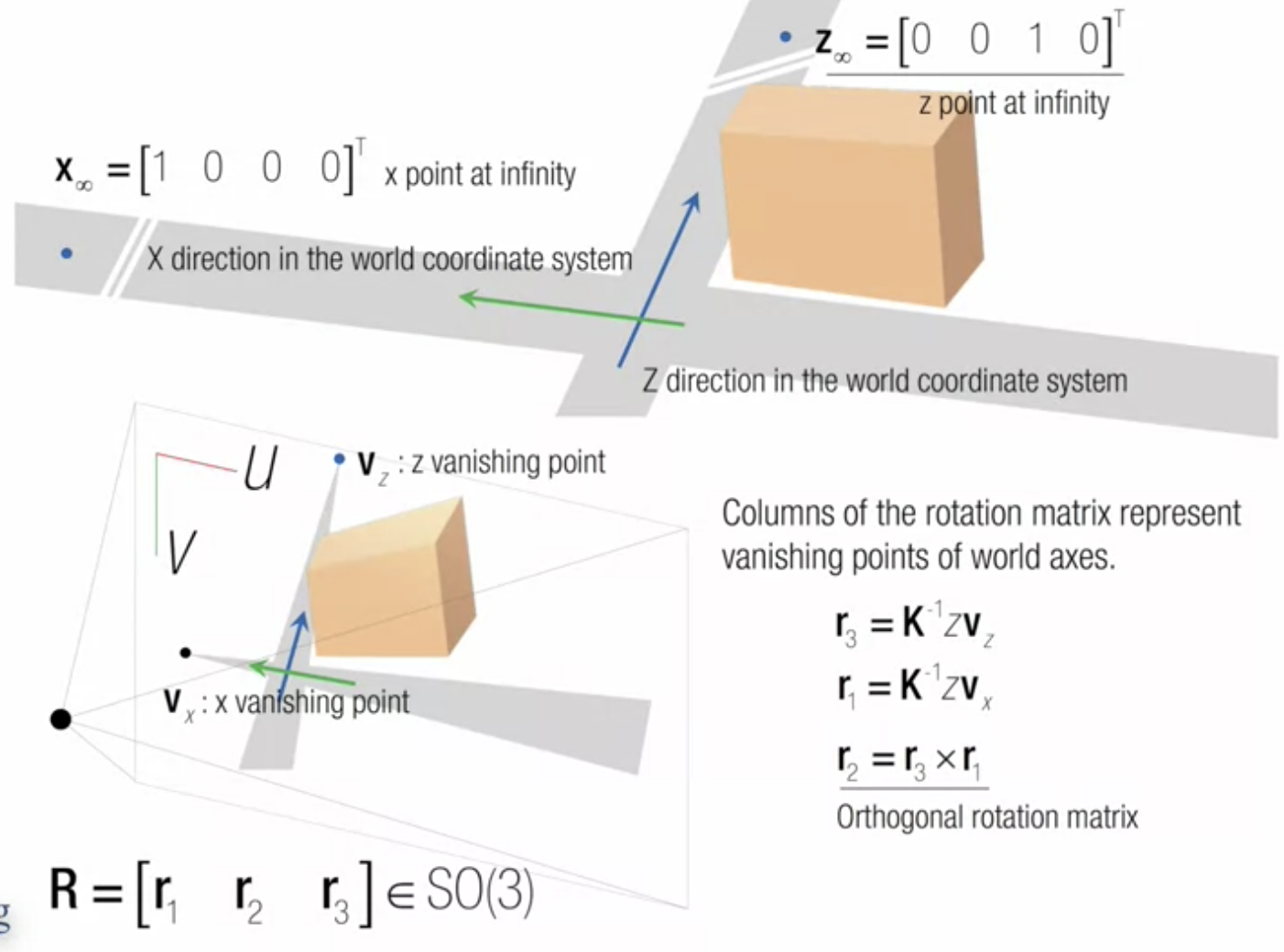
- 가로로 가로질러 가는 도로로 나타내지는 소실점이 하나 더 있음 -> x 방향으로 가는 소실점 형성
- r3 : vz 로 구할 수 있음 (z축 대응)
- r1 : K역행렬로 변환한 vx (x축 대응)
- x축과 z축이 수직 관계이므로
---> r2 = r1 * r3
-----> 두 개의 소실점을 통해 rotation matrix 를 완전히 복구함

- 역행렬 K 변환을 통해서 2D pixel coordinates를 optical world 에서 optical ray에 해당하는 ray 로 변환할 수 있음
- "Now we have a scale factor Z which needs to be taken out and this is easily done, because we know all the three columns r1, r2, r3 have normal one"
- normal one 갖도록 r1, r2, r3을 renormalize함
[Exercises]
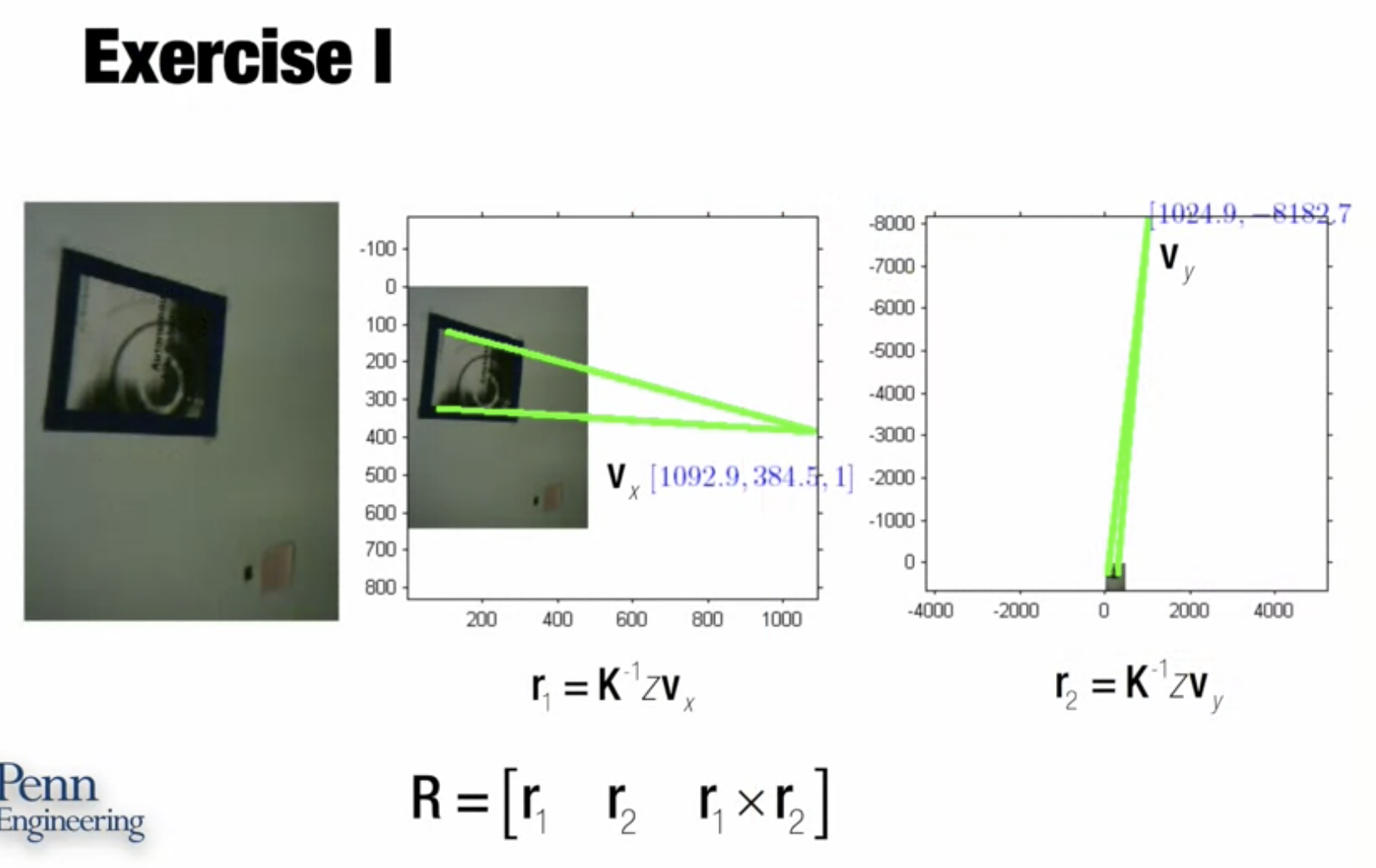
- 수평선 방향으로 소실점을 계산할 수 있으며, K 역행렬을 통해 소실점을 pixel coordinates에서 optical coordinates으로 변환할 수 있음
- y 방향으로도 소실점 계산
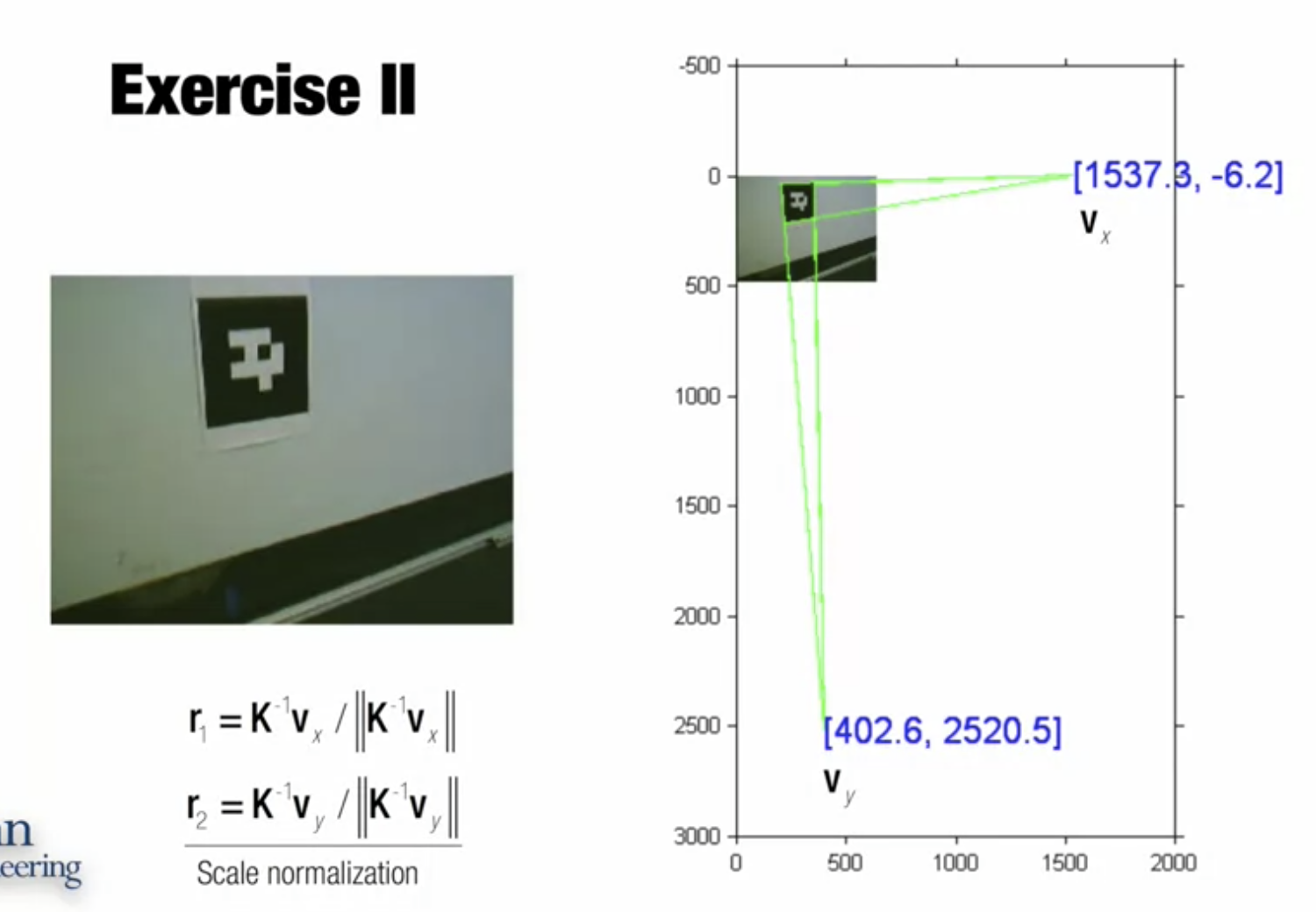
- norm one 갖도록 정규화 --> rotation matrix의 열들을 구했음
- 물리세계에서 서로 수직하는 선들이 필요함
--> rotation matrix의 모든 열값을 가지는 상태에서 camera pan-tilt 등 물리적 의미를 구할 수 있음
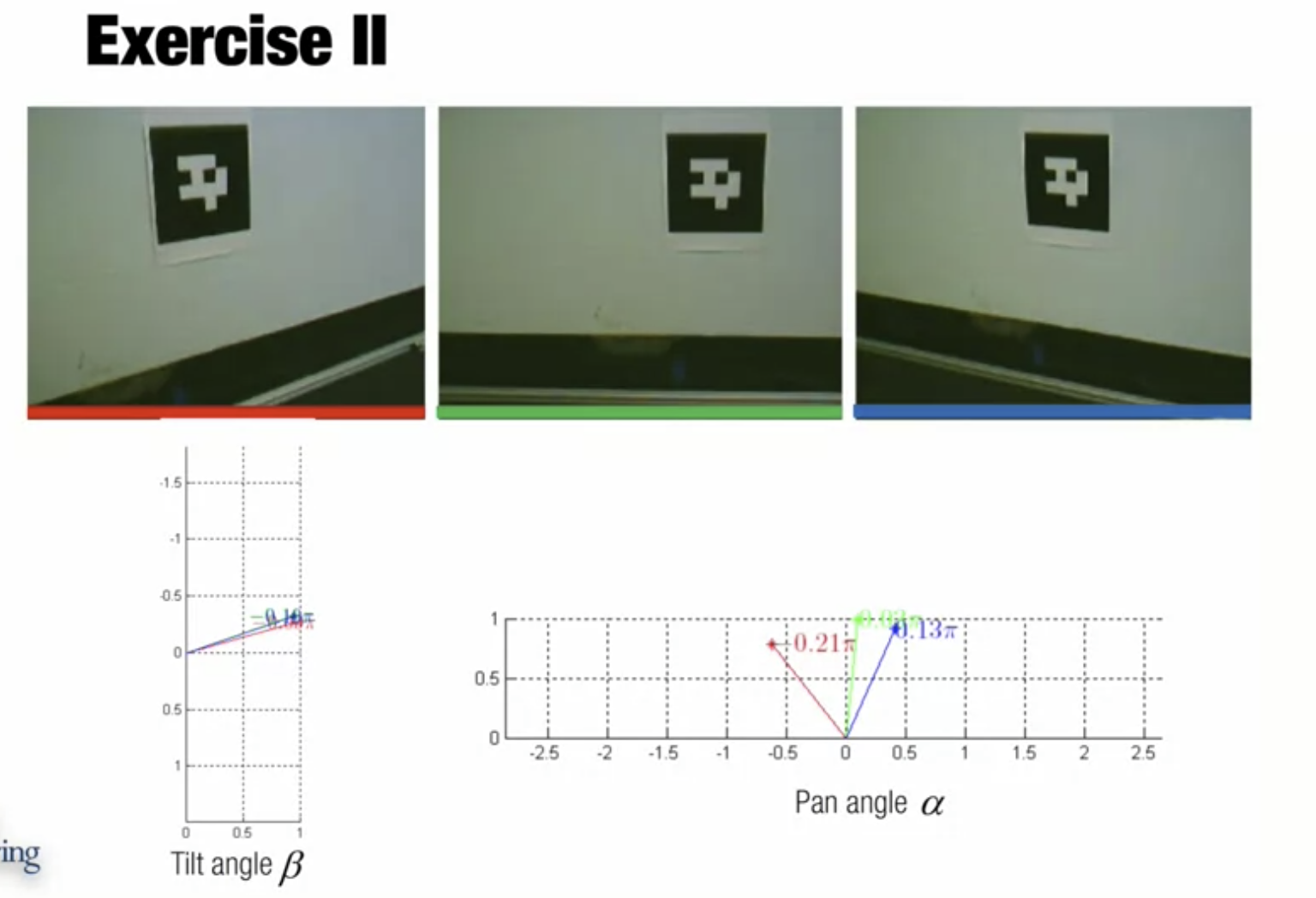
물리세계에서의 수직하는 두 선을 통해 world에 대한 camera의 상대적인 방향 구하기
여기에 더해 translation, 즉 카메라의 위치도 구할 수 있을까?
translation vector t도 구해보자
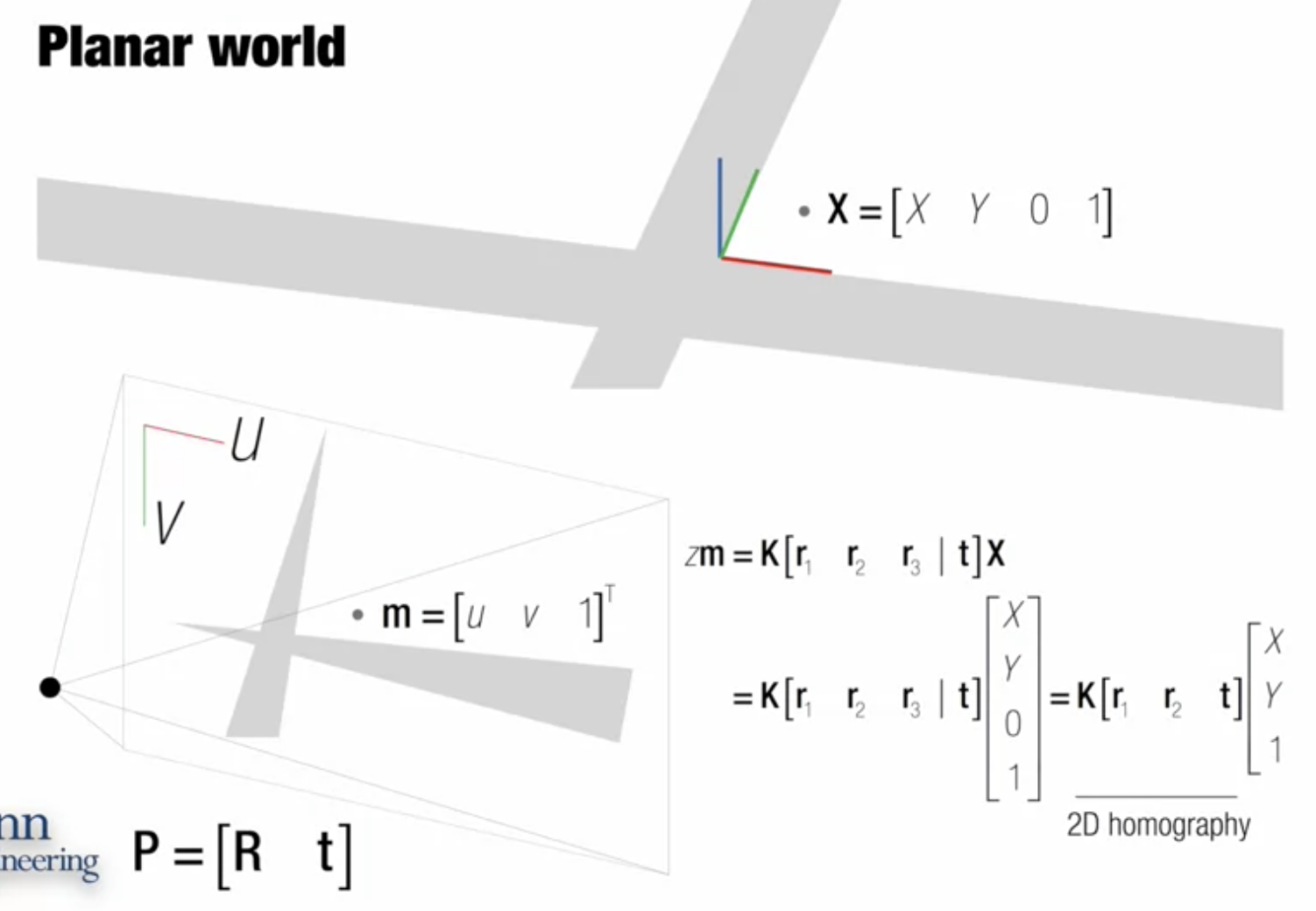
3D 세계를 보는 대신에 ground plane 을 바라보기로 함
이 경우 world coordinates는 (X, Y, 0, 1)이며 image로 project되었을 때는 동차좌표 (u, v, 1)
--> rotation 에서는 r3가 제거됨
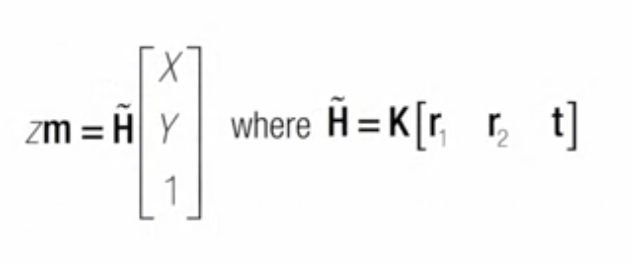
homography matrix H = K * r1, r2, t
H토타는 physical ground plane의 4 points 그리고 그에 상응하는 image plane 4 points로 근사할 수 있음
H토타를 구하면 rotation, translation을 추적, 구할 수 있음
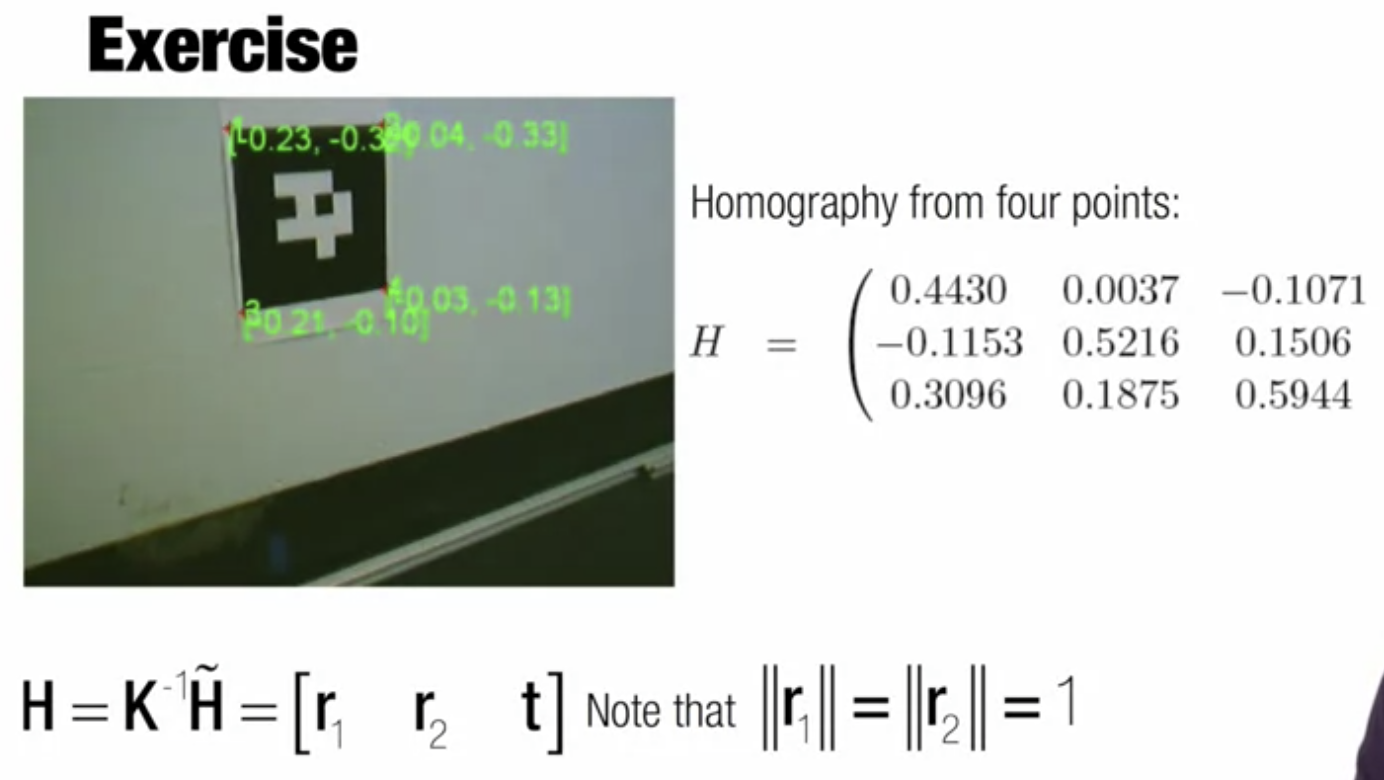
H토타에 K 역행렬 취하면 optical world 로 돌아가 H가 됨
- 즉, H = [r1, r2, t]
- 이때 r1, r2의 norm은 1
- r1, r2의 정규화를 통해 t 벡터를 찾을 수 있음
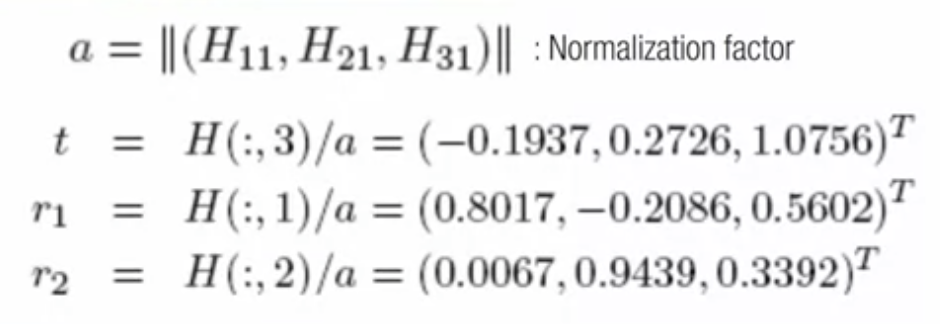
'인공지능 > pose estimation' 카테고리의 다른 글
| ROMP 이해하기 (0) | 2022.08.10 |
|---|---|
| Impersonator++ 이해하기 (0) | 2022.08.10 |
| Camera Calibration (0) | 2022.05.11 |
| How to Compute Intrinsics from Vanishing Points (0) | 2022.05.11 |
| 3D World to First Person Transformation (0) | 2022.05.10 |