Multiple View Geometry: 3rd person view measurement
- 동일한 오브젝트를 여러 다른 관점에서 보게 될 때
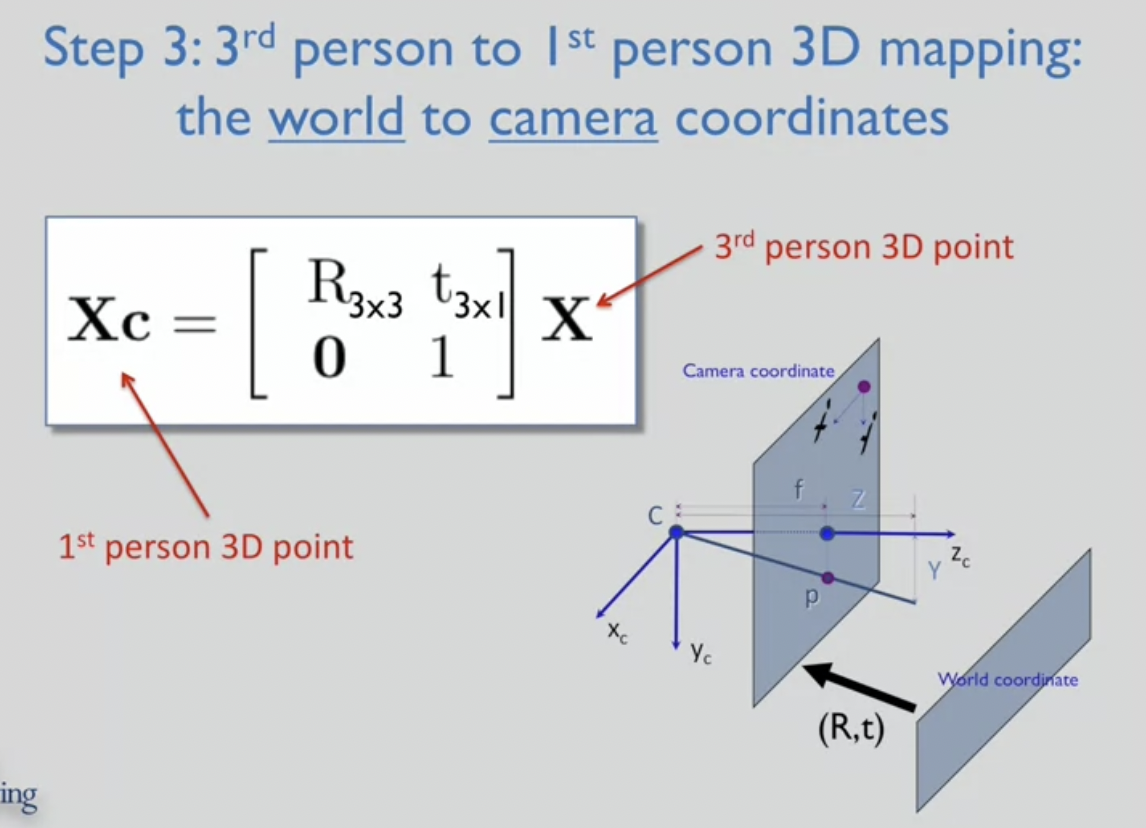
(step 3) : 3rd person to 1st person 3D mapping: the world to camera coordinates

- 3rd person 3D 좌표계에서 측정된 3D 공간의 point들
--> 불변함. 상수임.
- 바뀌는 것은? 1st person 관점에서 3D 벡터가 어떻게 보이는지
--> 3rd person 3D point 들을 1st person 으로 변환해야 함
- Rotation: 좌표계의 변화
- Translation : world center를 camera center로 변환
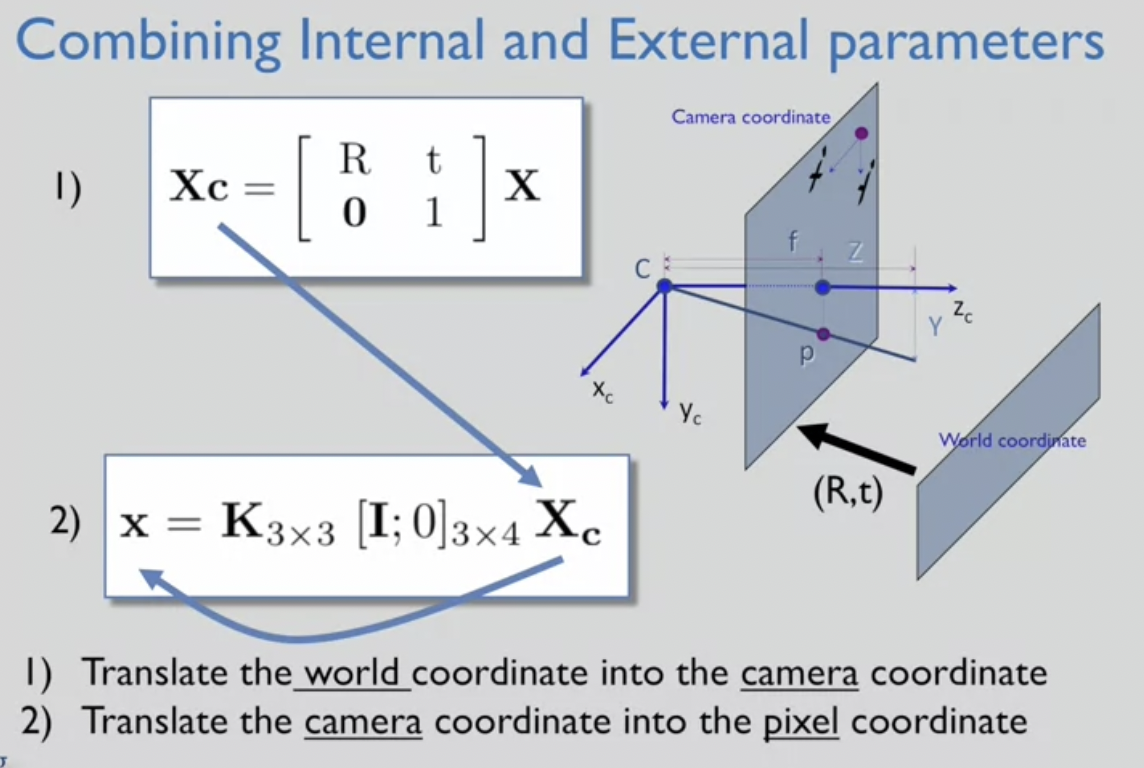
이러한 방식으로 최최종..
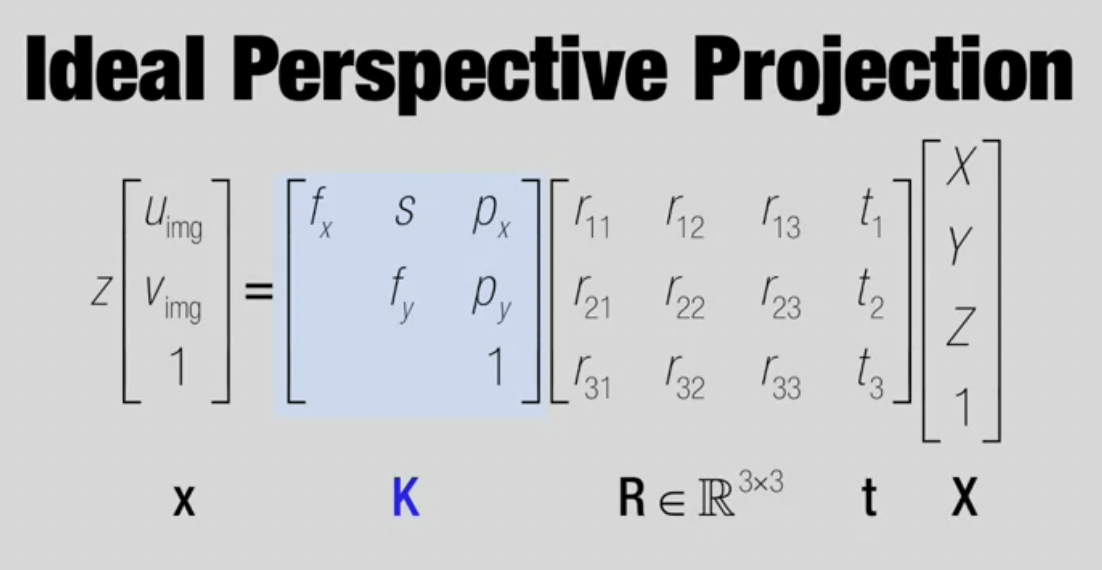
- X, Y, Z : world coordinate system, 3rd person perspective, 상수
- rotation matrix + translation vector : 3rd person perspective의 point measure를 '나'를 중심으로 한 1st person coordinate system으로 변환
- calibration matrix K : 픽셀 공간 상 2D image 형성
각자가 다른 관점에서 세상을 바라보고 있는데, 최종 x는 '내 관점에서 보는 세상'이며, 내가 이 공간에서 어디를 향하고 위치하는지에 따라 X, Y 위치가 달라질 수 있음
[speical cases]
1) 3D 오브젝트가 평면 오브젝트일 때

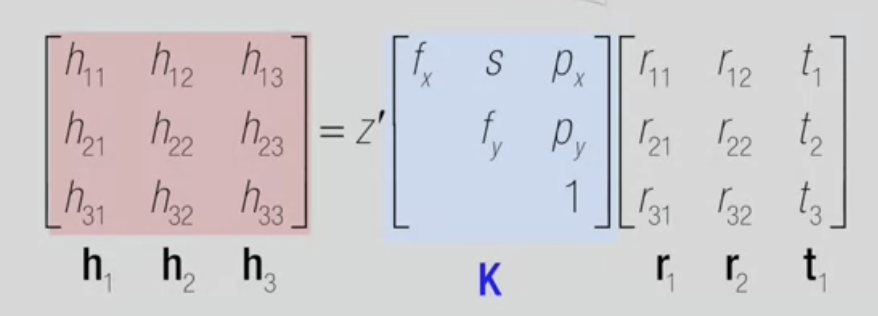
- 3D 좌표 X, Y, Z가 모두 plane 위에 있음
- X, Y가 오브젝트의 plane 그리고 Z를 그 plane에 수직하는 것으로 볼 수 있음
--> plane 위 어떤 point든 Z가 0인 특성을 가지게 됨
- rotation matrix의 첫 두 열 + translation vector로 된 행렬에 K행렬을 활용해 3x3 행렬로 인코딩
--> 3D의 평면 오브젝트를 image plane으로 변환
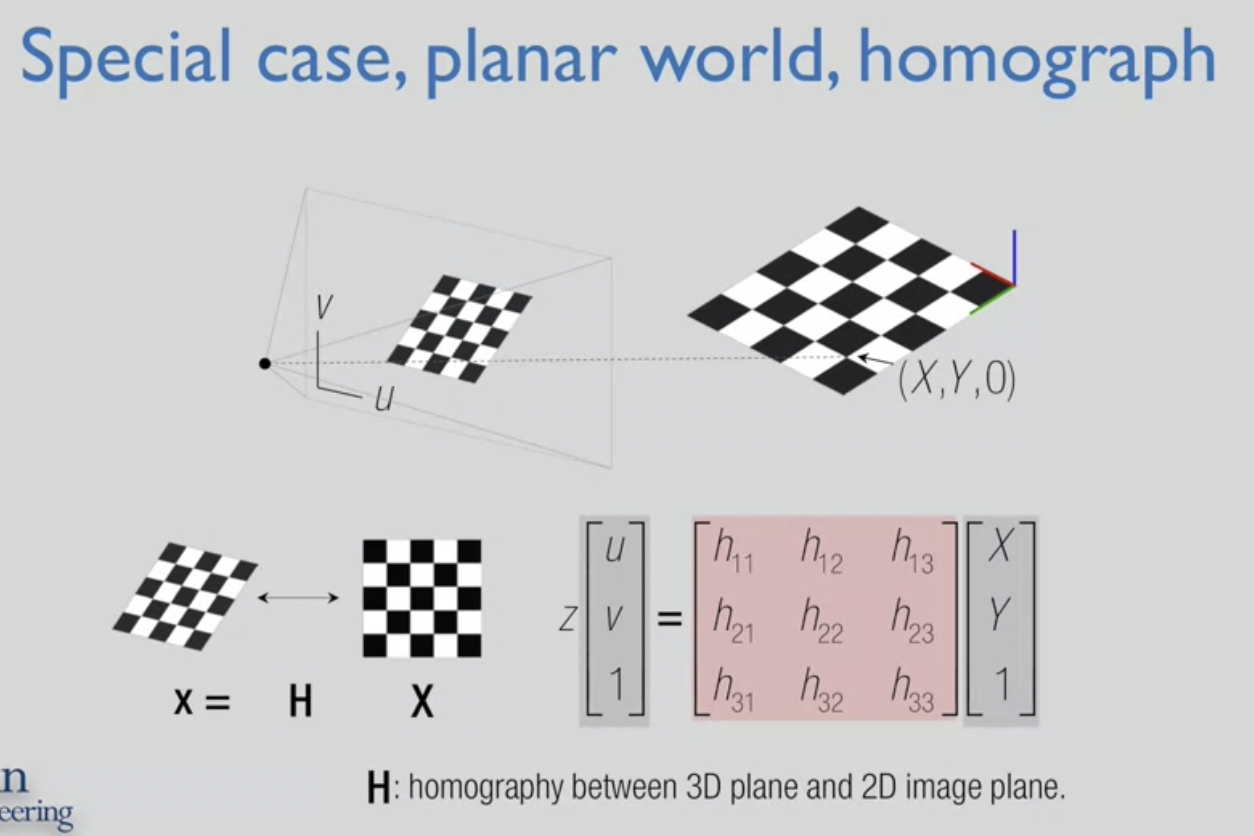
- 물리적인 3D plane에 있는 (X, Y) 좌표
- 3x3으로 된 행렬로써 변환됨
--> plane에서 추출한 이미지는 카메라 방향에 따라 왜곡되어 있을 수 있음
- Z: 위 식에서 Z는 모든 픽셀에 대해 의존적
--> homography transformation
2) 카메라가 회전함
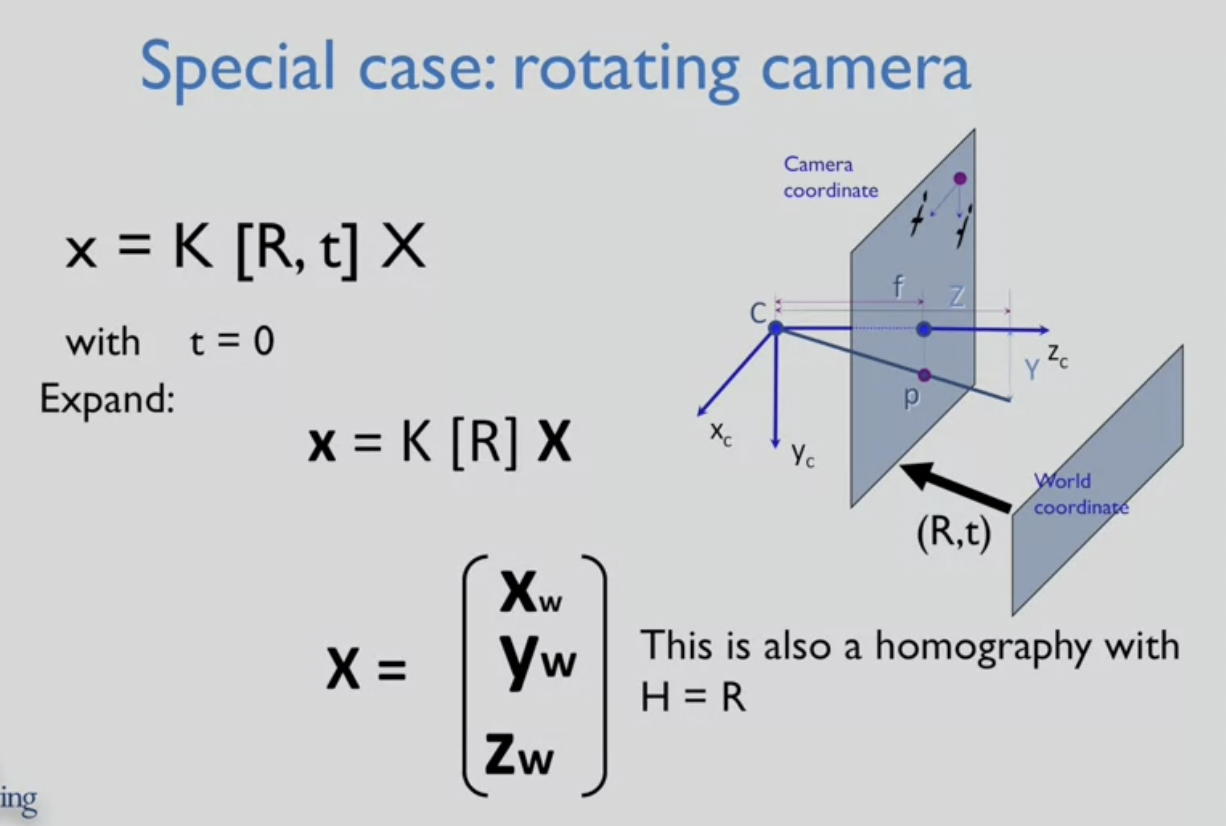
- 이 경우 T 벡터는 0 : optical center를 이동하는 것이 아니기 때문
--> (X, Y, Z, 1) 에서 마지막 요소를 제거하게 됨
--> K(3x3) * R(3x3) * (X, Y, Z)
'인공지능 > pose estimation' 카테고리의 다른 글
| Camera Calibration (0) | 2022.05.11 |
|---|---|
| How to Compute Intrinsics from Vanishing Points (0) | 2022.05.11 |
| Pinhole Camera Model/Focal Length and Dolly Zoom Effect/Intrinsic Camera Parameter (0) | 2022.05.10 |
| Rotations and Translations (0) | 2022.05.09 |
| Point-line Duality (0) | 2022.05.09 |