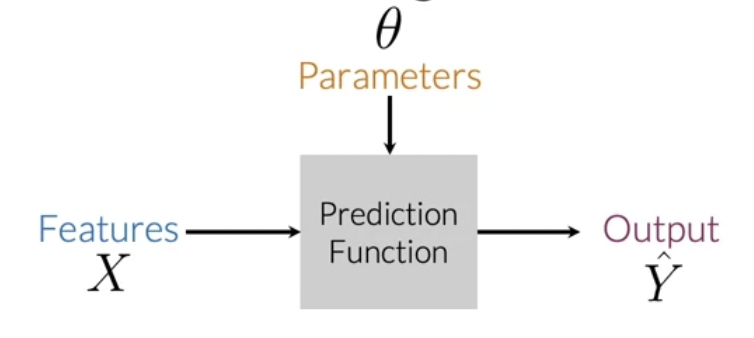
Supervised ML & Sentiment Analysis
logistic regression(로지스틱 회귀) 을 적용하기
[Supervised ML(training)]

Labels Y (expected value)와 predicted output Y햇이 얼마나 비슷한지 비교하는 cost funtion
cost가 최소화될 때까지 파라미터를 수정하며 업데이트
[Sentiment analysis]
- negative : 0
- positive : 1
--> Logistic Regression : 두 개의 클라스 중 하나로 분류
Logistic Regression Classifier
1) raw 학습셋에서 useful feature 로 추출
2) classifier 학습
3) 예측
Vocabulary & Feature Extraction
텍스트를 vector로 표현하기
사전을 구축, array of number로 인코딩
1) 트윗의 리스트
[twt_1, twt_2, ..., twt_n]
(ex. I am happy because I am learning NLP)
2) 사전 V
list of unqiue words
3) Feature Extraction
트윗에 나타난 어휘를 1로 표시, 그 외는 0
--> sparse representation
- 사전의 크기만큼 큰 개수의 feature를 가짐. 너무 큼.
Negative and Positive Frequencies
positive 클래스에 특정 단어가 등장한 횟수가 궁금할 수 있음
--> 이러한 횟수를 통해 feature extraction 할 수 있음

이러한 말뭉치 데이터가 있다고 해보자
클래스별로 어휘의 빈도수를 카운트할 수 있음 = frequency dictionary

Feature Extraction with Frequencies
전체 말뭉치 사전 대신에 3차원(3개 feature)으로 feature extraction 하는 방법
[Feature Extraction]

- bias unit
- the sum of pos/neg frequencies for every unique word on the tweet


따라서 벡터 Xm = [1, 8, 11]
Preprocessing
- stemming
- stop words
[stop words & punctuation]

- punctuation 이 중요한 정보를 전달하기도 함
[stemming and lowercasing]
- 어간 분리, 소문자화
Putting it All Together
x matrix 생성하기

m개의 트윗 집합을 전처리 하여, 트윗 하나당 하나의 리스트를 이루는 집합을 구성해야 함
그 다음 frequencies dictionary mapping 을 활용해 feature extraction 함


matrix X (m개 행, 3개 열)
[implementation]
freqs = build_freqs(tweets, labels)
X = np.zeros((m, 3))
for i in range(m):
p_tweet = process_tweet(tweets[i])
X[i, :] = extract_features(p_tweet, freqs)X matrix를 logistic regression classifier에 입력시키기
Logistic Regression Overview
logistic regression

F = sigmoid function
logistic regression에서 분류하는 데 사용되는 함수 h <-- 시그모이드 함수


- x(i) : features vecter X
- i : i번째 observation / data points (i번째 트윗)
- 오른쪽 시그모이드 함수 그래프
- θT * x(i) 가 마이너스 무한대로 갈수록 0이 되고
- 플러스 무한대로 갈수록 1이 됨
- 분류 문제에 있어서 threshold가 필요함
- 보통은 0.5로 세팅됨
- θT * x(i) = 0 일 때 ㅇㅇ

- 내적의 결과가 0보다 크거나 같으면 예측 결과는 positive가 됨 - 내적의 결과가 0보다 작으면 negative가 됨

- logistic regression의 notation을 이용해서 가중치 θ를 학습하는 데 사용할 수 있음!
Logistic Regression: Training
- θ 변수를 찾아보자
- cost funtion을 최소화하는 θ를 찾을 때까지 학습 iteration을 돌린다
- 파라미터 θ1, θ2에 따라 cost function이 달라진다고 가정해보자

1) initialize 파라미터 벡터 θ

2) cost function의 그라디언트 방향에 따라 θ를 업데이트 한다
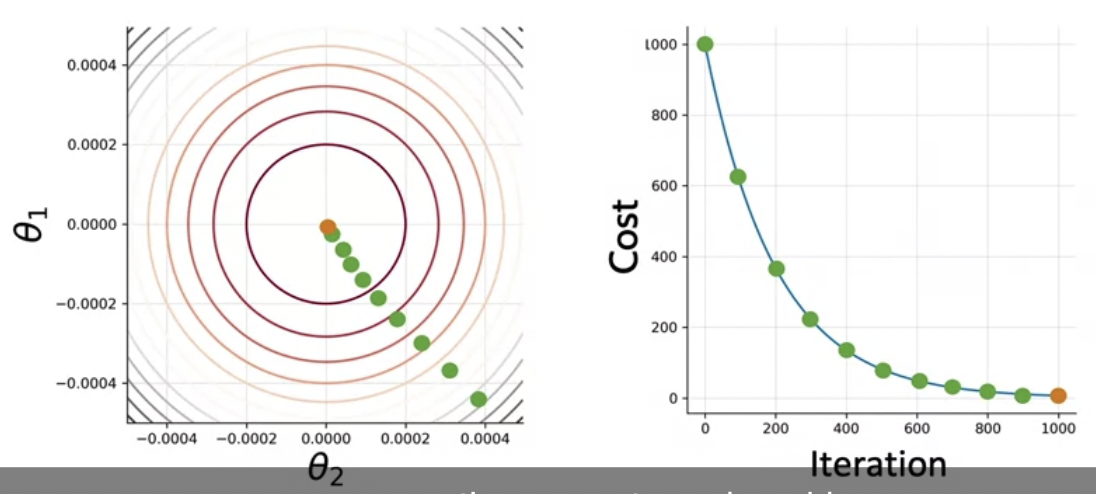
[상세 과정]

- 각 observation에 대한 값을 logistic function으로 구한다
- 그로써 cost function의 그라디언트를 구할 수 있게 된다
- 파라미터를 업데이트 한다
- cost J 를 구하고 나면 훈련이 더 필요할지 stop-parameter나 최대 훈련횟수에 따라 결정한다
---> gradient descent(경사하강법)
Logistic Regression: Testing
새로운 데이터로 모델을 테스트하기 (정확도 계산)
- X_val, Y_val, 학습된 θ 준비
- X_val, θ 에 대해 시그모이드 함수값을 구함
- 이 값이 threshold값보다 크거나 같은지 확인
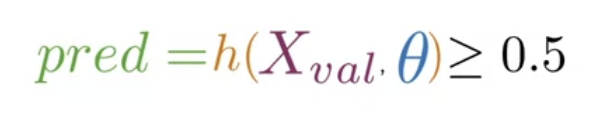

- 예측 벡터를 생성
- 검증셋의 라벨과 비교 (정답이면 1, 틀리면 0), 검증셋 개수로 나누기

Logistic Regression: Cost Function
- 로지스틱 회귀의 손실함수

- m개 값을 더한 다음 m으로 나눈다? --> some kind of average
- 두 개 항을 더한다
1) y(i) * log h(x(i), θ) : 예측결과h(x(i), θ)의 로그값에 라벨값을 곱함
- y(i) 즉 라벨값이 0 이면 로그값이 어떤 것이든 0임
- y(i) 라벨값이 1이고, 예측값이 0.99이면(1에 가까우면), 로그값은 0에 가까워지므로 결과는 0에 가까움
- y(i) 라벨값이 1이고, 예측값이 0에 가까우면, 결과는 마이너스 무한대
- 즉 이것은 y(i)가 1일 때 유의미하며, 예측값이 라벨값(1)에 가까워질 때 손실이 작아짐
- y(i)가 1인데 예측값이 0에 가까우면 손실이 무한대가 됨
2) (1 - y(i)) * log (1 - h(x(i), θ))
- y(i) 즉 라벨값이 1일 때 로그값이 어떤 것이든 0임
- y(i) 라벨값이 0이고, 예측값이 0에 가까우면 결과는 0에 가까움
- y(i) 라벨값이 0이고, 예측값이 1에 가까우면 결과는 마이너스 무한대
--> y(i) 라벨값이 1일 때 유의미해지는 항과 라벨값이 0일 때 유의미해지는 항의 합
--> 음수의 log 값이므로 (진수가 예측값이므로 1이하) (-1)를 곱해 늘 양수값을 가지게 한다


Optional Logistic Regression: Gradient
경사하강법의 정의
(파라미터 θ에서 손실함수의 편미분값을 뺀다)

이를 미분하여 (밑에 자세한 설명 있음)

이를 벡터로 나타내면

[cost function J(θ)에 대한 편미분]
1) 먼저 시그모이드 함수 h(x) 에 대한 편미분 식을 세운다

이때 θj에 대하여 h(x(i),θ)를 미분한다고 한다면

2) J(θ)을 편미분 해본다


'인공지능 > Natural Language Process' 카테고리의 다른 글
| Natural Language Processing with Classification and Vector Spaces: sentiment analysis with Naive Bayes(1) (0) | 2022.05.24 |
|---|---|
| Logistic Regression 퀴즈 풀이 (0) | 2022.05.22 |
| Natural Language Processing 특화 과정 (0) | 2022.05.19 |
| [번역] cyBERT (0) | 2021.04.22 |
| [미니 실습] 뉴스 기사에서 주요 키워드 추출하기 (0) | 2021.03.11 |