보충 지식
Shannon-Nyquist 정리, Aliasing …
https://blog.naver.com/sdj9604/222192630938
https://m.blog.naver.com/wyepark/221013968332
- 디렉 델타 함수(Dirac Delta Function) - “신호 처리 분야에서는 임펄스 함수라고 부르기도 한다”
- Shannon-Nyquist 정리
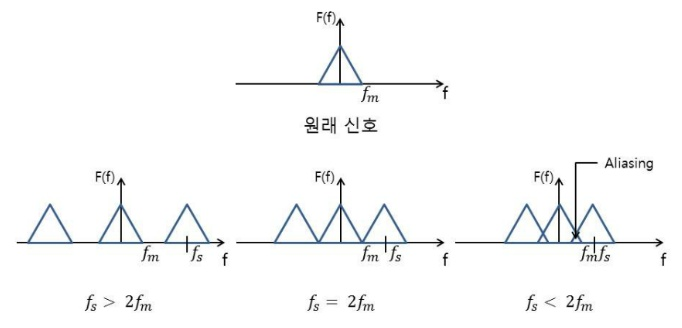
- 모든 신호는 그 신호에 포함된 가장 높은 진동수의 2배에 해당하는 빈도로 일정한 간격으로 샘플링하면 원래 신호를 완벽하게 기록할 수 있다. (ex. 1초에 10번 진동하는 신호는 0~1초 가로축을 20조각으로) (출처 https://blog.naver.com/pertisia/222109181860 )

- convolution 연산의 equivariance
- Convolution 연산은 translation equivariance 특성을 갖고 있다. Equivariance란, 함수의 입력이 바뀌면 출력 또한 바뀐다는 뜻이고, translation equivariance는 입력의 위치가 변하면 출력도 동일하게 위치가 변한채로 나온다는 뜻이다. (출처 https://seongkyun.github.io/study/2019/10/27/cnn_stationarity/ )
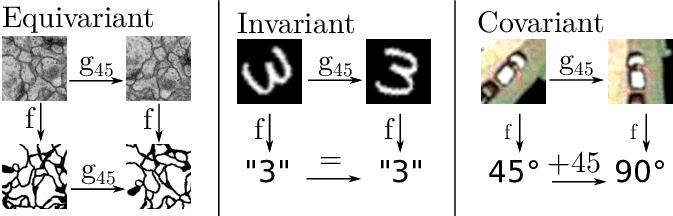
- sinc function (싱크함수)
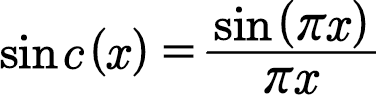
- Dirac comb(디락 빗) Ш

- 이산화(discretization) = 샘플링
- 항등 작용(Identity operation) = 어떤 수에 연산을 시행한 결과가 처음의 수와 동일하도록 만들어 주는 연산
- interleaving 에 대한 컨셉적(?) 이해
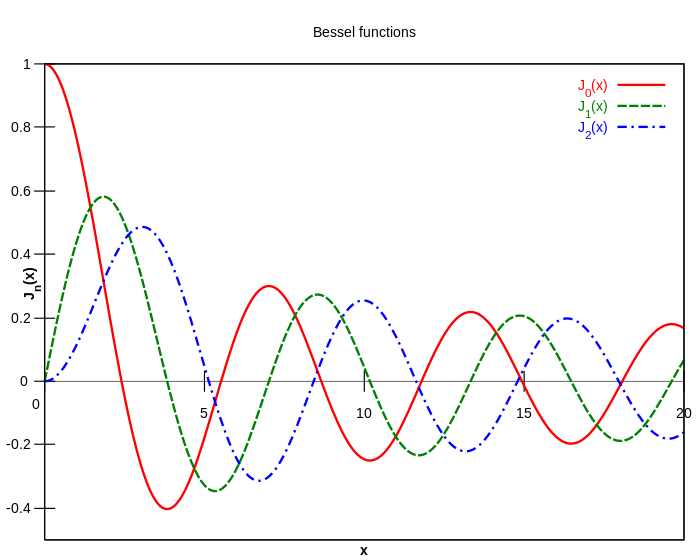
- Bessel function(베셀 함수)
-
α가 임의의 복소수일 때, 베셀 방정식의 가장 기본적인 해를 제1종 베셀 함수 Jα(x)라고 함
-
- commute
- ideal low-pass filter 와 관련하여 : https://kylog.tistory.com/36
- Fourier Features
- Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains (NeurIPS 2020 spotlight)
- https://youtu.be/iKyIJ_EtSkw
초록
GAN의 hierarchical convolutional 한 특성에도 불구하고, 합성 과정이 절대적인 픽셀 좌표계(absolute pixel coordinates)에 의존하고 있음을 확인함. detail이 객체의 표면이 아니라 이미지 좌표계에 고정된 듯한 모습으로 나타남. 근본적인 원인을 추적해보니 careless한 신호 처리가 생성기 네트워크에서 aliasing을 발생시킴. 네트워크의 모든 신호들을 연속적으로 해석함으로써 불필요한(unwanted) 정보가 계층적 합성 과정에서 유출되지 않도록 하는 아키텍처의 변화를 유도함. 수정된 네트워크의 FID 지수는 기존 StyleGAN2와 일치하나, internal representation에 있어서 매우 차별화됨. subpixel 스케일에서도 변환과 회전이 완전하게 동등하게 이루어짐. 비디오 및 애니메이션에 적합한 생성 모델로의 길을 개척함.
Introduction
- GAN의 합성 과정에 있어서 기반적 이해가 부족
- 실세계에서 여러 스케일에 걸친 디테일들은 hierarchically(계층적으로) 변화함
- (예) 머리가 움직이면 코도 움직이고, 코가 움직이면 모공이 움직임
- GAN 생성기의 구조가 이와 유사함
- coarse, low-resolution feature는 upsampling 레이어에 의해 계층적으로 정제되고(refined), convolutions에 의해 지역적으로 섞이게 되며(locally mixed), 비선형성nonlinearities을 통해 새로운 디테일이 도입됨(introduced)
- 이러한 표면적 유사성에도 불구하고, 현재 GAN 아키텍처는 이미지들을 자연스러운 계층적 방식(natural hierarchical manner)으로 합성하지 못함:
- coarse feature는 세부적인 feature의 정확한 위치가 아니라 그것의 존재 유무를 주로 통제함
- 대부분의 세부 디테일들이 픽셀 좌표계에 고정된 모습으로 나타남
- 이러한 “texture sticking” 현상은 latent interpolation에서 명확하게 보임; 객체가 공간에서 완전하고 일관성 있게 움직이는 느낌을 깨트림
- 본 논문은 오롯이 기저에 있는 coarse feature에 의해 각 feature의 정확한 sub-pixel 위치가 통제되어(inherited) transformation 계층이 더욱 자연스럽게 나타나는 아키텍처를 목표함
- 현재 네트워크가 이상적인 hierarchical construction을 부분적으로 건너뛸 수 있음을 확인
- by drawing on unintentional positional references available to the intermediate layers through image borders, per-pixel noise inputs and positional encodings, and aliasing
- 미묘하고 치명적인 이슈였던 aliasing은 GAN 연구에서 거의 주목받지 못했음
- Aliasing의 두 가지 출처를 밝혀냄
- 1) nearest, bilinear, strided convolutions 과 같은 비전형적인 upsampling 필터가 만들어낸 pixel grid의 희미한 잔상
- 2) ReLU, swish와 같은 nonlinearities의 pointwise 적용
- 네트워크는 아주 작은 양의 aliasing도 극대화하게 되고, 여러 스케일에 걸쳐 이를 결합한 결과 화면 좌표계에 고정된 텍스쳐 무늬(texture motif)를 기본적으로 깔게 됨
- 딥러닝에 일반적으로 쓰이는 모든 필터뿐만 아니라 이미지 처리에 쓰이는 high-quality 필터들에도 해당
- 어떻게 불필요한(unwanted) 부가정보를 제거하여 네트워크가 이를 사용하지 않게 할 수 있을까?
- border의 경우 사이즈가 살짝 큰 이미지를 사용함으로써 해결할 수 있지만, aliasing은 더 어려운 문제
- aliasing은 대부분 고전 Shannon-Nyquist 신호 처리 프레임워크에서 다뤄지는 문제임을 강조
- 별개의 샘플 그리드(discrete sample grids)로만 표현되는 연속적인 도메인에 적용되는 대역폭이 제한된 함수(bandlimited function)에 집중
- positional references의 모든 출처를 성공적으로 제거한다는 것은 detail들이 픽셀 좌표계와 상관없이 동등하게 잘 생성된다는 의미이며, 이는 곧 모든 레이어에서 연속적인 equivariance를 sub-pixel 변환(또는 회전)에 강제한다는 의미
- 이를 위해
- 1) StyleGAN2 생성기의 모든 신호 처리 요소를 포괄적으로 점검
- 2) 현재의 upsampling 필터가 aliasing을 억제하기에 충분히 aggressive하지 않으며 100 데시벨 이상 감쇠(attenuation)된 extremely high-quality 필터가 필요함을 발견함
- 3) 나아가 pointwise nonlinearities 으로 인해 발생하는 aliasing에 대해 원칙적인 해결책 제시, 연속적인 도메인에서 일으키는 효과를 고려하여 그 결과를 적절한 저주파(low-pass)로 필터링
- 4) 1x1 convolutions를 기반으로 하는 모델로 강력한 rotation equivariant 생성기를 구축할 수 있음
- aliasing이 적절하게 억제되어 모델로 하여금 더 자연스러운 계층적인 refinement를 강제하게 된다면, 모델의 운용 방식이 급격하게 변화함
- 새로운 internal representations - 디테일들이 underlying surface에 올바르게 붙어있도록 하는 좌표 시스템을 포함
- FID 지수 측면에서는 StyleGAN2와 일치하며 컴퓨팅 연산량은 살짝 무거움
- 최근 연구에서 CNN의 translation equivariance 부족이 다뤄져 옴
- 이러한 연구에서 다뤄진 antialiasing measure를 보다 자세하게 다루고, 이미지 생성 방식에서 근본적인 변화를 이끌어냄을 보여줌
- Group-equivariant CNN : generalize the efficiency benefits of translational weight sharing to, e.g., rotation and scale
- 1x1 convolution : 연속적으로 E(2)-equivariant한 모델의 객체, channel-wise ReLU nonlinearities와 modulation 과 호환될 수 있음
- Dey et al. 은 90° rotation-and-flip equivariant한 CNN을 GAN에 적용함으로써 데이터 효율성을 보여줌 → 본 연구는 효율성보다 보완(complementary) 측면에 집중
- 최근 implicit network는 1x1 convolutions 통해서 각 픽셀을 독립적으로 생성함
- 이러한 모델들은 equivariant 하지만 texture sticking 을 해결하지 못함; upsampling hierarchy 를 사용하지 않거나, 얕고 antialiasing 되지 않은 것을 사용하기 때문
Equivariance via continuous signal interpretation
- 네트워크를 따라 흐르는 신호가 무엇인지 다시 생각하기
- 데이터는 픽셀 그리드의 값으로 저장되어 있을지 몰라도, 이러한 값들을 신호로 그대로 표현할 수는 없음
- Doing so would prevent us from considering operations as trivial as translating the contents of a feature map by half a pixel (pixel의 절반만 이해하게 된다)
- Nyquist-Shannon 표본화 정리(sampling theorem)에 따르면, 규칙적으로 샘플링된 시그널은 어떠한 연속적인 신호도 표현할 수 있음; 0 ~ sampling rate*1/2 사이의 주파수들을 포함함
- two-dimensional discretely sampled feature map Z[x] that consists of a regular grid of Dirac impulses of varying magnitudes, spaced 1/s units apart ( s = sampling rate )
- analogous to an infinite two-dimensional grid of values
- feature map Z[x], sampling rate s
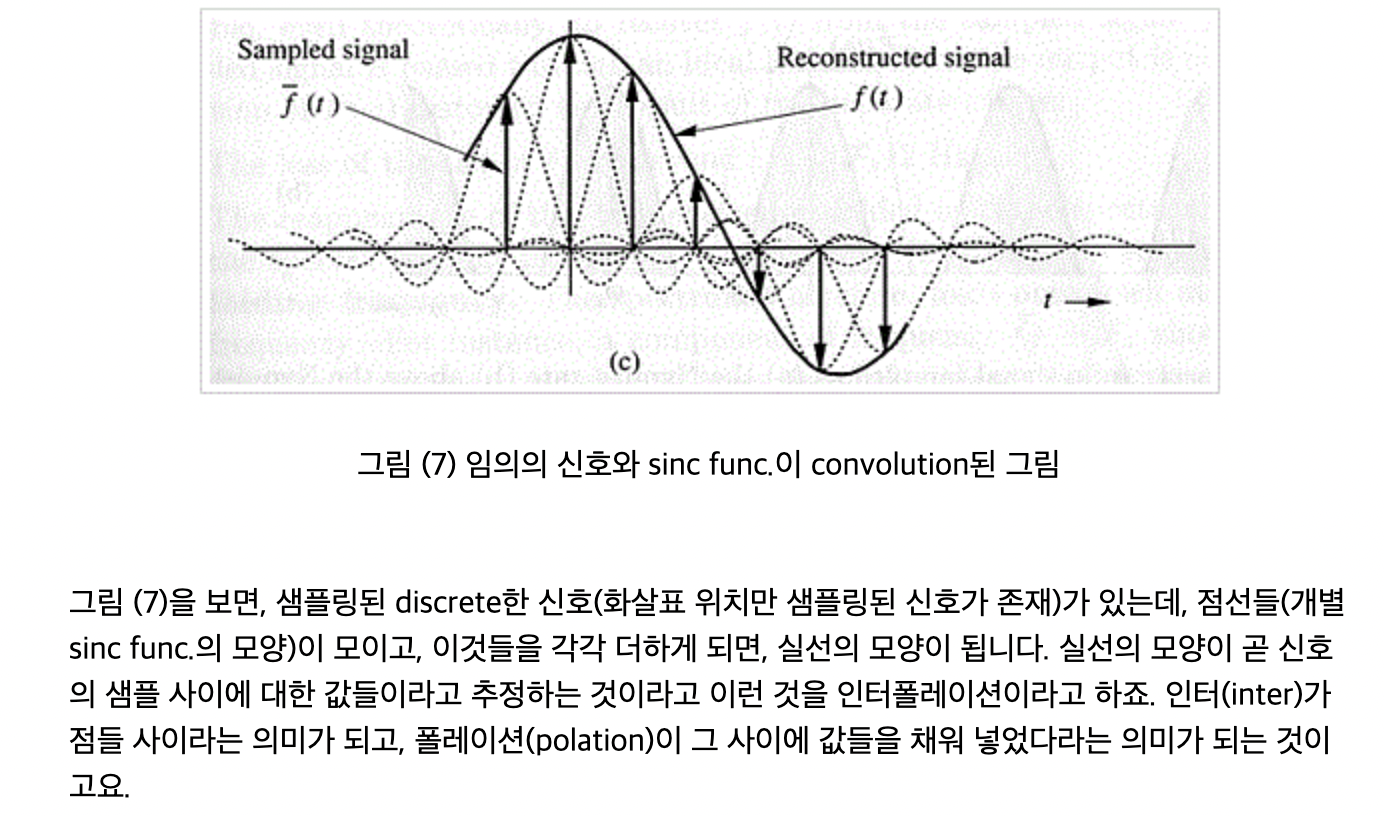
- Whittaker-Shannon 보간 공식(interpolation formula)
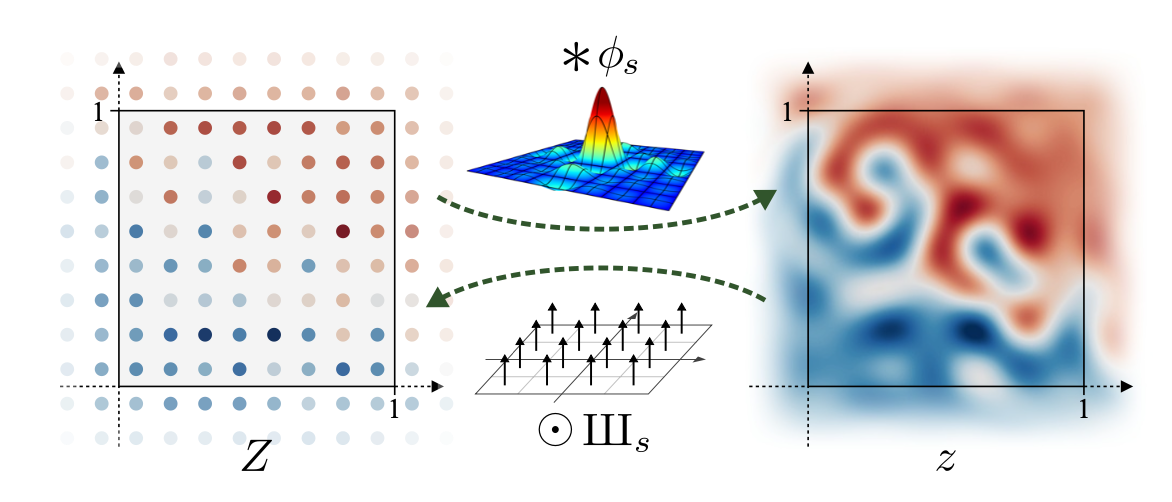
- 상응하는 연속적인 representation z(x) 는 불연속적으로 샘플된 Dirac grid Z[x] 와 ideal interpolation filter Øs 의 convolution으로 얻을 수 있음
- z(x) = ( Øs * Z )
- * : continuous convolution
- Øs(x) : sinc(sx0) · sinc(sx1)
- Øs : 수직축, 수평축을 따라 s/2 라는 bandlimit(대역제한)을 가짐 → 생성된 연속적인 신호가 sampling rate s로 표현되는 모든 주파수를 capture할 수 있음
- Whittaker-Shannon 보간 공식(interpolation formula)
- 연속적인 도메인에서 discrete한 도메인으로 전환하는 것 = 샘플링 포인트 Z[x]에서 연속적인 신호 z(x)를 샘플링하는 것
- “pixel centers”에 놓인(lie) 샘플 간격(sample spacing)의 절반으로써 상쇄되는 것
- 2차원 Dirac comb Шs(x) 로 pontwise multiplication으로 표현됨
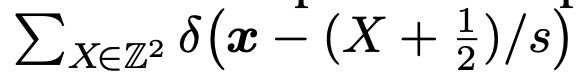
-
Discrete representation Z와 continuous representaion z 는 ideal interpolation 필터 Øs 의 convolution을 통해 서로 연관됨 - Dirac comb(Шs)의 pointwise multiplication
- z(x)에서 단위 정사각형(unit square) x ∈ [0, 1]2 을 관심 시그널(signal of interest)을 위한 캔버스(canvas)로 지정
- Z[x]에는 s2개의 불연속적인 sample이 있지만, 위의 Øs convolution은 단위 정사각형 밖의 Z[x] 값들이 그 안의 z(x)에 영향을 미칠 수 있음을 의미함. 따라서 s x s 사이즈의 픽셀 피처맵을 저장하는 것으로 충분하지 않음
- → 이론상 무한대의 Z[x] 전체를 저장해야 함
- → 실제적인 적용을 위하여, Z[x]를 단위 정사각형보다 살짝 큰 영역을 덮는 2차원 배열로 저장
- 대역폭이 제한된, 연속적인 피처맵 z(x)와 불연속적으로 샘플된 피처맵 Z[x] 간의 correspondence를 수립함으로써, 신호의 기존 pixel 중심 관점에서 멀어질 수 있음
- z(x)를 실제적인 신호로 해석하고 불연속적으로 샘플된 피처맵 Z[x]는 그것을 위한 편리한 인코딩으로만 해석할 것
Discrete and continuous representation of network layers
- 실제적으로 네트워크는 불연속적으로 샘플링된 피처맵에 작용
- 연산 F (convolution, nonlinearity, 등): 불연속적인 피처맵에 연산됨. Z' = F(Z)
- 피처맵은 상응하는 연속적인 counterpart가 있으므로, 연속적인 도메인에서 상응하는 맵핑이 존재함. z' = f(z)
- 한 도메인에서 명시된 연산은 다른 도메인에서도 그에 상응하는 연산으로 수행됨
- ◉ : pointwise multiplication
- s, s' : 입력과 출력의 sampling rate
- 중요: 후자의 f 는 출력 대역제한(output bandlimit) s'/2 이상의 주파수 내용(frequency content)을 들이지 않음

Equivariant network layers
- 연산 f 는 연속적인 도메인의 경우 2D 면의 spatial transformation(공간변환) t 에 있어서 equivariant 함
- 입력의 대역이 s/2로 제한될 때 equivariant한 연산은 출력 대역제한(output bandlimit) s'/2 이상의 주파수 내용을 생성해서는 안 됨 - 그렇지 않을 경우 faithful discrete output representation 이 존재하지 않는다
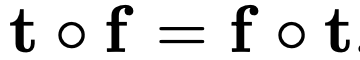
- 두 타입의 equivariance 에 주목: translation, rotation
- rotation 의 경우: spectral constraint가 더 엄격 - 회전하는 스펙트럼에 상응하도록 이미지를 회전시키는 것
- 수직, 수평 방향으로 bandlimit을 제한하기 위해서 스펙트럼은 반지름 s/2의 원으로 제한되어야 함
- 이는 초기 네트워크 입력 뿐만 아니라 downsampling에 사용하는 bandlimiting 필터들에도 적용되어야
- 생성기의 기초적인 연산들: convolution, upsampling, downsampling, nonlinearity
- generality의 손실 없이 하나의 피처맵에 작용하는 연산에 대해 논의: pointwise linear combination of features has no effect on the analysis

- rotation equivariance의 경우, 불연속적인 커널 K는 방사 대칭(radially symmetric)이어야 함
- 대칭적인 1x1 convolution 커널이 rotation equivariant한 생성 네트워크에 잘 적용됨


Nonlinearity
- 불연속 도메인에서 pointwise nonlinearity σ 를 적용하는 것은 fractional translation이나 rotation과 commute하지 않음
- 연속 도메인에서 모든 pointwise 함수는 자명하게 geometric transformation과 commute하므로, translation과 rotation에 equivariant 함
- 한편 bandlimit 제한(constraint)을 충족시키는 건 또다른 문제
- ReLU와 같은 함수를 연속적인 도메인에 적용하면, 출력에서 표현될 수 없는 높은 주파수가 임의로 개입될 수 있음

- 현재 수식에서 nonlinearity가 새로운 주파수를 생성할 수 있는 유일한 연산
- 최종 이산화 연산 전에 “s/2 보다 낮은 cutoff(차단)을 가진 reconstruction(복원) 필터”를 적용함으로써 이 새로운 주파수들의 범위를 제한할 수 있음
- 생성 네트워크의 각 레이어에서 얼마나 new information을 들일지 정확하게 통제할 수 있게 됨
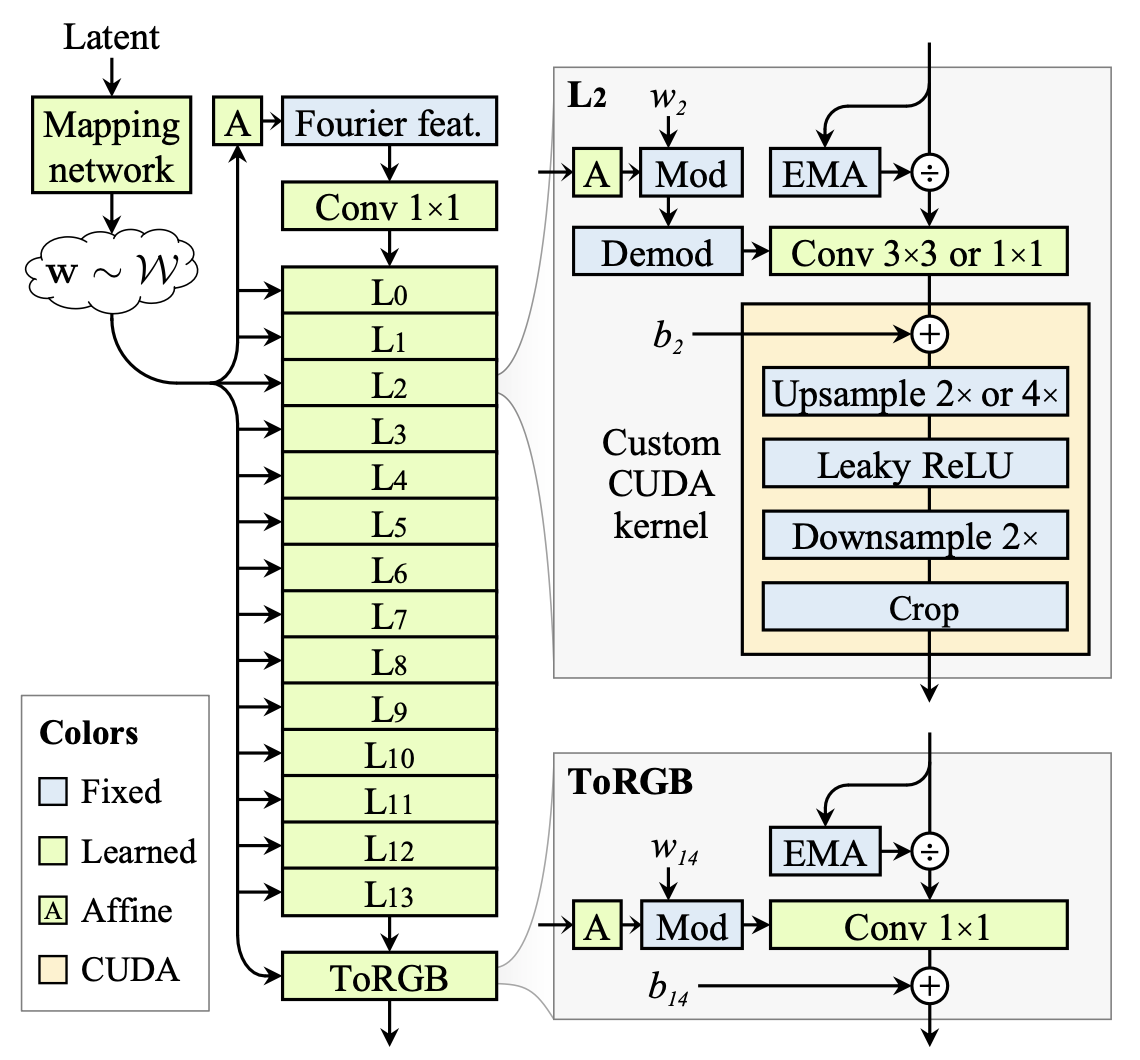
Practical application to generator network
- styleGAN2 생성기의 두 부분
- mapping network : 정규분포의 latent를 intermediate latent code w ~ W 로 변환
- synthesis network G : 학습된 4x4x512 사이즈의 상수 Z0에서 시작해 연속된 N개의 레이어에 적용 (convolutions, nonlinearites, upsampling, per-pixel noise), 출력 이미지 Zn = G(Z0; w)를 생성
- intermediate code w 는 convolution kernels 의 modulation을 통제함
- 레이어들은 rigid한 2x upsampling 스케줄을 따르는데, 두 개의 레이어는 각 해상도에서 실행되고 feature map의 개수는 각 upsampling 다음에 절반이 됨
- skip connections, mixing regularization, path length regularization
- 목표 : G의 모든 레이어가 연속적인 신호에 대해 equivariant 하도록 만들어서 모든 미세한(finer) 디테일들이 local neighborhood의 coarser feature들과 함께 변환되도록 하기
- 즉, 생성 네트워크의 연속적인 연산 g가 transformation t(translation and rotation)에 equivariant 하게 만들기 - transformation t는 연속적인 입력 z0에 적용됨
- z0의 변환 결과를 연속적으로 연산한 것 = z0; w의 연속적인 연산을 변환한 것
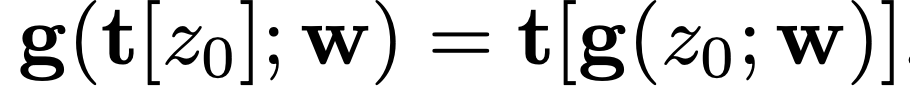
- 네트워크가 얼마나 equivariant한지 평가하는 지표 설정 (구체적인 내용 생략)
Fourier features and baseline simplifications (configs B-D)
- 입력 z0의 정확한 continuous translation & rotation을 도모하기 위해, 학습된 입력 상수를 Fourier features로 대체함 → 공간적으로 무한한 map을 자연스럽게 정의하는 이점이 있음
- band(대역) fc = 2 의 circular frequency 내에서 주파수들을 uniform하게 샘플링하여 기존 4x4 입력 해상도에 맞추고, 학습 과정에서 이를 고정시킴 → FID 지수가 살짝 개선되었으며 결정적으로 연산자 t를 근사하지 않고 equivariance metrics를 계산할 수 있음
- 베이스 아키텍처는 equivariant와 거리가 멂 (입력 feature가 변환되거나 원래 위치에서 회전할 경우 출력 이미지가 급격하게 악화되는 모습)
- 다음으로 per-pixel noise 입력을 제거함
- 자연스러운 transformation hierarchy라는 목표와 어울리지 않음; feature의 정확한 sub-pixel 위치가 오로지 기저의 coarse feature에서 내려와야 함(inherited)
- mapping network의 깊이를 줄이고, mixing regularization, path length regularization, output skip connection을 없음
- 이들의 이점이 대부분 학습 과정 중 gradient magnitude dynamics와 관련된다고 봄
- 각 convolution 전에 simple normalization을 이용함으로써 문제를 직접 다루기로 함
- exponential moving average를 모든 픽셀과 피처맵에 걸쳐 추적해보고, feature map들을 아래 연산자로 나눔
- 효율성 제고를 위해 convolution weight에 division을 내장시킴(baked into)
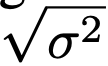
Boundaries and upsampling (config E)
- 이론상 feature map의 무한대 공간적 범위를 가정 - target canvas 의 가장자리(고정된 크기)를 유지함으로써 근사, 각 레이어를 지나서 이 확장된 canvas로 크롭함
- 이 extended canvas가 필수적인 이유 : border padding이 이미지의 절대 좌표를 internel representation에 유출시킴
- 10-pixel margin으로 충분했음
- ideal low-pass filter의 better approximation으로 bilinear 2x upsampling filter를 대체
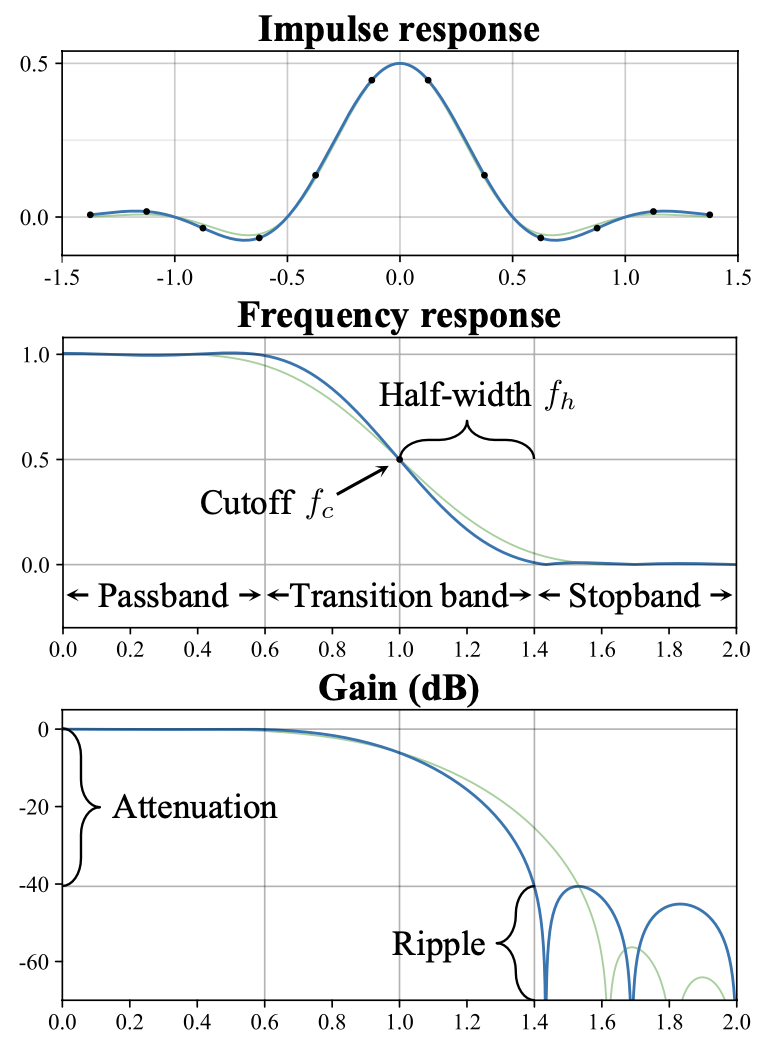
- 상대적으로 큰 Kaiser window (size n = 6) 의 windowed sinc filter를 사용
- 각 출력 픽셀이 upsampling에서 6개의 입력 픽셀에 의해 영향 받고, 각 입력 필터가 downsampling에서 6개의 출력 픽셀에 영향을 미침
- Kaiser window가 좋은 이유는 transition band(변환 대역)와 attenuation(쇠약)에 있어서 명확하게 통제할 수 있기 때문
- critical sampling을 적용, filter cutoff(차단)을 fc = s/2 (exactly at the bandlimit)으로 맞춤
- sampling rate s 는 canvas의 너비와 일치함
Filtered nonlinearities (config F)
- 각 leaky ReLU를 mx upsampling과 mx downsampling 사이로 wrapping 할 필요가 있음 (magnification factor 확대계수 m)
- 대역제한된 신호로 인해 upsampling과 convolution의 순서를 바꿔야 함
- 기존 2x upsampling과 (nonlinearity와 연관되는) 이어지는 mx upsampling을 하나의 2mx upsampling으로 융합할 수 있음
- m=2 로 충분함; 제공되는 프레임워크로 upsample → leaky ReLU → downsample 시퀀스가 충분히 구현되지 않아 커스텀 CUDA 커널로 직접 구현하였다고 함
Non-critical sampling (config G)
- filter cutoff를 정확하게 대역제한에 맞추는 샘플링 전략이 많은 이미지 처리에서 이상적임 - antialiasing과 고주파 디테일 보존 사이 균형을 맞출 수 있으므로
- 그러나 우리 목표는 이와 뚜렷하게 다른데, aliasing이 생성기의 equivariance에 매우 해롭기 때문
- 고주파 디테일들이 출력 이미지와 해상도가 높은 레이어들에서 중요한 요소인 한편, 앞선 레이어들에서는 덜 중요함; 정확한 해상도들로 시작하기에는 임의적인 면이 있다는 점에서(given that their exact resolutions are somewhat arbitrary to begin with)
- cutoff 주파수를 fc = s/2 - fh 로 낮춤으로써 aliasing을 억제할 수 있음
- 모든 alias frequency (s/2 이상)가 stopband(정지대역)에 있도록 하기 때문
- 예를 들어 파란색 필터의 cutoff 를 낮추면 주파수 반응이 왼쪽으로 이동하여 최악의 alias 주파수 attenuation가 6데시벨에서 40데시벨로 개선될 것
- 이러한 oversampling은 더 나은 antialiasing을 위한 computational 비용으로 볼 수 있는데, 전보다 더 천천히 변화하는(slower-varying) 신호를 표현하기 위해 동일한 개수의 샘플을 사용하기 때문
- 해상도가 가장 높은 레이어들을 제외하고 모든 레이어에서 fc를 낮춤 - 결국에 생성기는 학습 데이터와 match하는 crisp images를 생성해야 하기 때문
- 이제 신호들에 공간적 정보가 덜 포함되어 있으므로, feature map의 개수를 결정하는 데 사용한 heuristic을 수정하여 sampling rate s 대신에 fc에 반비례 하도록 만듦
Transformed Fourier features (config H)
- equivariant한 생성기 레이어들은 aligned되어 있지 않고 arbitrarily oriented한 데이터셋을 모델링하는 데 적합
- intermediate features zi에 도입되는 어떤 geometric transformation도 최종 이미지 zn으로 직접 넘어감
- 그러나, 레이어들이 스스로 전역적인(global) transformation을 도입하는 능력이 제한적이기 때문에, 입력 feature z0 은 zn의 전역적인 방향을 정의하는 데 중요한 역할을 함
- 이미지별로 방향이 달라지도록 하기 위해, 생성기는 w를 기반으로 z0를 변환시킬 수 있어야 함 → 학습된 affine 레이어 도입
- 입력 Fourier features를 위한 전역적 translation & rotation 파라미터를 출력함
- identity transformation을 수행하도록 초기화되지만 오랜 시간에 걸쳐(over time) 메카니즘을 사용하도록 학습됨
Flexible layer specifications (config T)
- 여전히 관찰되는 artifact → config G에서 정의된 filter의 attenuation 이 낮은 해상도 레이어에서는 불충분
- 이들 레이어는 대역제한 근처에서 풍부한 주파수 내용을 가지는 경향이 있음
- 이에 aliasing을 완전히 제거할 수 있는 매우 강력한 attenuation이 요구됨
- 지금까지는 StyleGAN2의 rigid한 sampling rate progression을 사용해왔음 + filter cutoff fc 와 절반 너비의 fh 를 위해 간소한 세팅(simplistic choices)
- 이렇게 하지 않아도 됨; layer별로 파라미터들을 specialize해도 된다
- 특히 fh를 낮은 해상도 레이어에서 높임으로써 stopband에서 attenuation을 극대화하고, 높은 해상도 레이어에서는 낮춤으로써 학습 데이터의 고주파 디테일에 맞출 수 있도록 함
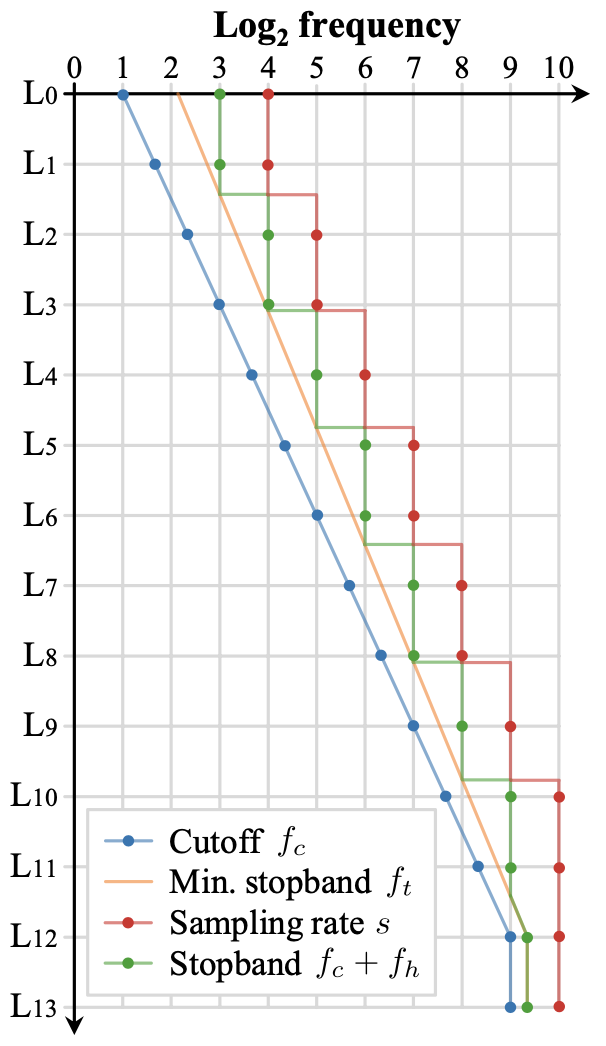
- 14개 레이어로 이루어져, 마지막에는 critically sampled full-resolution layer 두 개가 있는 생성기의 filter parameter progression
-
- cutoff 주파수는 첫번째 레이어에서 fc =2 였다가 기하학적으로(geometrically) 증가하여 첫번째 critically sampled layer에서 fc = sN/2가 됨
- 최소 수용가능(minimum acceptable) stopband 주파수는 ft,0 = 22.1에서 시작하여 기하학적으로 증가하게 함; 이때 cutoff 주파수보다는 천천히 증가
- 마지막 레이어에서 stopband 타겟은 ft = fc · 20.3 이지만, progression 는 첫번째 critically sampled 레이어에서 멈춤
- 다음으로, sampling rate s 를 각 레이어마다 세팅하여 ft까지 주파수를 accomodate할 수 있게 함; rounding up to the next power of two without exceeding the output resolution
- 마지막으로, aliasing frequencies의 attenuation을 최대화하여 transition 대역 절반 너비(band half-width)를 fh = max(s/2, ft) - fc 로 세팅, 즉 sampling rate의 한계 내에서 제일 넓게 만들면서, 최소한 ft에 이를 정도로 넓게 함
- ft 와 s/2 사이에 얼마나 slack(느슨한 부분)이 남는지에 resulting improvement가 달렸다
- 새로운 레이어 specification은 남아있던 artifacts를 제거하고 translation equivariance를 개선함
- 이제 레이어 개수는 출력 해상도에 직접 의존하지 않아 free parameter가 됨; 고정된 N이 여러 해상도에 걸쳐 일관적으로 작동하며 learning rate와 같은 다른 하이퍼파라미터도 예측가능하게 만들 수 있었음
- 본 논문에서 N = 14
Rotation equivariance (config R)
- 두 가지 변형을 통해 rotation equivariant한 네트워크를 만듦
- 첫번째, 모든 레이어에 있어서 3x3 convolution을 1x1 convolution으로 대체하고, 축소된 capacity는 feature map의 개수를 두 배로 늘림으로써 커버, upsampling & downsampling 연산만이 픽셀 간 정보(information between pixels)를 퍼뜨림
- 두번째, sinc-based downsampling 필터를 방사 대칭의 jinc-based 로 대체함 (동일한 Kaiser scheme으로 구성)
- 두 개의 critically sampled 레이어를 제외하고 모든 레이어에 적용하였으며, 학습 데이터의 potentially non-radial 스펙트럼을 맞추는 것이 중요
- 추가적인 안정화(stabilization) 작업
- 학습 초기에 식별기가 보는 모든 이미지를 가우시안 필터로 블러처리함
- σ = 10 픽셀로 시작해서 첫 200k장 동안 0으로 줄여나감
- 식별기가 초기에 고주파수에 너무 집중하는 것을 방지
- 이 작업이 없으면 초기에 collapse하기 쉬움 - 생성기가 살짝 딜레이된 채로 고주파수를 생성하도록 학습하고 식별기의 작업을 trivialize하기 때문
'인공지능 > computer vision' 카테고리의 다른 글
| ReStyle 이해하기 (0) | 2022.08.01 |
|---|---|
| p2S2p 이해하기 (0) | 2022.08.01 |
| styleGAN2 이해하기 (0) | 2022.05.31 |
| StyleGAN1 vs. StyleGAN2 (0) | 2022.05.31 |
| styleGAN 이해하기 (0) | 2022.05.31 |