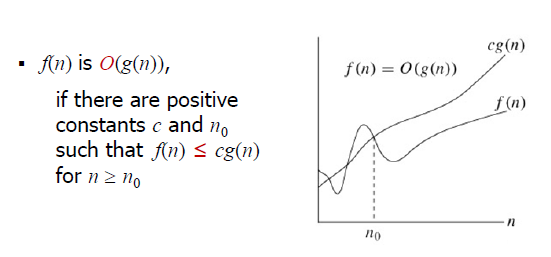
빅오표기법과 시간복잡도
정의
- 인수가 특정 값이나 무한으로 향할 때 함수의 극한 행위(limiting behavior)를 표현해주는 수학적 표기 -> 데이터가 늘어날 때 알고리즘 성능이 어떻게 바뀌는가?
- 알고리즘의 효율성을 상한선 기준으로 표기해준다 -> "최악의 시나리오"
복잡도

시간복잡도와 공간복잡도
- 시간복잡도 : 입력된 N의 크기에 따라 실행되는 조작의 수 ("데이터 원소가 N개일 때 알고리즘에 몇 단계가 필요한가")
- 공간복잡도 : 알고리즘이 실행될때 사용하는 메모리의 양
수학적 정의
$n \geq n_{0}$ 인 모든 $n$ 에 대해 $f(n) \leq cg(n)$ 인 양수 $c,\ n_{0}$ 가 존재한다면, $f(n)$ 을 $O(g(n))$ 이라고 나타낼 수 있다
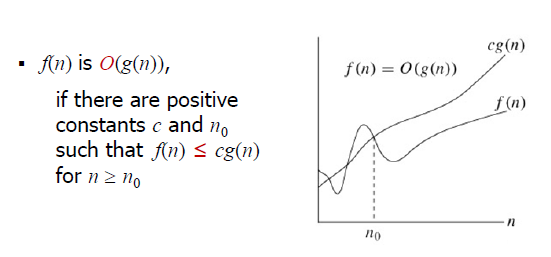
$n$은 $O(n)$로 나타낼 수 있다 - $n_{0}=1$, $c=1$ 이면 $n \leq n$ 이 만족되므로
$2n$은 $O(n)$로 나타낼 수 있다 - $n_{0}=1$, $c=2$ 이면 $2n \leq 2n$ 이 만족되므로
$n$은 $O(2n)$로 나타낼 수 있다- $n_{0}=1$, $c=\frac{1}{2}$ 이면 $n \leq \frac{1}{2} * 2n = n$ 이므로
$n$은 $O(n^{2})$로 나타낼 수 있다 - $n_{0}=1$, $c=1$ 이면 $n \leq n^{2}$ 이 만족되므로
$n^{2}$은 $O(n)$로 나타낼 수 없다 - $c$가 아무리 크더라도, 언젠가 항상 $cn$보다 $n^{2}$가 커지기 때문에, $n^{2} \leq cn$ 를 만족하는 $n_{0}$, $c$가 존재하지 않는다
$n^{2}$은 $O(n^{2})$는 맞음
$3n^{2}$ 역시 $O(n^{2})$가 됨
....
-> 빅오로 시간 복잡도를 표현할때는 최고차항만 표기힌다.
시간복잡도
규칙
1. $n \geq 0 $
입력값 $n$은 항상 $0$보다 크며, 복잡도 또한 $0$보다 크다고 가정한다
2. 함수는 더 많은 입력값이 있을 때 더 많은 작업을 한다
3. 모든 상수는 삭제한다
$n$, $2n$, $3n$ 모두 $O(n)$으로 표현할 수 있다
4. 낮은 차수의 항들은 무시한다
- $n$ 이 무한으로 커지는 경우를 상정한다
- $n^{3} + n^{2} +n$ 에서 시간 복잡도에 영향을 미치는 것은 $n^{3}$이다
5. $\log$의 밑은 무시한다
- 밑은 무시하고 $O(\log n)$ 으로 표시한다
6. 등호로 표현한다
- $2n = O(n)$ 및 $2n \in O(n)$
따라서 ...
| $1$ | $O(1)$ |
| $2n+20$ | $O(n)$ |
| $3n^{2}$ | $O(n^{2})$ |
이런 식이다.
종류
| 시간복잡도 | 1 | 10 | 100 | 문제 해결 단계 |
| $O(1)$ | 1 | 1 | 1 | 상수 시간 (문제 해결 시 오직 한 단계만 처리) |
| $O(\log n)$ | 0 | 2 | 5 | 로그 시간 (문제 해결에 필요한 단계들이 연산마다 특정 요인에 의해 줄어듦) |
| $O(n)$ | 1 | 10 | 100 | 직선적 시간 (문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐) |
| $O(n \log n)$ | 0 | 20 | 461 | 선형로그 시간 (문제를 해결하기 위한 단계의 수가 $n*(\log 2n)$ 번만큼의 수행시간을 가짐) |
| $O(n^{2})$ | 1 | 100 | 10000 | 2차 시간 (문제를 해결하기 위한 단계의 수는 입력값 n의 제곱) |
| $O(2^{n})$ | 2 | 1024 | 1267650600228229401496703205376 | 지수 시간 (문제를 해결하기 위한 단계의 수는 주어진 상수값 2 의 n 제곱) |
| $O(n!)$ | 1 | 3628800 | 표시 불가 |
예제
- O(1) : 상수
입력과 관계없이 시간복잡도 동일하게 유지됨
def hello():
print('hello, world!')
- O(N) : 선형
입력이 증가함에 따라 복잡도가 선형적으로 증가함
def print_each(data):
for item in data:
print(item)
- O(N^2) : Square
반복문이 겹쳐짐
def print_each_n_times(li):
for n in li:
for m in n:
print(n, m)
- O(log N), O(N log N)
입력 크기에 따라 처리시간 증가 ex. 정렬알고리즘
# 이진 검색
def binary_search(li, item, first=0, last=None):
if not last:
last = len(li)
midpoint = (last - first) / 2 + first
if li[midpoint] == item:
return midpoint
elif li[midpoint] > item:
return binary_search(li, item, first, midpoint)
else:
return binary_search(li, item, midpoint, last)
+ 정렬 알고리즘별, 자료구조별 시간 복잡도..
'컴퓨터 > 알고리즘&자료구조' 카테고리의 다른 글
| 최소 신장 트리 구하기 : 크루스칼(Kruskal) 알고리즘 (0) | 2022.10.05 |
|---|---|
| 합집합 찾기(union-find) (0) | 2022.10.05 |
| 자료구조 : 힙(heap) (0) | 2022.09.27 |
| 최단 경로 문제: 다익스트라 알고리즘 (0) | 2022.09.26 |
| 최단 경로 문제: 벨만포드 알고리즘 (1) | 2022.09.26 |