
Single View Geometry
사진만 보고 we can tell how we are oriented (어떤 물건 앞에 서 있고, 내려다 보고 있고 등등)
"geometry of scene"
3차원의 세계 (x, y, z) --> 2차원의 이미지 plane (two dimensional description of the world)
3번째 차원은 잃게 됨
how we orient ourselves to the world에 따라 그 지점에서의 이미지 project됨

How do wee see the word? how does the world refelct the geometry of the camera person himself?
3d simulation from single picture

사진으로부터 복도의 길이를 잴 수 있을까?
- unwarp (바닥의 타일 선이 평행이 되도록 만들기) 후 길이 재기
전제: 타일들이 평항하는 정사각형으로 이루어져 있다
또다른 아이디어: 소실점 vanishing points 이용하기 (infinity can be seen)

평행한 기둥들이 하나의 점으로 수렴하고 있음
오른쪽 지붕도 정면에서와 다르게 한 점으로 수렴함
--> 소실점
세상에는 많은 소실점이 있음. 그 소실점은 horizon 이라고 부르는 특정 선(소실선) 위에 있음
이를 통해 씬에 대한 카메라맨의 위치를 알 수 있음


line on ground plane 을 따라간다고 가정
물리 공간에서 포인트들은 수직으로 된 image plane 에 직선으로 project 되는데
물리적 공간에서 선을 따라 가면, image 공간에서는 선으로 투영되고,
멀어질수록 projection point들은 점점 거리가 좁혀지고 이내 하나의 점으로 수렴함 (infinity)
공간 세계에서는 서로 닿지 않는 라인이 많은데 image plane 에서는 모두 소실점에 수렴함
공간 세계에서 실제로 소실점을 볼 수 있는 것은 아님 - 대신에 투영된 선들이 교차하면서 물리적으로 하나의 점을 형성하는 것은 볼 수 있음
어쨌든 절대로 닿을 수 없는 점인데, 사진에는 물리적으로 존재함
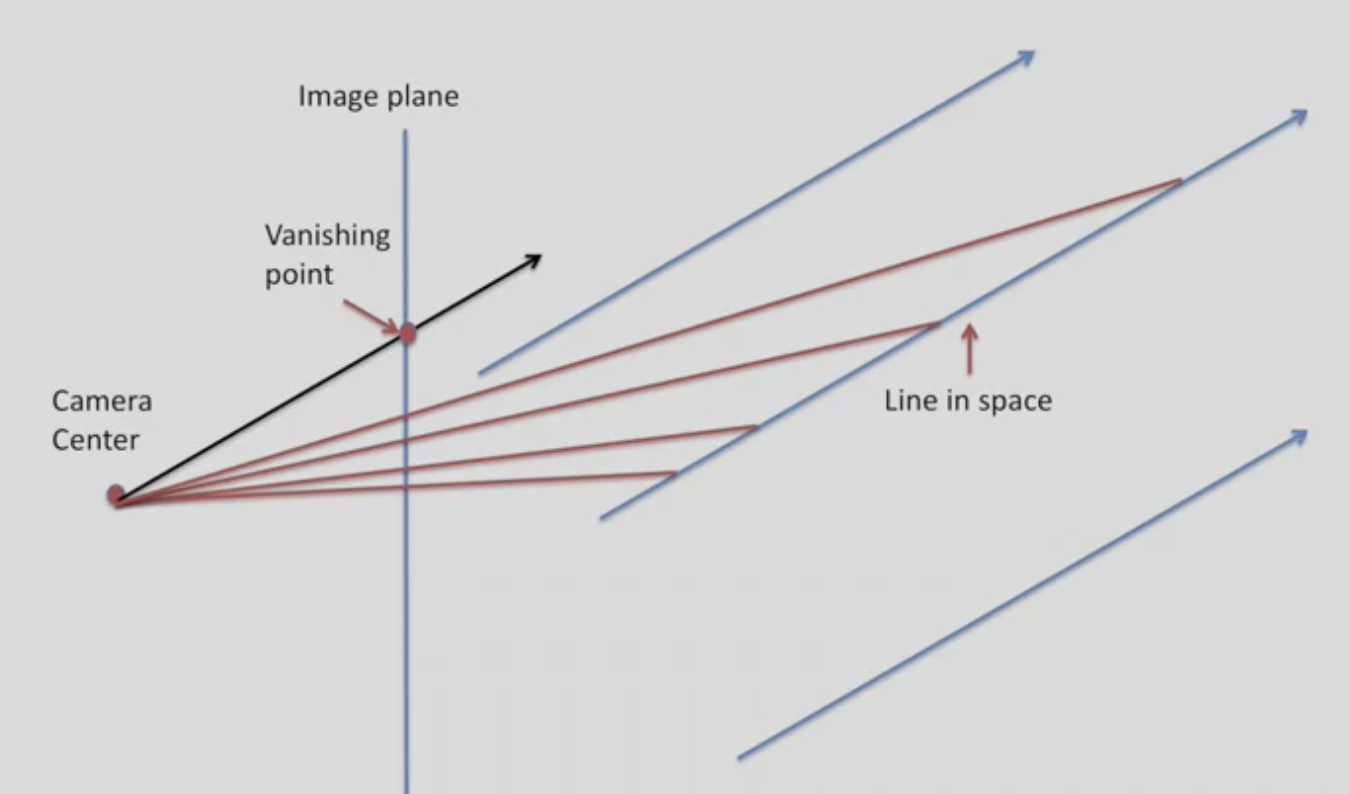
question : image plane 에서 평행으로 보이는 선들은 ground plane에서는 어떻게 보일까?

ground plane 에 선들이 있고, 그것들을 촬영했을 때 image plane 에서 수평한다고 가정
More on Perspective Projection

ground pllane 에 수직인 image plane 있다고 가정
P : original figure
O* : projection center (카메라나 사람의 눈의 위치)
P* : image plane에 그리는 것
O* 를 S점에 project 한다
O*S 길이(즉, 높이) 와 동일하게 하여 ground plane 에 O점을 찍는다 (O*S = OS)
OS는 카메라의 높이를 나타내줌
O와 P를 연결하는 선이 image plane과 만나나는 점을 M이라고 함
삼각형 O*SO가 등변직각삼각형이기 때문에 P*LM도 등변직각삼각형임
P*LM를 ground plane에 그대로 눕힐 수 있음
image plane의 P* 과 ground plane 에 누운 P* 은 동일하게 이동할 것임

현실의 동그라미를 그리려고 한다. 현실의 동그라미를 대각선으로 보면(obliquely) 동그라미는 타원형으로 보인다.
image plane 에 나타냈을 때 빨간 타원형이 나타나는 모습
조종할 수 있는 두 개 파라미터 - 카메라 높이와 focal length
O* : 카메라를 얼마나 높게 할 건지 (카메라는 아래로 내려갈수록 더 타원형으로 보일 것임)
image plane 과 O* 의 거리 (두 수직선의 거리) = focal length (이미지의 모양은 바뀌지 않고 크기가 달라짐)
'인공지능 > pose estimation' 카테고리의 다른 글
| Rotations and Translations (0) | 2022.05.09 |
|---|---|
| Point-line Duality (0) | 2022.05.09 |
| Perspective Projection (0) | 2022.05.06 |
| Glimpse on Vanishing Points (0) | 2022.05.06 |
| Camera modeling (0) | 2022.05.06 |