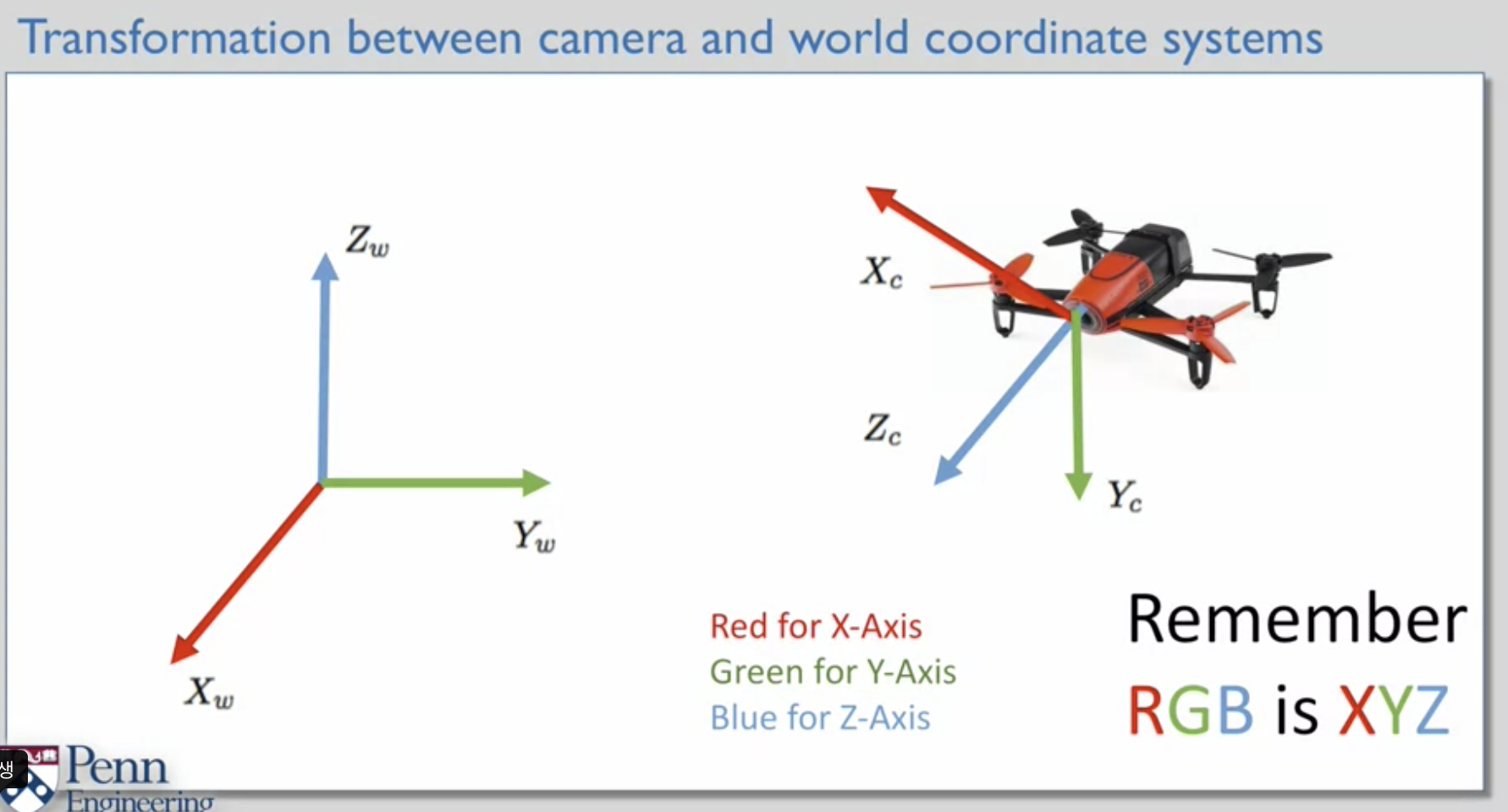
how to write "cooridnate transformations" built out of rotations, translations between thess two cooridnate systems

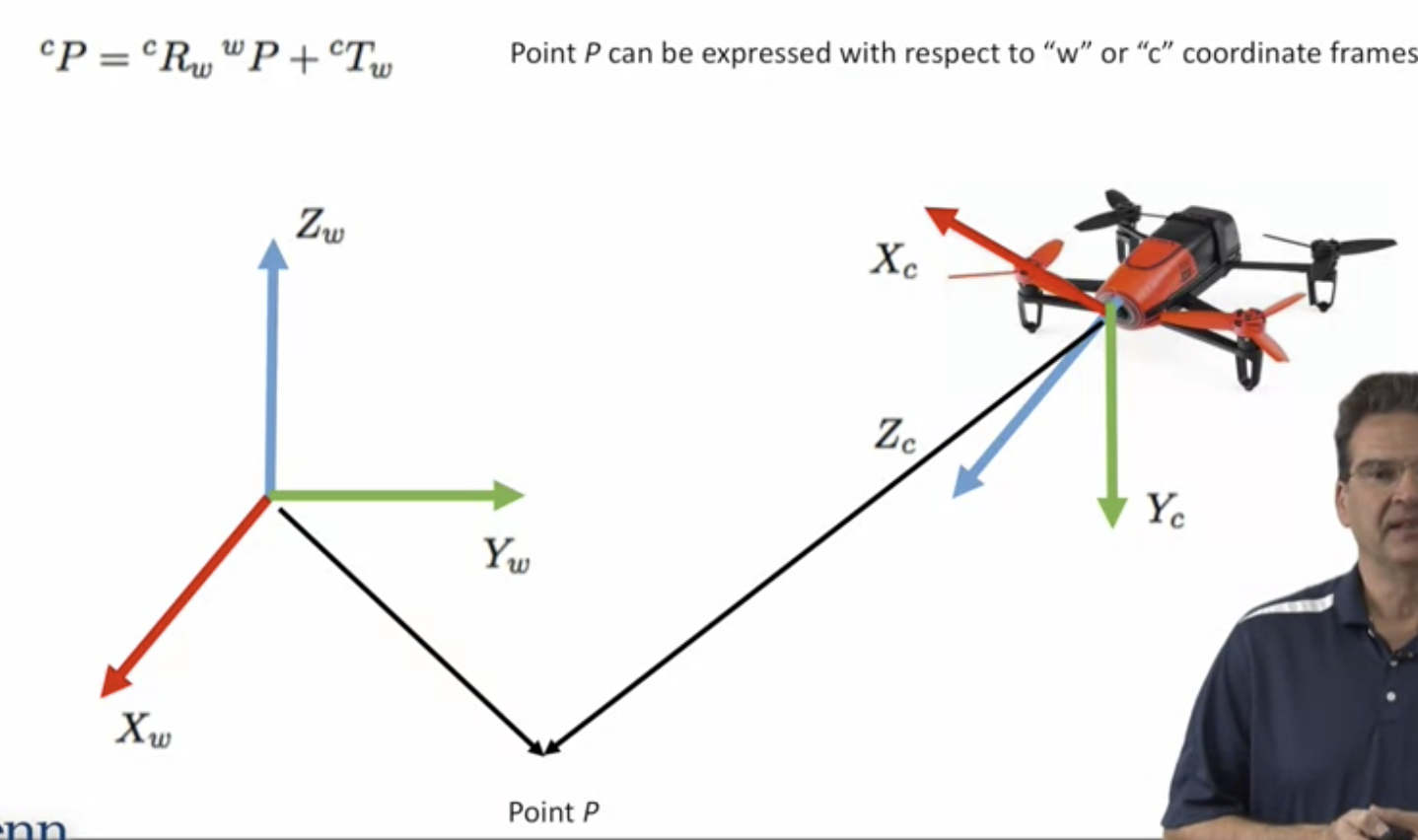
In computer vision, we project the points into image planes
we take a picture of the point with a camera
(1) the coordinates of the point in GPS - World Coordinates: wP (윗첨자)
(2) the coordinates of the point in the camera coordinate system - the ray that is going out from the projection centre and goes to the point : cP
rotation from the camera to world coordinate system
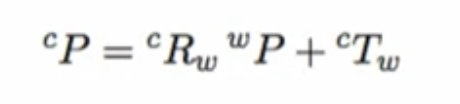
R: rotation / T : translation
[translation]
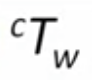
- 위 식에서 wP를 0으로 세팅하면, origin of the world 를 가지게 됨
- 벡터 cP는 camera 원점에서 시작해 world 원점으로 감
- cP = cTw, 즉 이 벡터값은 translation 과 동일하다
- 위 수식에 대해 이야기할 때, translation은 항상 from camera to world
[rotation]
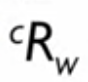
- rotation matric 은 세 개의 열 벡터로 표현되는 직교행렬
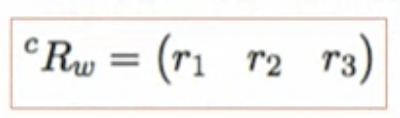
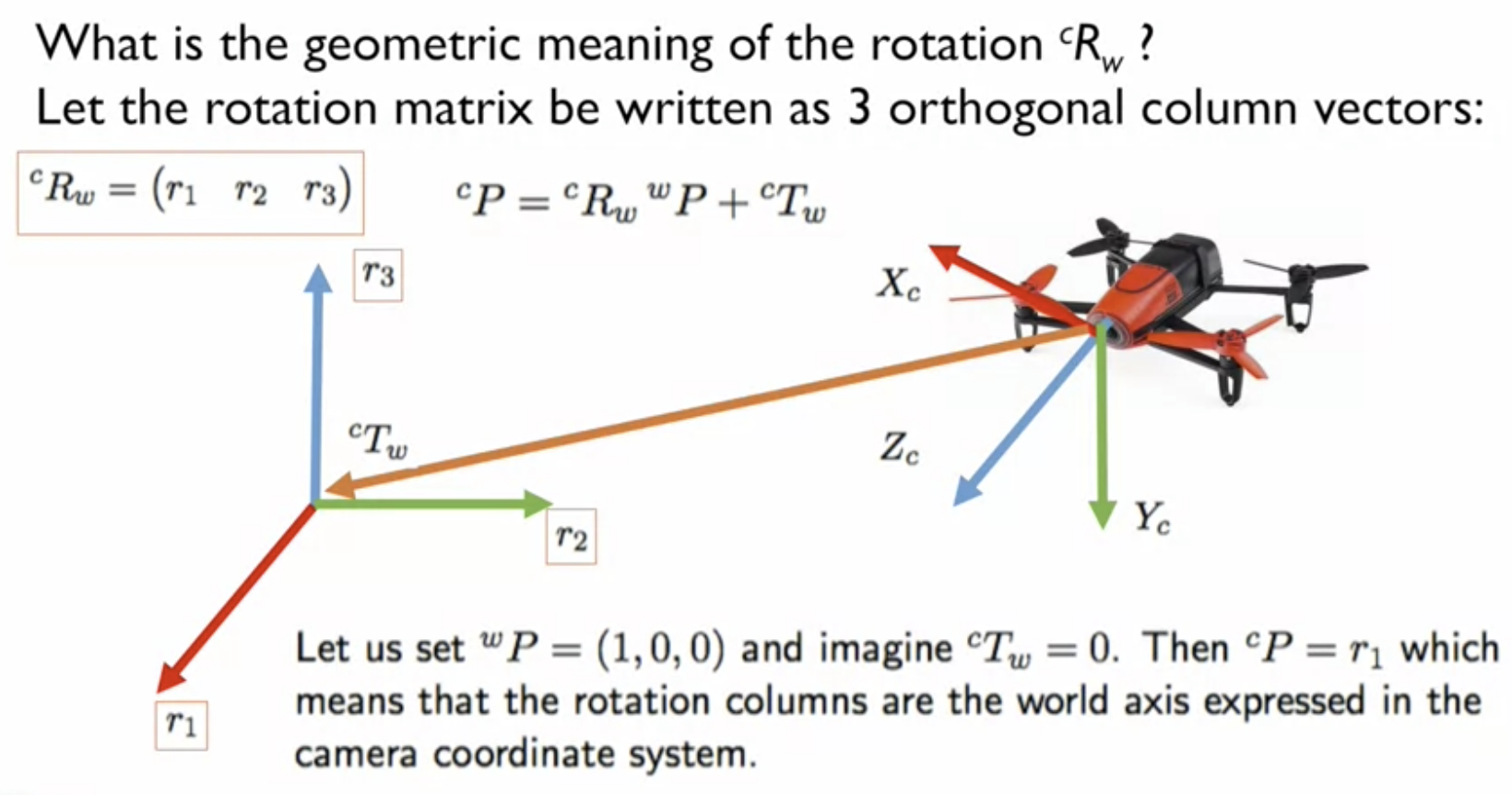
- translation을 0으로, wP 를 (1, 0, 0) 로 세팅하면 cP = r1
---> wP 가 (1, 0, 0) 이라는 것은?
- r1 : camera에 대한 world의 x축 (R)
- r2 : camera에 대한 world의 y축 (G)
- r3 : camera에 대한 world의 z축 (B)
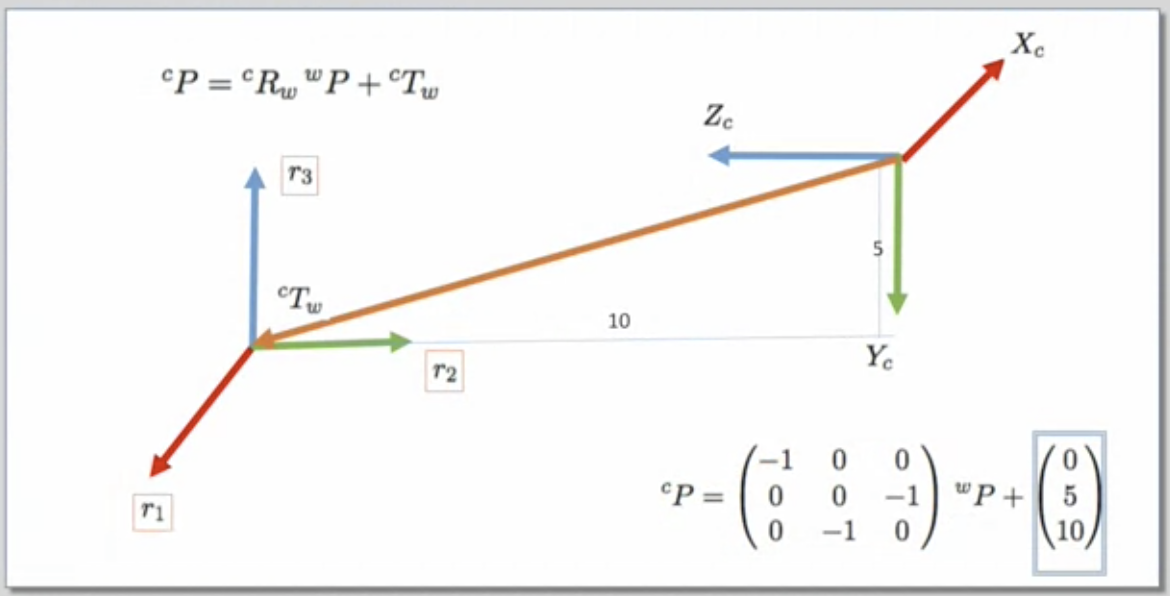
- 빨강색 x 축 주목 (카메라는 화면 안으로 들어가고 있는 것이고 월드는 화면 밖으로 (우리를 향해서) 나오고 있는 것임)
- camera에 대한 world의 x축은 무엇일까? 두 빨간 축은 반대 방향으로 평행한다
--> r1 은 (-1, 0, 0) 이다
- 두번째 열은 z축과 반대 방향으로 평행한다
--> (0, 0, -1)
- 세번째 열, 즉 camera에 대한 wolrd의 파란색 선은? 카메라의 초록선과 반대 방향으로 평행하므로
--> (0, -1, 0)
이를 통해 rotation from the world to the camera를 구할 수 있다
translation은? camera의 원점에서 world의 원점으로 가는 벡터다.
위 이미지에서는 yz plain에 있으므로 x 요소는 0, y 방향으로 5, z 방향으로 10
rotation 행렬은 항상 special orthogonal (특수 직교)이다

- 벡터끼리 서로 직교하면서
- determinant(행렬식)은 1에 해당한다
--> right handed coordinate system으로 작업하고 있는지 보기 위해 꼭 확이니해야 할 절차
[inverse transformation]
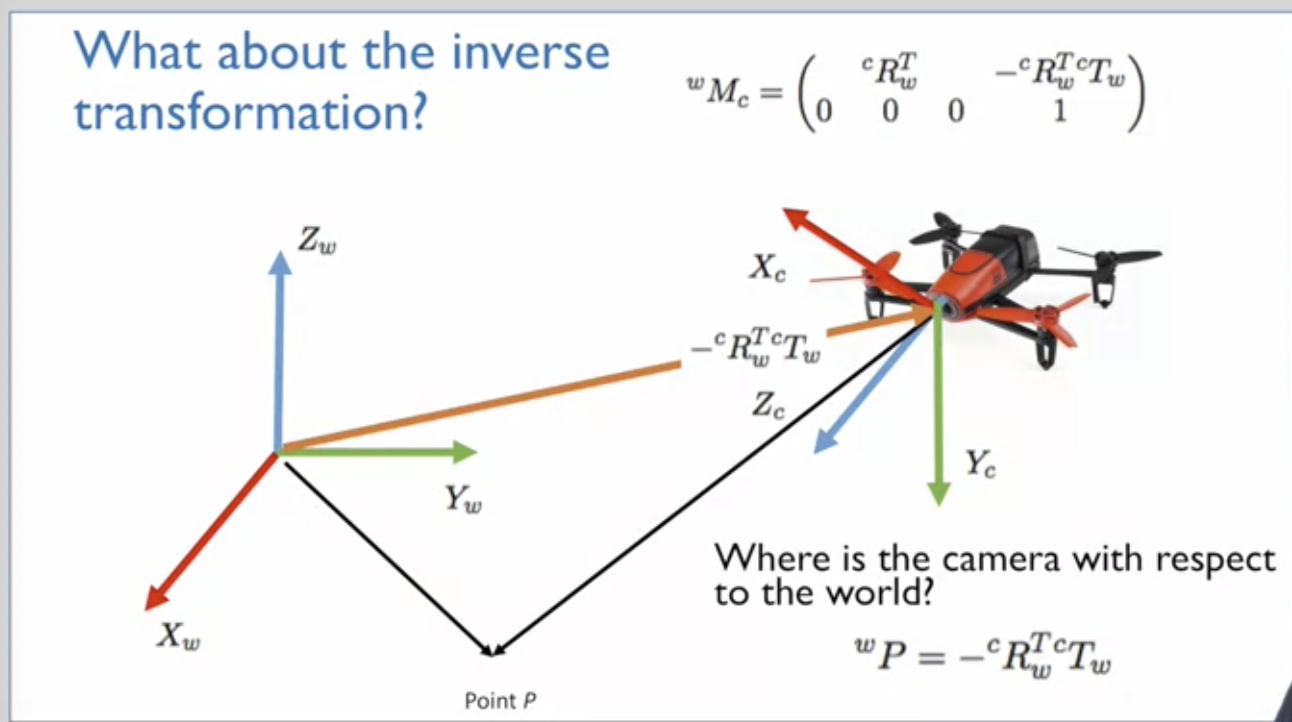
- inverse transformation : from the world 원점 to the camera 원점
- inverse of a rotation matrix = rotation matrix transposed
- inverse translation은? 4x4 행렬의 역행렬을 찾는다 (주황색 벡터)
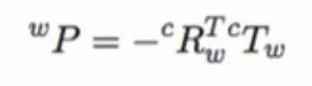
- world에 대해서 camera가 어디에 있는지를 찾을 수 있음
[transformation 다른 방식?]
- 좌표계 자체를 rotate하고 translate 하는 방법도 있음
(1) camera 좌표계를 world 좌표계 위에 겹친다
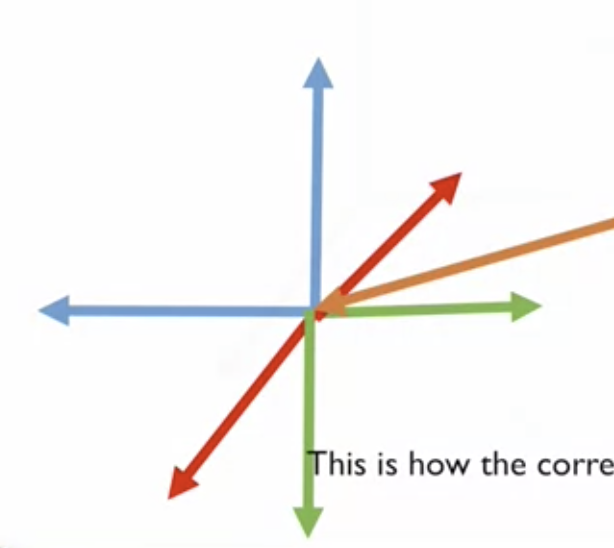
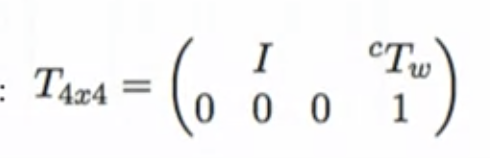
- rotation이 없기 때문에 T4x4에 I 를 기입
- 마지막 열에 translation vector 있음
(2) x축을 중심으로 -90도 회전한다
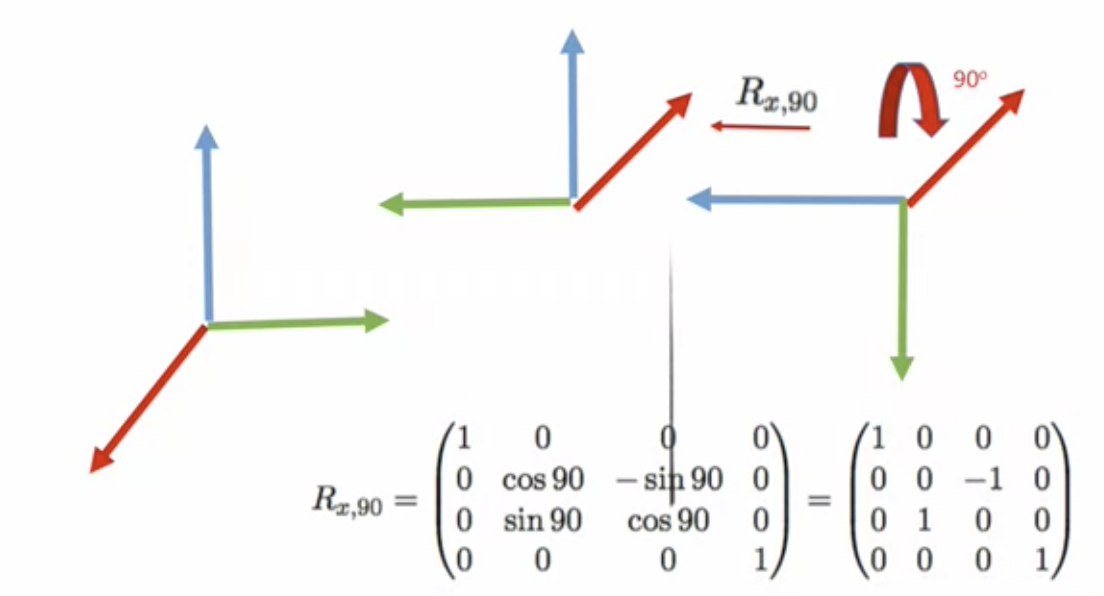
- 여기까지 Z축은 맞춰졌지만 나머지는 그렇지 않음 (z축 중심으로 180도는 돌아야 함)
(3) z축을 중심으로 180도 회전한다
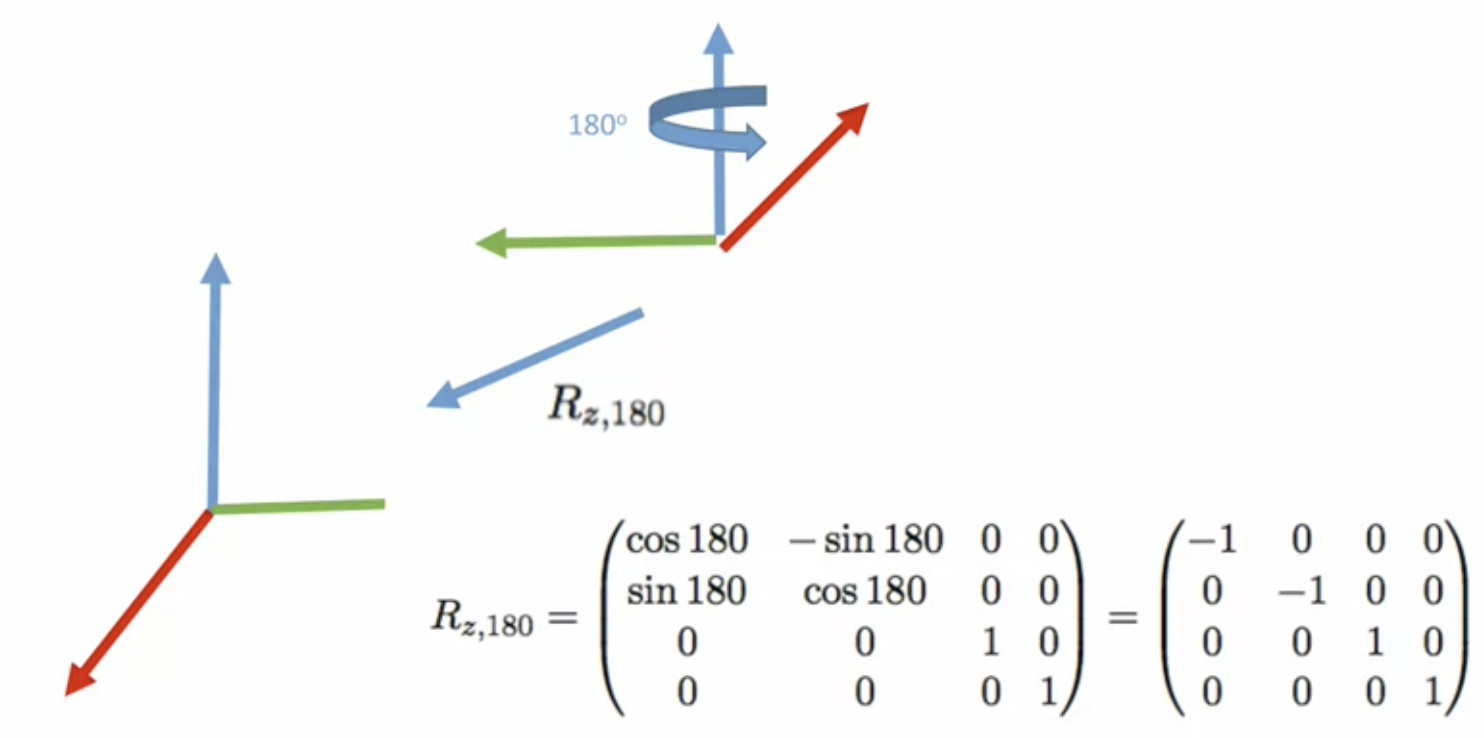
--> 즉 한번의 translation과 두번의 rotation이 있었음
"How do we compose these motions? Golen rule: when we move coordinate frames and we refer to the most recent coordinate frame we always postmultiply"

동일한 결과 나오는 것을 볼 수 있음

'인공지능 > pose estimation' 카테고리의 다른 글
| 3D World to First Person Transformation (0) | 2022.05.10 |
|---|---|
| Pinhole Camera Model/Focal Length and Dolly Zoom Effect/Intrinsic Camera Parameter (0) | 2022.05.10 |
| Point-line Duality (0) | 2022.05.09 |
| Perspective Projection (0) | 2022.05.06 |
| Glimpse on Vanishing Points (0) | 2022.05.06 |